လက်ဖြင့်တွဲထားသော t test ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။
နမူနာတစ်ခုတွင် ရှုမြင်မှု တစ်ခုစီရှိ အခြားနမူနာတစ်ခုရှိ စူးစမ်းမှုတစ်ခုနှင့် ဆက်စပ်နိုင်သောအခါ နမူနာနှစ်ခု၏နည်းလမ်းကို နှိုင်းယှဉ်ရန် တွဲထားသောနမူနာကို t-test ကို အသုံးပြုသည်။
အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာတွင် လူဦးရေဆိုသည်မှာ အောက်ပါအုပ်စုနှစ်ခုကြားတွင် တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် တွဲထားသော နမူနာ t-test ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-
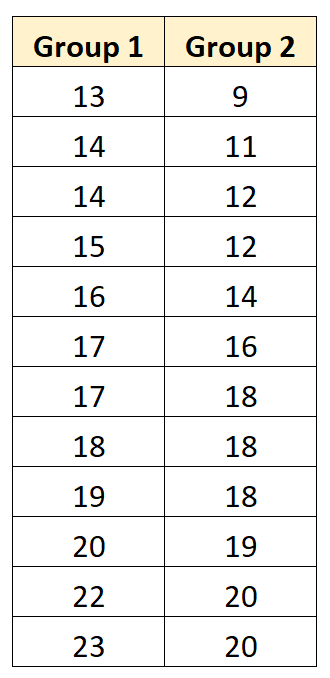
အဆင့် 1- စမ်းသပ်စာရင်းအင်းကို တွက်ချက်ပါ။
တွဲထားသော t-test ၏ စမ်းသပ်မှုစာရင်းကို အောက်ပါအတိုင်း တွက်ချက်သည်-
t = x diff / (s diff /√ n )
ရွှေ-
- x diff : ပျမ်းမျှကွဲပြားမှုများ၏ ဥပမာ
- s- စံသွေဖည်ကွဲပြားမှုများ၏ ဥပမာ
- n- နမူနာအရွယ်အစား (ဆိုလိုသည်မှာ အတွဲအရေအတွက်)
အုပ်စုနှစ်ခုကြားရှိ ခြားနားချက်များ၏ ပျမ်းမျှနှင့် အုပ်စုနှစ်ခုကြားရှိ ကွာခြားချက်များ၏ စံသွေဖည်မှုကို တွက်ချက်ပါမည်။
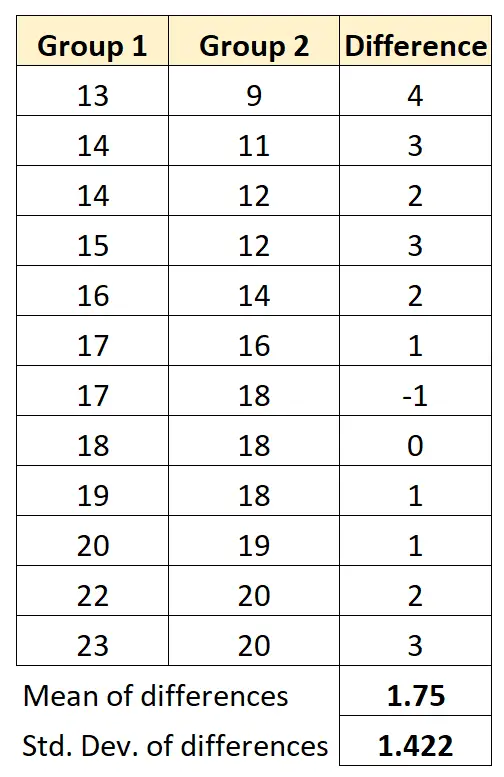
ထို့ကြောင့် ကျွန်ုပ်တို့၏ စမ်းသပ်စာရင်းအင်းအား အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။
- t = x diff / (s diff /√ n )
- t = 1.75 / (1.422/√ 12 )
- t = 4.26
အဆင့် 2- အရေးကြီးသောတန်ဖိုးကို တွက်ချက်ပါ။
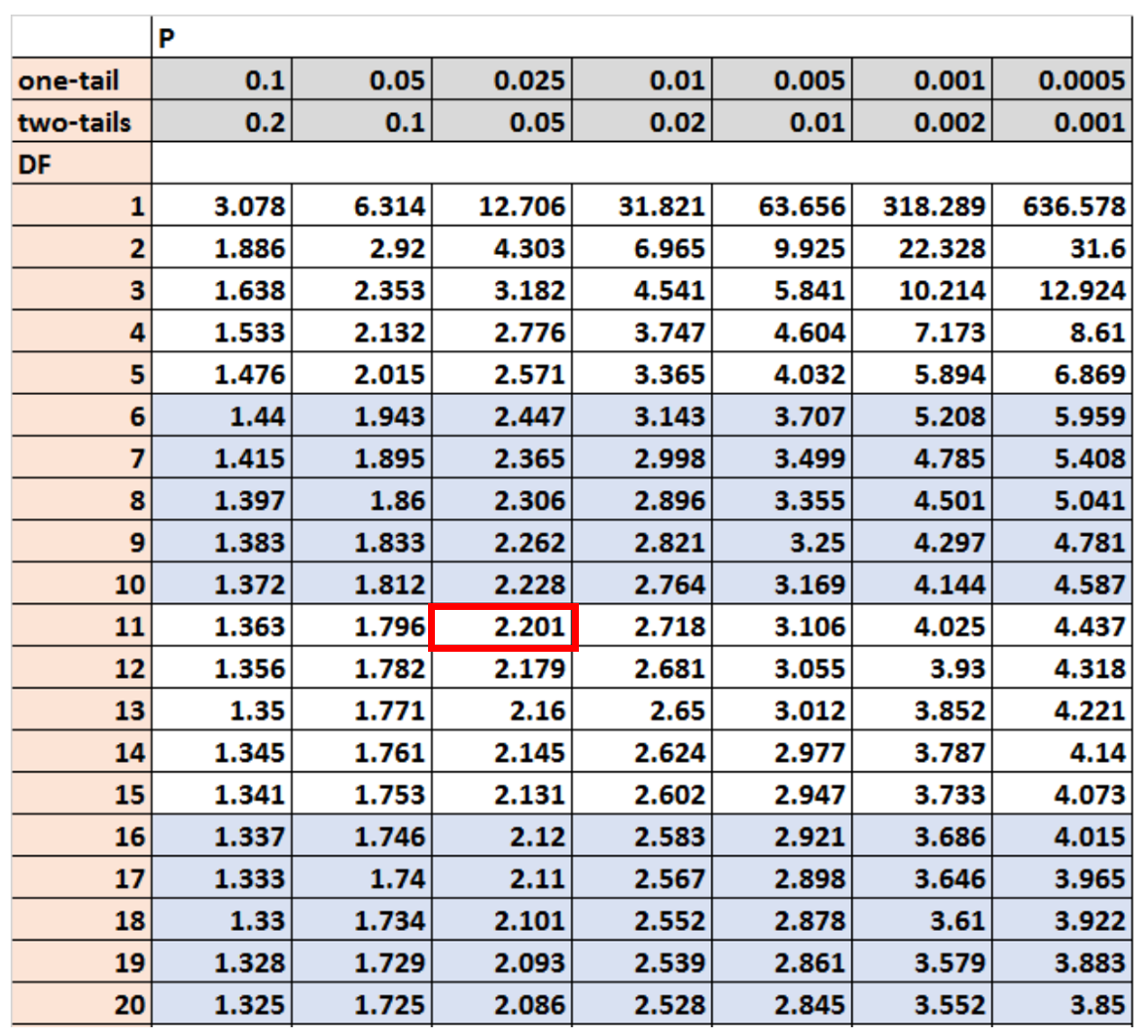
ထို့နောက်၊ ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းအင်းများနှင့် နှိုင်းယှဉ်ရန် အရေးကြီးသောတန်ဖိုးကို ရှာဖွေရန် လိုအပ်ပါသည်။
ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် လွတ်လပ်မှု α = 0.05 နှင့် df = n-1 ဒီဂရီဖြင့် အမြီးနှစ်ကြောင်းစမ်းသပ်မှုကို အသုံးပြုပါမည်။
t ဖြန့်ဖြူးမှုဇယားအရ၊ ဤတန်ဖိုးများနှင့် သက်ဆိုင်သည့် အရေးကြီးသောတန်ဖိုးမှာ 2.201 ဖြစ်သည် ။
အဆင့် 3- null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ပျက်ကွက်ခြင်း
ကျွန်ုပ်တို့၏တွဲစပ်ထားသောနမူနာ t-test သည် အောက်ပါ null နှင့် အခြားယူဆချက်အား အသုံးပြုသည်-
- H 0 : μ 1 = μ 2 (လူဦးရေ နှစ်ခုသည် တူညီသည်)
- H A : μ 1 ≠ μ 2 (လူဦးရေ နှစ်ခု အဓိပ္ပါယ်မှာ မညီမျှခြင်း)
ကျွန်ုပ်တို့၏စမ်းသပ်စာရင်းအင်း၏ ပကတိတန်ဖိုး ( 4.26 ) သည် t-table ( 2.201 ) တွင်တွေ့ရှိရသော အရေးကြီးသောတန်ဖိုးထက် ကြီးသောကြောင့် ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။
ဆိုလိုသည်မှာ အုပ်စုနှစ်ခုကြား ပျမ်းမျှ ညီမျှခြင်း မရှိဟု ဆိုရန် လုံလောက်သော သက်သေ အထောက်အထားများ ကျွန်ုပ်တို့တွင် ရှိသည်ဟု ဆိုလိုပါသည်။
အပိုဆု- သင်၏ရလဒ်များကိုအတည်ပြုရန် တွဲထားသောနမူနာများကို t-test calculator ကို အသုံးပြုရန် အားမနာပါနှင့်။