လူဦးရေဆိုသည်မှာ

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားတွင် လူဦးရေ၏အဓိပ္ပါယ်ကို ရှင်းပြထားသည်။ အလားတူပင်၊ လူဦးရေအတွက် ဖော်မြူလာဟူသည် အဘယ်နည်း၊ လူဦးရေ၏ယုံကြည်မှုကြားကာလကို မည်ကဲ့သို့ တွက်ချက်သနည်း၊ ထို့အပြင်၊ လူဦးရေဆိုလိုသည်နှင့် နမူနာ၏ဆိုလိုအား ကွာခြားချက်မှာ အဘယ်နည်း။

လူဦးရေ ပျမ်းမျှ ဘယ်လောက်လဲ။

လူဦးရေ ပျမ်းမျှ သည် စာရင်းအင်းလူဦးရေ၏ ဒြပ်စင်အားလုံး၏ ဂဏန်းသင်္ချာပျမ်းမျှဖြစ်သည်။ ထို့ကြောင့် လူဦးရေဆိုလိုရင်းကို တွက်ချက်ရန်အတွက် လူဦးရေတန်ဖိုးအားလုံးကို ပေါင်းထည့်ကာ လူဦးရေရှိ ဒြပ်စင်အရေအတွက် စုစုပေါင်းဖြင့် ပိုင်းခြားရပါမည်။

လူဦးရေအတွက် သင်္ကေတသည် ဂရိအက္ခရာ µ ဖြစ်သည်။

အလားတူ လူဦးရေဆိုလိုရင်းကိုလည်း လူဦးရေကိုကိုယ်စားပြုသည့် variable ၏ မျှော်မှန်းတန်ဖိုး အဖြစ် သတ်မှတ်နိုင်သည်။

လူဦးရေ ပျမ်းမျှတွက်နည်း

လူဦးရေဆိုလိုရင်း၏ အဓိပ္ပါယ်ကို ကျွန်ုပ်တို့မြင်ပြီးသည်နှင့် ၎င်း၏အဓိပ္ပာယ်ကို ပိုမိုနားလည်ရန် လူဦးရေဆိုလိုသည် မည်ကဲ့သို့တွက်ချက်သည်ကို ကြည့်ကြပါစို့။

စာရင်းအင်းလူဦးရေရှိတန်ဖိုးအားလုံးကိုသိပါက၊ ဂဏန်းသင်္ချာဆိုလိုပုံသေနည်းသည် လူဦးရေဆိုလိုအားတွက်ချက်ရန် ရိုးရိုးရှင်းရှင်းအသုံးပြုသင့်သည်။ ထို့ကြောင့် ဤကိစ္စတွင်၊ လူဦးရေဆိုလိုရင်းကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် လူဦးရေတန်ဖိုးများအားလုံးကို ပေါင်းထည့်ကာ ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားရန် လိုအပ်ပါသည်။

ထို့ကြောင့် လူဦးရေ၏ဒြပ်စင်အားလုံး၏တန်ဖိုးကို သိပါက လူဦးရေဆိုလိုအား တွက်ချက်ရန် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ ဂဏန်းသင်္ချာပျမ်းမျှတွက်နည်းကို ကြည့်ပါ။

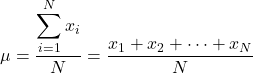
သို့သော်လည်း ယေဘုယျအားဖြင့် လူဦးရေတန်ဖိုးအားလုံးကို မသိရသောကြောင့် ပုံမှန်အားဖြင့် လူဦးရေ၏တန်ဖိုးကို ကြားကာလအားဖြင့် ခန့်မှန်းပါသည် ။

Confidence interval for population ကိုဆိုလိုသည်။

လက်တွေ့တွင်၊ လူဦးရေတစ်ခုစီရှိ လူအားလုံးကို လေ့လာရန် မဖြစ်နိုင်သောကြောင့် လူဦးရေ၏ ကျပန်းနမူနာကို သာမန်အားဖြင့် ရွေးချယ်ပြီး ၎င်း၏တန်ဖိုးများအပေါ် အခြေခံ၍ လူဦးရေ၏ ဆိုလိုရင်းတန်ဖိုးကို အနီးစပ်ဆုံးလုပ်ဆောင်သည်။ ပိုမိုတိကျစွာ၊ ကျွန်ုပ်တို့သည် လူဦးရေတစ်ရပ်လုံး၏ပျမ်းမျှအား လိမ်လည်ပြောဆိုနိုင်ဖွယ်ရှိသည့် ကြားကာလတစ်ခုကို တွက်ချက်ပါသည်။ ဤကြားကာလကို လူဦးရေအတွက် ယုံကြည်မှုကြားကာလဟု ခေါ်သည်။

လူဦးရေပျမ်းမျှအတွက် ယုံကြည်မှုကြားကာလကို နမူနာဆိုလိုရင်း Z _α/2 ၏တန်ဖိုးကို စံသွေဖည်မှု (σ) ဖြင့်မြှောက်ကာ နမူနာ (n) အမြင့်၏ နှစ်ထပ်ကိန်းအရင်းဖြင့် ပိုင်းခြားခြင်းဖြင့် တွက်ချက်သည်။ ထို့ကြောင့် လူဦးရေအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

လူဦးရေကွဲပြားမှုကို သိသောအခါ အထက်ဖော်ပြပါ ဖော်မြူလာကို အသုံးပြုသည်။ သို့သော်၊ လူဦးရေကွဲလွဲမှုကို မသိပါက၊ အဖြစ်များဆုံးကိစ္စဖြစ်သည့်၊ ဆိုလိုရင်းအတွက် ယုံကြည်မှုကြားကာလကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

ရွှေ-

$\overline{x}$

နမူနာဆိုလိုသည်။
$t_{\alpha/2}$

ဖြစ်နိုင်ခြေ α/2 ရှိသော လွတ်လပ်မှု n-1 ဒီဂရီ၏ ကျောင်းသား၏ t ဖြန့်ဖြူးမှုတန်ဖိုးဖြစ်သည်။ ကြီးမားသောနမူနာအရွယ်အစားများနှင့် 95% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 1.96 နှင့် နီးစပ်ပြီး 99% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 2.576 နှင့် နီးစပ်ပါသည်။
$s$

နမူနာစံသွေဖည်သည်။
$n$

နမူနာအရွယ်အစားဖြစ်သည်။

➤ ကြည့်ပါ- လူဦးရေအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ခြင်း ဥပမာ

လူဦးရေ ပျမ်းမျှနှင့် နမူနာဆိုလိုသည်။

နောက်ဆုံးအနေဖြင့် အချုပ်အားဖြင့်၊ လူဦးရေဆိုလိုရင်းနှင့် နမူနာဆိုလိုမှုအကြား ကွာခြားချက်များကို ပြန်လည်သုံးသပ်ပြီး ဤကိန်းဂဏန်းဆိုင်ရာ အယူအဆနှစ်ခုကို ရှင်းလင်းစေရန်။

လူဦးရေပျမ်းမျှနှင့် နမူနာဆိုလိုးကွာခြားချက် သည် ပျမ်းမျှတွက်ချက်ထားသည့် တန်ဖိုးများအကွာအဝေးဖြစ်သည်။ လူဦးရေပျမ်းမျှသည် စာရင်းအင်းလူဦးရေတစ်ခုလုံး၏ပျမ်းမျှဖြစ်ပြီး၊ နမူနာဆိုလိုသည်မှာ လူဦးရေနမူနာတစ်ခု၏ပျမ်းမျှဖြစ်သည်။

ထို့အပြင်၊ နမူနာဆိုလိုမှုမှ လူဦးရေကို ခွဲခြားရန်၊ ၎င်းတို့ကို သင်္ကေတအမျိုးမျိုးဖြင့် ကိုယ်စားပြုပါသည်။ လူဦးရေအတွက် သင်္ကေတဟူသည်

$\mu$

တစ်ဖက်တွင်၊ နမူနာအတွက် သင်္ကေတဟူသည် ဖြစ်၏။

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

အကယ်၍ သင်သည် ဤပျမ်းမျှအမျိုးအစားနှစ်ခုကြား ခြားနားချက်များကို သံသယရှိနေပါက သို့မဟုတ် နမူနာပျမ်းမျှတွက်ချက်ခြင်းအကြောင်း ပိုမိုသိရှိလိုပါက အောက်ပါဆောင်းပါးကို တိုင်ပင်နိုင်ပါသည်။

➤ ကြည့်ပါ- နမူနာဟူသည် အဘယ်နည်း။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။