ကွာတားများ
ဤဆောင်းပါးတွင် quartiles သည် အဘယ်အရာဖြစ်သည်ကို ရှင်းပြထားပါသည်။ Quartile တစ်ခုစီ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ၎င်းတို့ကို တွက်ချက်ပုံနှင့် ခိုင်မာသော ဥပမာများစွာကို သင်တွေ့လိမ့်မည်။ အုပ်စုဖွဲ့ဒေတာအတွက် quartiles တွက်ချက်နည်းကိုလည်း သင်ပြပေးပါသည်။ ထို့အပြင်၊ သင်သည် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် မည်သည့်ဒေတာအစု၏ လေးပုံတစ်ပုံကို တွက်ချက်နိုင်မည်ဖြစ်သည်။
Quartiles တွေက ဘာတွေလဲ။
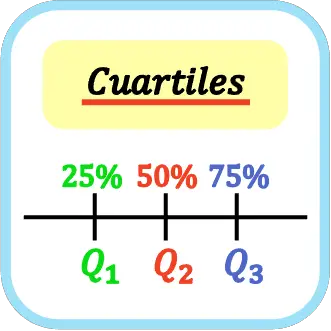
စာရင်းဇယားများတွင်၊ quartiles များသည် မှာယူထားသောဒေတာအစုအဝေးကို လေးပိုင်းအညီအမျှ ပိုင်းခြားပေးသည့် တန်ဖိုးသုံးခုဖြစ်သည်။ ထို့ကြောင့် ပထမ၊ ဒုတိယနှင့် တတိယ ကွာတားများသည် ကိန်းဂဏန်းအချက်အလက်အားလုံး၏ 25%, 50% နှင့် 75% အသီးသီး ကိုယ်စားပြုသည်။
Quartile များကို အရင်းအနှီး Q နှင့် quartile အညွှန်းကိန်းဖြင့် ကိုယ်စားပြုသည်၊ ထို့ကြောင့် ပထမ quartile သည် Q 1 ၊ ဒုတိယ quartile သည် Q 2 ဖြစ်ပြီး တတိယ quartile သည် Q 3 ဖြစ်သည်။
👉 မည်သည့်ဒေတာအစု၏ လေးပုံတစ်ပုံကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။
Quartiles များသည် quintiles၊ deciles နှင့် percentiles များကဲ့သို့ပင် ဗဟိုအနေအထားမဟုတ်သော အတိုင်းအတာတစ်ခုဖြစ်ကြောင်း သတိပြုသင့်သည်။ ဤပမာဏအမျိုးအစားတစ်ခုစီသည် ဤဝဘ်စာမျက်နှာတွင် မည်သည့်အရာဖြစ်သည်ကို သင်စစ်ဆေးနိုင်ပါသည်။
ပထမလေးပုံတစ်ပုံ
ပထမ quartile ၊ quartile 1 ဟုလည်းခေါ်သည်၊ သည် နမူနာတစ်ခုရှိ ကိန်းဂဏန်းအချက်အလက်များ၏ 25% ထက်ကြီးသောတန်ဖိုးဖြစ်သည်။ တစ်နည်းဆိုရသော် ပထမ quartile သည် လေ့လာတွေ့ရှိထားသော အချက်အလက်များ၏ 25% ကျော်ကို ကိုယ်စားပြုသည်။
ပထမ quartile ကို Q 1 သင်္ကေတဖြင့် ဖော်ပြပြီး နမူနာရှိ အသေးငယ်ဆုံးဒေတာတန်ဖိုးများကို ဖော်ပြရန်အတွက် အသုံးပြုသည်။
ဒုတိယ လေးပုံတစ်ပုံ
ဒုတိယ quartile ၊ quartile 2 ဟုခေါ်သော၊ သည် နမူနာတစ်ခုရှိ ကိန်းဂဏန်းအချက်အလက်များ၏ 50% ထက်ကြီးသောတန်ဖိုးဖြစ်သည်။ ထို့ကြောင့်၊ ဒုတိယ quartile သည် သတ်မှတ်ဒေတာကို နှစ်ပိုင်းခွဲကာ အလယ်အလတ်နှင့် ပဉ္စမ decile တို့နှင့် တိုက်ဆိုင်သည်။
ဒုတိယ quartile အတွက် သင်္ကေတသည် Q2 ဖြစ်သည်။
တတိယ ကွာတား
တတိယ quartile ၊ 3rd quartile ဟုခေါ်သော၊ သည် နမူနာတစ်ခုရှိ ကိန်းဂဏန်းအချက်အလက်များ၏ 75% ထက်ကျော်လွန်သောတန်ဖိုးဖြစ်သည်။ တစ်နည်းဆိုရသော် တတိယ ကွာတားသည် စုဆောင်းထားသော အချက်အလက်၏ 75% ကျော်ကို ကိုယ်စားပြုသည်။
တတိယ quartile ကို Q 3 သင်္ကေတဖြင့် ဖော်ပြပြီး နမူနာရှိ အကြီးဆုံးတန်ဖိုးများကို ကိုယ်စားပြုသည်။
လေးပုံတစ်ပုံတွက်နည်း
ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ quartiles များ၏ အနေအထားကို တွက်ချက် ရန်၊ သင်သည် ဒေတာစုစုပေါင်းအရေအတွက်၏ ပေါင်းလဒ်နှင့် quartiles များကို မြှောက်ပြီး ရလဒ်ကို လေးခုခွဲရမည်။
ထို့ကြောင့် quartiles အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်း ဖြစ်ပါသည်။
![]()
ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် quartile ၏တန်ဖိုးမဟုတ်ဘဲ quartile ၏ အနေအထားကို ပြောပြသည်။ quartile သည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော အချက်အလက်ဖြစ်လိမ့်မည်။
သို့သော် တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ရလဒ်သည် ဒဿမ ဂဏန်း ဟုတ်၊ မဟုတ် ပေါ်မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-
- ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ quartile သည် အထက်ဖော်မြူလာမှ ပေးထားသည့် အနေအထားတွင်ရှိသော ဒေတာဖြစ်သည်။
- ဖော်မြူလာရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ quartile တန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-
![]()
x i နှင့် x i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။
ယခု၊ ထည့်သွင်းစဉ်းစားရမည့်အရာများစွာရှိသောကြောင့် quartiles တွက်ချက်ခြင်းသည် သင့်အတွက် အလွန်ရှုပ်ထွေးပေမည်။ ဒါပေမယ့် နောက်အပိုင်းမှာ နမူနာနှစ်ခုနဲ့၊ လက်တွေ့က ဘယ်လောက်ရိုးရှင်းလဲဆိုတာ သင်တွေ့ပါလိမ့်မယ်။
မှတ်ချက် – သိပ္ပံပညာအသိုင်းအဝိုင်းတွင်၊ quartiles များကို တွက်ချက်နည်းအပေါ် သဘောတူညီမှုမရှိသောကြောင့် အနည်းငယ်ကွဲပြားကြောင်း ရှင်းပြထားသည့် စာရင်းအင်းစာအုပ်ကို သင်ရှာတွေ့နိုင်ပါသည်။
Quartile များ တွက်ချက်ခြင်း နမူနာများ
Quartile များကို မည်ကဲ့သို့ တွက်ချက်သည်ကို အပြည့်အဝ နားလည်ရန်၊ အောက်ပါ ဖြေရှင်းနည်း နှစ်ခုကို တွေ့ရပါမည်။ ပထမတွင် quartiles များသည် integer များဖြစ်ပြီး ဒုတိယတွင် quartiles များသည် decimal number များဖြစ်သောကြောင့် မည်သည့် case နှစ်ခုကို တွေ့နိုင်သည်ကို သင်တွေ့နိုင်ပါသည်။
ဥပမာ ၁
- အောက်ပါဒေတာအတွဲ၏ လေးပုံသုံးပုံကို တွက်ချက်ပါ။

အထက်တွင်တွေ့မြင်ရသည့်အတိုင်း၊
![]()
ဤကိစ္စတွင် n သည် စုစုပေါင်းလေ့လာသုံးသပ်ချက်အရေအတွက် 15 ဖြစ်ပြီး၊ ထို့ကြောင့် ပထမ quartile ကိုရှာရန် n ကို 15 နှင့် k ဖြင့် 1 ဖြင့် အစားထိုးရပါမည်။
![]()
ထို့ကြောင့် ပထမအကြိမ် quartile သည် နံပါတ် 4 တွင် နံပါတ်များဖြစ်ပြီး ဤကိစ္စတွင် 39 ဖြစ်သည်။
အလားတူပင်၊ ကျွန်ုပ်တို့သည် coefficient k ကို 2 ဖြင့် အစားထိုးခြင်းဖြင့် ဒုတိယ quartile ကို တွက်ချက်သည်-
![]()
ထို့ကြောင့် Quartile 2 သည် တန်ဖိုး 48 နှင့် ကိုက်ညီသော အမျိုးအစားခွဲစာရင်းတွင် အဋ္ဌမမြောက်နံပါတ်ဖြစ်သည်။
နောက်ဆုံးတွင်၊ တတိယအကြိမ် quartile ကိုတွက်ချက်ရန် k =3 ဖြင့် နောက်ဆုံးအကြိမ် ဖော်မြူလာကို အသုံးပြုပါသည်။
![]()
Quartile 3 သည် ဒွါဒသမ အနေအထားတွင်ရှိသော အချက်အလက်နှင့် ကိုက်ညီသည်၊ ဆိုလိုသည်မှာ 60 ဖြစ်သည်။
ဥပမာ ၂
- အောက်ပါဒေတာစီးရီးများ၏ လေးပုံသုံးပုံကို ရှာပါ။

ဤဒုတိယဥပမာတွင်၊ ကျွန်ုပ်တို့တွင် ရှုမြင်မှု 24 ခုရှိသည်၊ ထို့ကြောင့် quartile ဖော်မြူလာမှရရှိသော ဂဏန်းများသည် ဒဿမဖြစ်သည်။
ကျွန်ုပ်တို့သည် ယေဘူယျဖော်မြူလာတွင် 1 အတွက် k ကို အစားထိုးခြင်းဖြင့် ပထမ quartile ၏ အနေအထားကို တွက်ချက်သည်-
![]()
![]()
သို့သော် ကျွန်ုပ်တို့သည် ဒဿမ နံပါတ် 6.25 ကိုရထားသည်၊ ထို့ကြောင့် ပထမ quartile သည် ဆဌမနှင့် သတ္တမဒေတာကြားတွင်ရှိပြီး 22 နှင့် 25 အသီးသီးရှိသည်။ ထို့ကြောင့်၊ တိကျသော quartile ကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရန် လိုအပ်ပါသည်။
![]()
ဤကိစ္စတွင် x i သည် 22၊ x i+1 25 ဖြစ်ပြီး d သည် ရရှိသော ဂဏန်းများ၏ ဒဿမအပိုင်းဖြစ်သည်၊ ဆိုလိုသည်မှာ 0.25 ဖြစ်သည်။ သို့တိုင်-
![]()
ယခု ကျွန်ုပ်တို့သည် ဒုတိယ quartile ကိုရှာဖွေရန် တူညီသောလုပ်ငန်းစဉ်ကို လုပ်ဆောင်သည်-
![]()
တစ်ဖန် ကျွန်ုပ်တို့သည် ဖော်မြူလာမှ ဒဿမဂဏန်းကို ရရှိသည်၊ ဤကိစ္စတွင်၊ ၎င်းသည် 12.5 ဖြစ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် 49 နှင့် 50 နှင့် သက်ဆိုင်သည့် ဒေတာဇယားရှိ ဆယ်နှစ်နှင့် ဆယ့်သုံးနံပါတ်များနှင့် တူညီသောဖော်မြူလာကို အသုံးပြုရမည်ဖြစ်သည်။
![]()
နောက်ဆုံးတွင်၊ တတိယ quartile ကိုရရှိရန် တူညီသောလုပ်ငန်းစဉ်ကို ထပ်လုပ်ပါသည်။
![]()
သို့သော် နံပါတ် 18.75 သည် နံပါတ် 18 နှင့် 19 ကြားဖြစ်သောကြောင့် တတိယ quartile သည် ဤရာထူးတန်ဖိုးများ (71 နှင့် 73) အကြားရှိမည်ဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ ၎င်းသည် အောက်ပါအသုံးအနှုန်းမှ ကျွန်ုပ်တို့ရရှိသောတန်ဖိုးဖြစ်သည်-
![]()
quartile ဂဏန်းတွက်စက်
quartiles များကိုတွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်သတ်မှတ်ထားသော ကိန်းဂဏန်းများကို ချိတ်ဆက်ပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။
အုပ်စုဖွဲ့ဒေတာတွင် လေးပုံတစ်ပုံ
ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့်အခါ quartile များကို တွက်ချက်ရန်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ quartile တွင် ကျနေသည့် ကြားကာလ သို့မဟုတ် bin ကို ဦးစွာရှာဖွေရန် လိုအပ်သည်-
![]()
ထို့ကြောင့် quartile သည် ယခင်ဖော်ပြချက်ဖြင့် ရရှိသော အကြိမ်အရေအတွက်ထက် အကြွင်းမဲ့ တိုးပွားနှုန်းသည် ချက်ချင်းကြီးနေသည့် ကြားကာလတွင် ဖြစ်လိမ့်မည်။
quartile ပိုင်သည့်ကြားကာလကို ကျွန်ုပ်တို့သိသည်နှင့်၊ quartile ၏အတိအကျတန်ဖိုးကိုရှာဖွေရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည်။
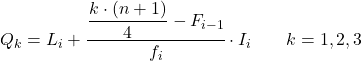
ရွှေ-
- L i သည် quartile တွင်ရှိသော ကြားကာလ၏ အနိမ့်ဆုံးကန့်သတ်ချက်ဖြစ်သည်။
- n သည် လေ့လာတွေ့ရှိချက် စုစုပေါင်း အရေအတွက်ဖြစ်သည်။
- F i-1 သည် ယခင်ကြားကာလ၏ ပကတိအကြိမ်အရေအတွက်ဖြစ်သည်။
- f i သည် quartile တည်ရှိနေသည့် ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
- I i သည် quartile interval ၏ width ဖြစ်သည်။
ဥပမာအနေဖြင့်၊ ဤနေရာတွင် အုပ်စုဖွဲ့ဒေတာအတွဲလိုက်တွင် quartiles တွက်ချက်ရန် လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။

ပထမ quartile ကို တွက်ချက်ရန်၊ ၎င်းတွင် ကျရောက်သည့် ကြားကာလကို ဦးစွာ ဆုံးဖြတ်ရပါမည်။ ဒါကိုလုပ်ဖို့၊ အောက်ပါပုံသေနည်းကို သုံးပါတယ်။
![]()
![]()
ထို့ကြောင့် ပထမအကြိမ် quartile သည် 7.75 ထက် ချက်ချင်းကြီးသော တိုးပွားလာသော အကြွင်းမဲ့ကြိမ်နှုန်းကြားကာလတွင် ဖြစ်လိမ့်မည်၊ ဤအခြေအနေတွင်၊ ၎င်းသည် ကြားကာလ [50.60) ဖြစ်ပြီး တိုးပွားလာသော absolute frequency သည် 15 ဖြစ်သည်။ ပြီးတော့ quartile ကြားကာလကို ကျွန်ုပ်တို့သိသည်နှင့်၊ ကျွန်ုပ်တို့သည် ဒုတိယလုပ်ငန်းစဉ်ဖော်မြူလာကို အသုံးပြုပါသည်။ :
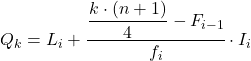
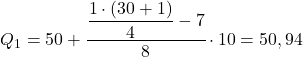
ဒုတိယ quartile ကိုရရှိရန် ကျွန်ုပ်တို့သည် အလားတူလုပ်ထုံးလုပ်နည်းကို ထပ်မံကျင့်သုံးပါသည်။ ကျွန်ုပ်တို့သည် quartile တည်ရှိသည့်ကြားကာလကို ဦးစွာဆုံးဖြတ်သည်-
![]()
15.5 ထက် များသော ကြိမ်နှုန်းချက်ချင်း ကြီးနေသော ကြားကာလသည် [60.70) ဖြင့် စုစည်းမှု ပကတိ အကြိမ်ရေ 26 ဖြစ်သည်။ ထို့ကြောင့် ဒုတိယ quartile မှာ-
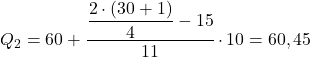
နောက်ဆုံးအနေနဲ့ တတိယ quartile ကိုရှာဖို့ လုပ်ငန်းစဉ်ကို ပြန်လုပ်ပါတယ်။ quartile ပါ၀င်သော ကြားကာလကို ဦးစွာ တွက်ချက်သည်-
![]()
23.25 အထက် ချက်ချင်း စုစည်းထားသော ပကတိကြိမ်နှုန်းသည် 26 ဖြစ်ပြီး၊ ထို့ကြောင့် တတိယမြောက် ကွာတားအပိုင်းသည် [60.70) ဖြစ်သည်။ ထို့ကြောင့် ဤကြားကာလဖြင့် quartile ကို တွက်ချက်ရန် ဖော်မြူလာကို အသုံးပြုပါသည်။
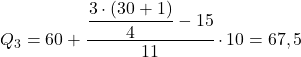
Quartiles တွေကို ဘာအတွက်အသုံးပြုကြသလဲ။
Quartiles များသည် အနေအထား၏အတိုင်းအတာတစ်ခုဖြစ်သော ကြောင့် ၎င်းတို့ကို data မည်ကဲ့သို့နေရာချထားသည်ကိုသိရန်အသုံးပြုသည်။ တစ်နည်းဆိုရသော်၊ quartile သုံးခု၏တန်ဖိုးများသည် နမူနာရှိ ကျပန်းဒေတာပစ္စည်းတစ်ခုသည် အလွန်ကြီးမားခြင်း၊ အလွန်သေးငယ်ခြင်း သို့မဟုတ် ပျမ်းမျှတန်ဖိုးဖြစ်ခြင်းရှိ၊ မရှိ သိရှိနိုင်စေပါသည်။
အကယ်၍ ကျွန်ုပ်တို့သည် နမူနာမှ ဒေတာတစ်ပိုင်းကို ကျပန်းယူပါက၊ ၎င်းကို quartiles များနှင့် နှိုင်းယှဉ်ခြင်းဖြင့် ၎င်း၏တန်ဖိုးသည် မြင့်မားခြင်း သို့မဟုတ် နိမ့်ခြင်းရှိ၊ မရှိ သိရှိနိုင်ပါသည်။ ကျပန်းဒေတာတန်ဖိုးသည် ပထမ quartile ထက်နည်းပါက၊ ၎င်းသည် သေးငယ်သောတန်ဖိုးဖြစ်မည်ဖြစ်သော်လည်း ၎င်း၏တန်ဖိုးသည် တတိယ quartile ထက်ကြီးပါက၊ ၎င်းသည် ကြီးမားသောတန်ဖိုးဖြစ်လိမ့်မည်။ အလားတူပင်၊ ထိုဒေတာ၏တန်ဖိုးသည် ပထမနှင့်တတိယ quartile အကြားဖြစ်ပါက၊ ၎င်းသည် အလယ်အလတ်တန်ဖိုးဖြစ်သည်။
အခြားတစ်ဖက်တွင်၊ quartile များကို interquartile range (သို့မဟုတ် interquartile range) ကဲ့သို့သော အခြားသော ကိန်းဂဏန်းဆိုင်ရာတိုင်းတာမှုများကို တွက်ချက်ရန်နှင့် box နှင့် whisker plot (သို့မဟုတ် boxplot) ကဲ့သို့သော ပုံများပြုလုပ်ရန်အတွက်လည်း အသုံးပြုပါသည်။