Stata တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်နည်း။
variable နှစ်ခုသည် linear ဆက်ဆံရေးတစ်ခုရှိသောအခါ၊ ၎င်းတို့၏ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် ရိုးရှင်းသော linear regression ကို မကြာခဏအသုံးပြုနိုင်သည် ။

သို့သော်၊ ကိန်းရှင်နှစ်ခုသည် လေးထောင့်ပုံစံ ဆက်နွယ်မှုရှိပါက၊ ၎င်းတို့၏ ဆက်ဆံရေးကို တွက်ချက်ရန် လေးထောင့်ဆုတ်ယုတ်မှုကို သင်သုံးနိုင်သည်။

ဤသင်ခန်းစာသည် Stata တွင် လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။
ဥပမာ- Stata ရှိ လေးပုံတပုံ ဆုတ်ယုတ်မှု
အလုပ်လုပ်တဲ့နာရီအရေအတွက်နဲ့ ပျော်ရွှင်မှုကြားက ဆက်နွယ်မှုကို နားလည်ချင်တယ်ဆိုပါစို့။ ကျွန်ုပ်တို့တွင် တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်နှင့် ပတ်သက်သည့် အောက်ပါဒေတာနှင့် လူ 16 ဦးအတွက် ပျော်ရွှင်မှုအဆင့် (0 မှ 100 အထိ) အစီရင်ခံတင်ပြသည်-
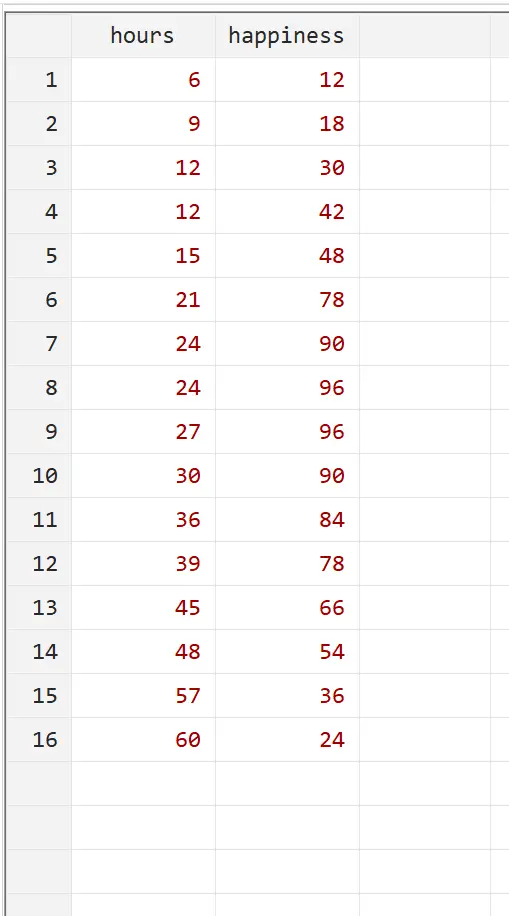
ထိပ်တန်းမီနူးရှိ Data > Data Editor > Data Editor (တည်းဖြတ်) ကို အသုံးပြု၍ ဤဒေတာအတိအကျကို Stata ထဲသို့ ထည့်သွင်းခြင်းဖြင့် သင်သည် ဤဥပမာကို ပြန်လည်ထုတ်လုပ်နိုင်ပါသည်။
Stata တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။
အဆင့် 1- ဒေတာကို မြင်ယောင်ကြည့်ပါ။
quadratic regression ကိုအသုံးမပြုမီ၊ ရှင်းပြထားသော variable (နာရီ) နှင့် response variable (happiness) တို့သည် quadratic အမှန်ဖြစ်ကြောင်း သေချာစေရမည်။ ထို့ကြောင့် Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် scatterplot ကို အသုံးပြု၍ ဒေတာကို မြင်ယောင်ကြည့်ကြပါစို့ ။
ပျော်ရွှင်မှု နာရီတွေကို ခွဲထုတ်လိုက်ပါ။
၎င်းသည် အောက်ဖော်ပြပါ ဖြန့်ကျက်ကွက်ကို ထုတ်ပေးသည်-
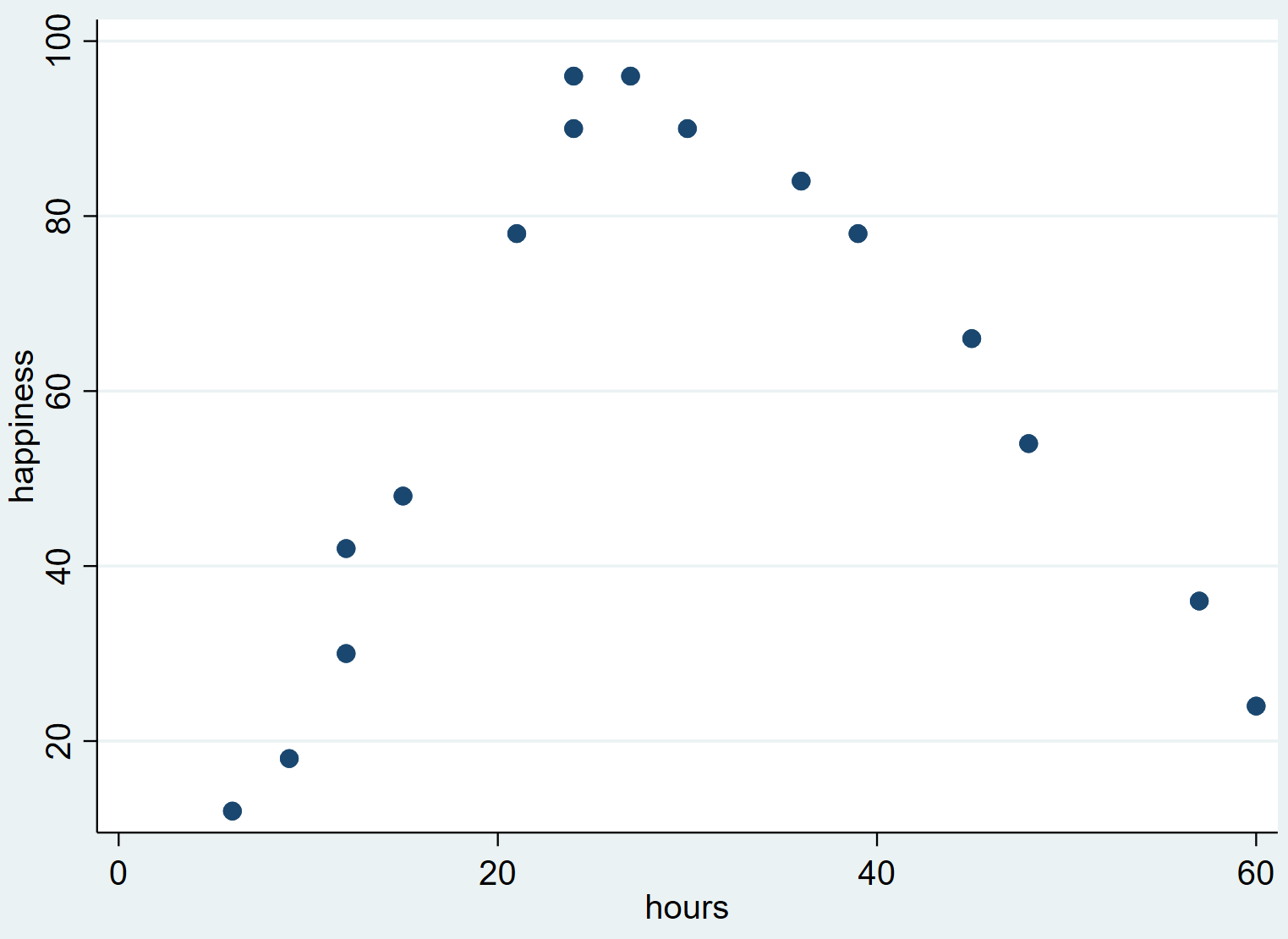
အလုပ်ချိန် အရေအတွက် သုညမှ တစ်နေရာသို့ တိုးလာသည်နှင့်အမျှ ပျော်ရွှင်မှု တိုးလာတတ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သော်လည်း အလုပ်ချိန် 30 ဝန်းကျင်ထက် ကျော်လွန်လာသည်နှင့်အမျှ ကျဆင်းလာပါသည်။
scatterplot တွင် ပြောင်းပြန်ထားသော ဤ “ U” ပုံသဏ္ဍာန်သည် အလုပ်ချိန်နှင့် ပျော်ရွှင်မှုကြားတွင် လေးပုံတစ်ပုံ ဆက်စပ်မှုရှိကြောင်း ညွှန်ပြသည်၊ ဆိုလိုသည်မှာ ဤဆက်ဆံရေးကို တွက်ချက်ရန် လေးထောင့်ပုံသဏ္ဍာန်ကို သုံးသင့်သည်။
အဆင့် 2- လေးထောင့်ပုံစံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါ။
Quadratic regression model ကို data နဲ့ အံမဝင်ခင်မှာ၊ ကျွန်ုပ်တို့ရဲ့ နာရီ ခန့်မှန်းကိန်းရှင်ရဲ့ နှစ်ထပ်ကိန်းတန်ဖိုးတွေအတွက် variable အသစ်တစ်ခုကို ဖန်တီးဖို့လိုအပ်ပါတယ်။ Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် ၎င်းကို လုပ်ဆောင်နိုင်သည် ။
gen hours2 = နာရီ*နာရီ
ထိပ်တန်းမီနူးမှ Data > Data Editor > Data Editor (Browse) သို့သွားခြင်းဖြင့် ဤကိန်းရှင်အသစ်ကို ကြည့်ရှုနိုင်ပါသည်။
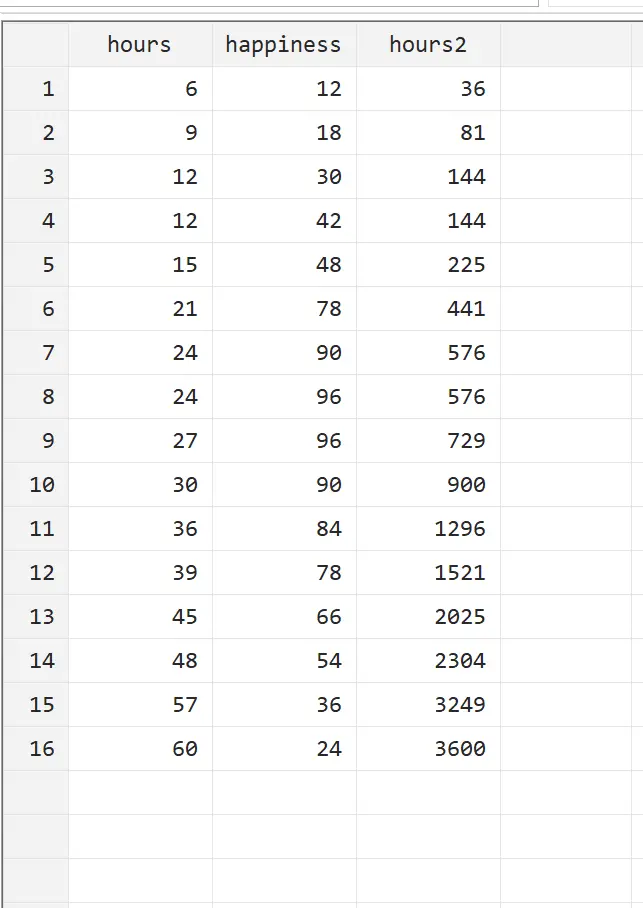
နာရီ 2 သည် ရိုးရိုးနာရီ နှစ်ထပ်ဖြစ်သည်ကို ကျွန်ုပ်တို့မြင်နိုင်သည်။ ယခု ကျွန်ုပ်တို့သည် နာရီ နှင့် နာရီ 2 ကို တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ရှင်းလင်းချက်နှင့် ပျော်ရွှင်မှု အဖြစ် နာရီနှင့် နာရီ 2 ကို အသုံးပြု၍ လေးထောင့်ကိန်းဂဏန်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်နိုင်ပါပြီ။ လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန်၊ Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ပါ။
ပျော်ရွှင်မှု နာရီများ နောက်ပြန်ဆုတ်ခြင်း ၂
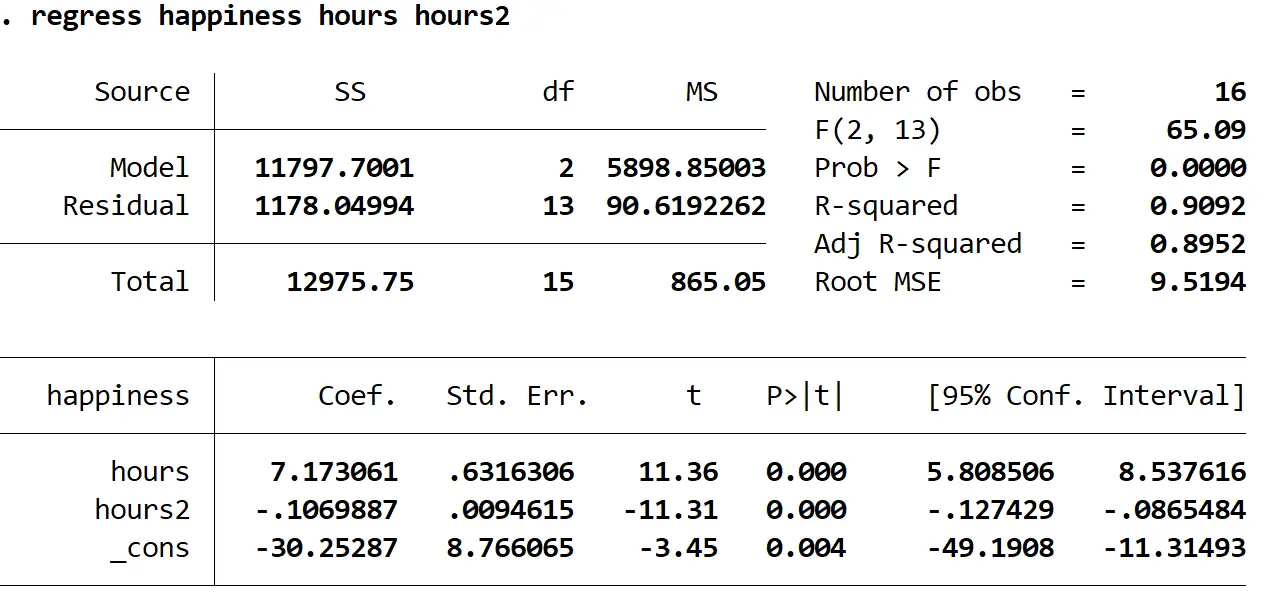
ရလဒ်တွင် စိတ်ဝင်စားစရာအကောင်းဆုံးဂဏန်းများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည်။
Prob > F: 0,000။ ၎င်းသည် အလုံးစုံဆုတ်ယုတ်မှုအတွက် p-တန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ဆိုလိုသည်မှာ ခန့်မှန်းသူကိန်းရှင်များသည် နာရီ နှင့် နာရီ 2 ပေါင်းစပ်ထားသော တုံ့ပြန်မှုမပြောင်းလဲနိုင်သော ပျော်ရွှင်မှု နှင့် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်ဆံရေးရှိသည်။
R နှစ်ထပ်ကိန်း- 0.9092။ ဤသည်မှာ explanatory variable ဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ ပျော်ရွှင်မှုကွဲပြားမှု၏ 90.92% ကို နာရီ နှင့် နာရီ 2 ဖြင့် ရှင်းပြနိုင်သည်။
Regression equation: output table တွင်ပြသထားသော coefficient တန်ဖိုးများကို အသုံးပြု၍ regression equation ကို ဖန်တီးနိုင်သည်။ ဤကိစ္စတွင်၊ ညီမျှခြင်းမှာ-
ခန့်မှန်းထားသော ပျော်ရွှင်မှု = -30.25287 + 7.173061 (နာရီ) – 0.1069887 ( 2 နာရီ)
တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်ဖြင့် လူတစ်ဦးချင်းစီ၏ ခန့်မှန်းထားသော ပျော်ရွှင်မှုကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။
ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် နာရီ 60 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 14.97 ရှိသင့်သည်-
ခန့်မှန်းထားသော ပျော်ရွှင်မှု = -30.25287 + 7.173061(60) – .1069887(60 2 ) = 14.97 .
အပြန်အလှန်အားဖြင့် တစ်ပတ်လျှင် နာရီ 30 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 88.65 ရှိသင့်သည်-
ခန့်မှန်းထားသော ပျော်ရွှင်မှု = -30.25287 + 7.173061(30) – .1069887(30 2 ) = 88.65 .
အဆင့် 3- ရလဒ်များကို သတင်းပို့ပါ။
နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ လေးပုံတပုံ ဆုတ်ယုတ်မှု၏ ရလဒ်များကို အစီရင်ခံလိုပါသည်။ ဤသည်မှာ မည်သို့လုပ်ဆောင်ရမည်ကို ဥပမာတစ်ခုဖြစ်သည်။
လူတစ်ဦးချင်းစီမှ အလုပ်လုပ်သော နာရီအရေအတွက်နှင့် ၎င်းတို့၏ သက်ဆိုင်ရာ ပျော်ရွှင်မှုအဆင့် (0 မှ 100) အကြား ဆက်နွယ်မှုကို တွက်ချက်ရန် လေးလေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုတစ်ခုကို လုပ်ဆောင်ခဲ့သည်။ ခွဲခြမ်းစိတ်ဖြာမှုတွင် လူ ၁၆ ဦး၏ နမူနာကို အသုံးပြုခဲ့သည်။
ရလဒ်များသည် ရှင်းလင်းချက်ပြကွက်များ နာရီ နှင့် နာရီ 2 နှင့် တုံ့ပြန်မှုပြောင်းလဲနိုင်သော ပျော်ရွှင်မှု (F(2, 13) = 65.09၊ p < 0.0001) အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်ဆံရေးရှိကြောင်း ပြသခဲ့သည်။
ဤရှင်းပြချက်နှစ်ခုသည် ပျော်ရွှင်မှုတွင် ရှင်းပြထားသော ကွဲပြားမှု၏ 90.92% ကို ပေါင်းစပ်ထားသည်။
ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-
ခန့်မှန်းထားသော ပျော်ရွှင်မှု = -30.25287 + 7.173061 (နာရီ) – 0.1069887 ( 2 နာရီ)