သစ်ပင်ပုံကားချပ်

အားဖြင့် Benjamin Anderson ဩဂုတ် 4, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် သစ်ပင်ပုံကားချပ်ဟူသည် အဘယ်နည်းနှင့် ပြုလုပ်ပုံတို့ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ သစ်ပင်တည်ဆောက်ပုံနမူနာများ၊ ဤပုံကြမ်းအမျိုးအစား၏ အားသာချက်များနှင့် ထို့အပြင် တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကို သင်တွေ့လိမ့်မည်။

သစ်ပင်ဆိုတာဘာလဲ။

ဖြစ်နိုင်ခြေသစ်ပင် ဟုလည်း ခေါ်သော သစ်ပင်ပုံဇယား သည် စမ်းသပ်မှုတစ်ခု၏ ဖြစ်နိုင်ခြေရှိသော ရလဒ်အားလုံးကို ၎င်းတို့၏ဖြစ်နိုင်ခြေများနှင့်အတူ ဂရပ်ဖစ်သရုပ်ဖော်ခြင်းဖြစ်သည်။

ထို့ကြောင့်၊ နမူနာနေရာတစ်ခုတွင် ဖြစ်နိုင်ချေရှိသောရလဒ်အားလုံးကို ဂရပ်ဖစ်နှင့် ၎င်းတို့၏ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် သစ်ပင်ပုံကားချပ်ကို အသုံးပြုသည်။

ရလဒ် ( node ) တစ်ခုစီကို နောက်ဆုံးရလဒ်များ မရောက်မချင်း ဖြစ်နိုင်သည့်ရလဒ်အသစ်များ ( အကိုင်းအခက်များ ) အဖြစ်သို့ အကိုင်းအခက်တစ်ခုစီကို သစ်ပင်ပုံပုံစံဖြင့် ပြုလုပ်ထားသည်။

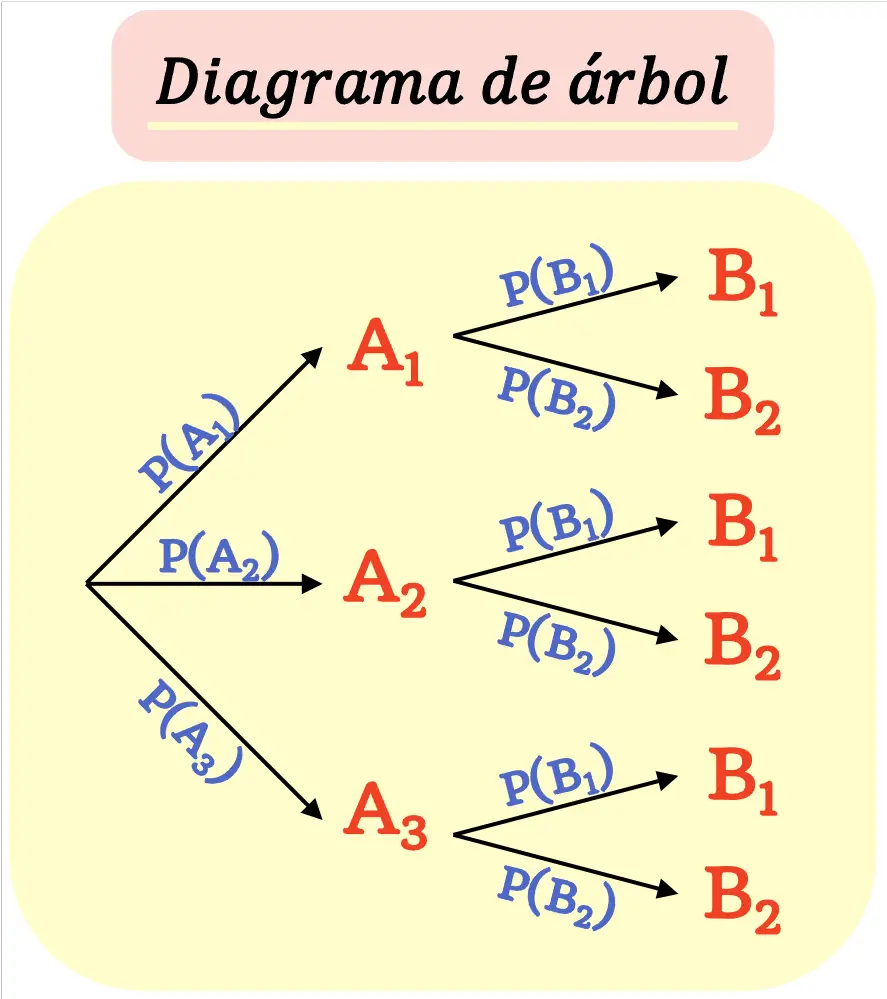
node တစ်ခုမှထွက်လာသောအကိုင်းအခက်အားလုံး၏ဖြစ်နိုင်ခြေပေါင်းလဒ်သည် 1 နှင့် ညီမျှရမည်ကို မှတ်သားထားသင့်သည်။

သစ်ပင်ပုံဆွဲနည်း

သစ်ပင်တစ်ပင်ဖန်တီး ရန် အောက်ပါအဆင့်များအတိုင်း လုပ်ဆောင်ရပါမည်။

သစ်ပင်ပုံတစ်ပုံကို ဖန်တီးရာတွင် ပထမအဆင့်မှာ ဖြစ်နိုင်သည့်ရလဒ်တစ်ခုစီအတွက် အကိုင်းအခက်တစ်ခုဆွဲရန်ဖြစ်သည်။ ယင်းတို့သည် ပထမမျိုးဆက် အကိုင်းအခက်များ ဖြစ်လိမ့်မည်။
ထို့နောက်၊ အစီအစဉ်တစ်ခုစီနှင့်ဆက်စပ်နိုင်ခြေကို ၎င်း၏သက်ဆိုင်ရာဌာနခွဲသို့ ပေါင်းထည့်သည်။
ပထမမျိုးဆက်ဌာနခွဲတစ်ခုစီ၏ အဆုံးသည် နောက်ဆက်တွဲဖြစ်နိုင်သောဖြစ်ရပ်များ၏ အကိုင်းအခက်များကို ကိုယ်စားပြုရမည့် ဆုံမှတ်တစ်ခုဖြစ်သည်။
ပထမအကိုင်းအခက်များတွင်ကဲ့သို့၊ ကျွန်ုပ်တို့သည် ကိုယ်စားပြုဖြစ်ရပ်များ၏ ဖြစ်နိုင်ခြေများကို ထည့်ရပါမည်။
အဆင့် 3 နှင့် 4 ကို သင်နောက်ဆုံးဆုံမှတ်များရောက်ရှိသည်အထိ၊ ဆိုလိုသည်မှာ စမ်းသပ်မှု၏ဖြစ်နိုင်ချေအဆုံးသတ်များအထိ ထပ်လုပ်ပါ။

အဆင့်တစ်ခုရှိ ဘဏ်ခွဲအရေအတွက်သည် မတူညီသောအဆင့်ရှိ ဘဏ်ခွဲအရေအတွက်နှင့် တူညီရန်မလိုအပ်ကြောင်း သတိပြုပါ။ အလားတူပင် ဖြစ်နိုင်ချေရလဒ်တစ်ခုမှ ထွက်ပေါ်လာသော ဘဏ်ခွဲအရေအတွက်သည် တူညီသောအဆင့်တွင်ပင် ကွဲပြားနိုင်သည်။

သစ်ပင်ဥပမာ

ယခု ကျွန်ုပ်တို့သည် သစ်ပင်ပုံကားချပ်တစ်ခု ဖန်တီးခြင်း၏ အဓိပ္ပါယ်နှင့် သီအိုရီကို သိရှိပြီး သဘောတရားကို ပိုမိုနားလည်ရန် လက်တွေ့ကမ္ဘာဥပမာကို တစ်ဆင့်ပြီးတစ်ဆင့် ကြည့်ကြပါစို့။

လွတ်လပ်သောဒင်္ဂါးသုံးပြားကို အကြွေစေ့ပစ်ခြင်း၏ ဖြစ်နိုင်ခြေသစ်ပင်ကို တည်ဆောက်ပါ။ ထို့နောက် သုံးကြိမ်စလုံးတွင် ဦးခေါင်းရရှိရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

စာရေးတဲ့အခါ ဖြစ်နိုင်တဲ့ ရလဒ် နှစ်ခုပဲ ရှိတယ်၊ ခေါင်း ဒါမှမဟုတ် အမြီးတွေ ရနိုင်တယ်။ ထို့ကြောင့်၊ အကြွေစေ့ကိုပစ်သောအခါ ဦးခေါင်း သို့မဟုတ် အမြီးများရနိုင်ခြေမှာ-

$P(\text{cara})=\cfrac{1}{2}=0,5$

$P(\text{cruz})=\cfrac{1}{2}=0,5$

ဖြစ်နိုင်ချေရလဒ်များ၏ ဖြစ်နိုင်ခြေများကို ကျွန်ုပ်တို့သိသည်နှင့်၊ ကျွန်ုပ်တို့သည် သစ်ပင်ပုံဇယားကို ကိုယ်စားပြုရန် ဆက်လက်လုပ်ဆောင်ပါသည်။

အကြွေစေ့ပစ်ခြင်းများသည် သီးခြားဖြစ်သောကြောင့်၊ ခေါင်း သို့မဟုတ် အမြီးများရယူခြင်း၏ ဖြစ်နိုင်ခြေသည် တစ်ကြိမ်စီတိုင်းအတွက် အမြဲတူညီနေမည်ဖြစ်သည်။ ထို့ကြောင့် သစ်ပင်ကိုတည်ဆောက်ရန်အတွက် အကိုင်းအခက်နှစ်ခု (ဦးခေါင်းနှင့်အမြီးများ) ပြုလုပ်ထားသော ပစ်တိုင်းအတွက် တူညီသောဖြစ်နိုင်ခြေကို ကိုယ်စားပြုရပါမည်။

သစ်ပင်ကို ဖန်ဆင်းပြီးသည်နှင့် ကျွန်ုပ်တို့လုပ်ရမည့်အရာမှာ အကြွေစေ့သုံးပြားကို လွှင့်ပစ်ခြင်း၏ ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ခြင်းဖြစ်သည်။

သစ်ပင်ပုံတစ်ပုံ၏ ဖြစ်နိုင်ခြေရလဒ်ကို တွက်ချက်ရန်၊ ကပ်လျက်အကိုင်းအခက်အားလုံး၏ ဖြစ်နိုင်ခြေများကို မြှောက်ရပါမည်။

ထို့ကြောင့်၊ ဤအခြေအနေတွင် ကျွန်ုပ်တို့သည် လိုချင်သောရလဒ်သို့ပို့ဆောင်သည့်လမ်းကြောင်း၏ဖြစ်နိုင်ခြေများဖြစ်သောကြောင့် ဦးခေါင်းရရှိရန်ဖြစ်နိုင်ခြေအားလုံးကို မြှောက်ထားရပါမည်။

ထို့ကြောင့်၊ အကြွေစေ့သုံးကြိမ်တွင် ဦးခေါင်းရရှိရန် ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

$P(\text{cara-cara-cara})=0,5\cdot 0,5\cdot 0,5=0,125$

အတိုချုပ်အားဖြင့်၊ ဆက်တိုက် ခေါင်းသုံးကြိမ်ရနိုင်ခြေသည် 12.5% ဖြစ်သည်။

ကြွပ်ကြွပ်အိတ်လေ့ကျင့်ခန်း

ရွာတစ်ရွာတွင် ခရေကန် ၃ ခုသာ ရှိသည်- ကလေး ၆၀% သည် ခရက်ချ် A သို့ သွားကြသည်၊ ကရိန် B မှ ၃၀% နှင့် ကရိန် C တွင် ၁၀%၊ ထို့အပြင် ကရားသုံးခုတွင် လူ ၅၅% မှာ မိန်းကလေးများဖြစ်သည်။ သစ်ပင်ကိုတည်ဆောက်ပြီး အောက်ပါဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။

ကလေးတစ်ဦးကို ကျပန်းရွေးချယ်လိုက်သောအခါ ၎င်းမှာ နေ့ထိန်း B မှ မိန်းကလေးဖြစ်နိုင်ချေရှိသည်။
ကလေးတစ်ဦးသည် နေ့ထိန်းဂေဟာတစ်ခုခုမှ ကျပန်းရွေးချယ်ခံရသည့်အခါ ယောက်ျားလေးဖြစ်နိုင်ခြေရှိသည်။

ဖြေရှင်းချက်ကိုကြည့်ပါ။

နေ့ထိန်းကျောင်းအားလုံးရှိ မိန်းကလေးများ၏ အချိုးအစားသည် 55% ဖြစ်ပါက 1 အနှုတ် 0.55 ကို နုတ်ရုံဖြင့် ယောက်ျားလေးရာခိုင်နှုန်းကို တွက်ချက်သည်-

$P(\text{chico})=1-0,55=0,45$

ဖြစ်နိုင်ခြေအားလုံးကို ယခုကျွန်ုပ်တို့သိပြီးဖြစ်နိုင်ခြေသစ်ပင်ကို ဖြစ်နိုင်ချေအားလုံးကို ဖန်တီးနိုင်သည်-

ထို့ကြောင့် နေ့ထိန်း B မှ မိန်းကလေးတစ်ဦးကို ကျပန်းရွေးချယ်ခြင်း၏ ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

$P(\text{chica guarder\'ia B})=0,30\cdot 0,55=\bm{0,165}$

အခြားတစ်ဖက်တွင်၊ မည်သည့် နေ့ထိန်းကျောင်းတွင်မဆို ယောက်ျားလေးတစ်ဦးကို ရွေးချယ်ရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန်၊ နေ့ထိန်းကျောင်းတစ်ခုစီအတွက် ယောက်ျားလေးတစ်ဦးကို ရွေးချယ်ခြင်း၏ ဖြစ်နိုင်ခြေကို ဦးစွာရှာဖွေပြီး ၎င်းတို့ကို ပေါင်းထည့်ရမည်-

$P(\text{chico guarder\'ia A})=0,6\cdot 0,45=0,27$

$P(\text{chico guarder\'ia B})=0,30\cdot 0,45=0,135$

$P(\text{chico guarder\'ia C})=0,10\cdot 0,45=0,045$

$P(\text{chico guarder\'ia A, B o C})=0,27+0,135+0,045=\bm{0,45}$

သစ်ပင်ဖွဲ့စည်းပုံ၏အားသာချက်များ

သစ်ပင်ဖွဲ့စည်းပုံသွင်ပြင်လက္ခဏာများကြောင့်၊ ဤစာရင်းအင်းဂရပ်အမျိုးအစား၏ အားသာချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

သစ်ပင်ပုံများသည် ဆုံးဖြတ်ချက်များချရာတွင် အလွန်အသုံးဝင်သည်။
ဖြစ်နိုင်ချေရှိသော ရလဒ်များကြားရှိ ဆက်စပ်မှုကို ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုနိုင်သည်။
ပြဿနာတစ်ခုရဲ့ မူလဇစ်မြစ်ကို ရှာရတာ အရမ်းအဆင်ပြေတယ်။
ဖြစ်နိုင်ခြေနှင့် စာရင်းဇယားပြဿနာများကို ဖြေရှင်းရန် ပိုမိုလွယ်ကူစေသည်။
သစ်ပင်ပုံကားချပ်သည် အတွေးအမြင်များကို စုစည်းစေပြီး အခြေအနေကို ခွဲခြမ်းစိတ်ဖြာရန် ကူညီပေးသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။