သရုပ်ဖော်ခြင်း သို့မဟုတ် အကြမ်းဖျင်းစာရင်းဇယား- ကွာခြားချက်ကား အဘယ်နည်း။

စာရင်းအင်းနယ်ပယ်တွင် အဓိကအကိုင်းအခက်နှစ်ခုရှိသည်။

• ဖော်ပြချက်စာရင်းဇယား
• ကိန်းဂဏန်းစာရင်းဇယား

ဤကျူတိုရီရယ်တွင် အကိုင်းအခက်နှစ်ခုကြား ခြားနားချက်တစ်ခုစီသည် အချို့သောအခြေအနေများတွင် အဘယ်ကြောင့်အသုံးဝင်ကြောင်း ရှင်းပြထားသည်။

ဖော်ပြချက် စာရင်းဇယား

အတိုချုပ်အားဖြင့်၊ ဖော်ပြချက်စာရင်းဇယားများသည် အကျဉ်းချုပ်စာရင်းဇယားများ၊ ဂရပ်များနှင့် ဇယားများကို အသုံးပြု၍ ဒေတာကုန်ကြမ်း အစုအဝေးကို ဖော်ပြရန် ရည်ရွယ်သည်။

ကိန်းဂဏန်းစာရင်းဇယားများသည် သင့်အား ဒေတာတန်ဖိုးများ၏ အတန်းများနှင့် ဒေတာတန်ဖိုးများကို အတန်းလိုက်ကြည့်ရုံထက် ပိုမိုလျင်မြန်လွယ်ကူစွာ နားလည်နိုင်စေသောကြောင့် ၎င်းတို့သည် အသုံးဝင်ပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် သီးခြားကျောင်းတစ်ကျောင်းတွင် ကျောင်းသား 1,000 ၏ စာမေးပွဲရမှတ်များကို ပြသသည့် ဒေတာအကြမ်းအစုံရှိသည် ဆိုကြပါစို့။ ကျွန်ုပ်တို့သည် ပျမ်းမျှ စာမေးပွဲရမှတ်အပြင် စာမေးပွဲရမှတ်များ ဖြန့်ဝေမှုကို စိတ်ဝင်စားပေမည်။

သရုပ်ဖော်ကိန်းဂဏန်းများကို အသုံးပြု၍ ပျမ်းမျှရမှတ်ကို ရှာဖွေနိုင်ပြီး ရမှတ်များခွဲဝေမှုကို မြင်သာစေရန် ကူညီပေးသည့် ဂရပ်တစ်ခုကို ဖန်တီးနိုင်သည်။

ဒါက ဒေတာအကြမ်းကို ကြည့်ရုံထက် ကျောင်းသားစာမေးပွဲရမှတ်တွေကို နားလည်နိုင်စေတယ်။

သရုပ်ဖော်ကိန်းဂဏန်းများ၏ ဘုံပုံစံများ

ဖော်ပြချက်စာရင်းဇယား၏ ယေဘူယျပုံစံသုံးမျိုးရှိသည်။

1. စာရင်းဇယားအကျဉ်းချုပ်။ ၎င်းတို့သည် ကိန်းဂဏန်းတစ်ခုတည်းကို အသုံးပြု၍ ဒေတာကို အကျဉ်းချုပ်ဖော်ပြသည့် ကိန်းဂဏန်းများဖြစ်သည်။ အနှစ်ချုပ်စာရင်းဇယား၏ ယေဘူယျ အမျိုးအစား နှစ်မျိုးရှိသည်။

• ဗဟိုသဘောထားကို အတိုင်းအတာများ : ဤကိန်းဂဏာန်းများသည် ဒေတာအစုတစ်ခု၏ ဗဟိုတည်နေရာကို ဖော်ပြသည်။ ဥပမာများတွင် ပျမ်းမျှ   နှင့် ပျမ်းမျှ ။
• Dispersion အစီအမံများ- ဤနံပါတ်များသည် ဒေတာအစုံရှိ တန်ဖိုးများ ဖြန့်ဖြူးမှုကို ဖော်ပြသည်။ ဥပမာများတွင် ကြားကာလ ၊ interquartile အကွာအဝေး ၊ စံသွေဖည်မှု နှင့် ကွဲလွဲမှုတို့ ပါဝင်သည်။

2. ဂရပ်ဖစ်များ ဇယားကွက်များသည် ဒေတာကို မြင်ယောင်နိုင်ရန် ကူညီပေးသည်။ ဒေတာကို မြင်ယောင်ရန် အသုံးပြုလေ့ရှိသော ဇယားအမျိုးအစားများတွင် အကွက်ကွက်များ ၊ ဟီစတိုဂရမ်များ ၊ ပင်စည်နှင့် အရွက်ကွက်များ၊ နှင့် ဖြန့်ကြဲကွက်များ ပါဝင်သည်။

3. စားပွဲများ ဇယားများသည် ဒေတာဖြန့်ဝေပုံကို နားလည်ရန် ကူညီပေးနိုင်သည်။ အသုံးများသော ဇယားအမျိုးအစားမှာ အချို့သော အပိုင်းအခြားများအတွင်း ဒေတာတန်ဖိုး မည်မျှကျဆင်းသည်ကို ပြောပြသည့် ကြိမ်နှုန်းဇယား ဖြစ်သည်။

သရုပ်ဖော်ကိန်းဂဏန်းများကို အသုံးပြုခြင်း ဥပမာ

အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့ကမ္ဘာတွင် သရုပ်ဖော်ကိန်းဂဏန်းများကို မည်ကဲ့သို့ အသုံးပြုနိုင်ကြောင်း ဖော်ပြသည်။

ကျောင်းတစ်ကျောင်းတွင် ကျောင်းသား ၁၀၀၀ စလုံး တူညီသော စာမေးပွဲကို ဖြေဆိုကြသည်ဟု ယူဆသည်။ ကျွန်ုပ်တို့သည် စမ်းသပ်မှုရလဒ်များ ဖြန့်ဝေခြင်းကို နားလည်လိုသောကြောင့် အောက်ပါဖော်ပြချက်စာရင်းအင်းများကို အသုံးပြုပါသည်။

1. စာရင်းဇယားအကျဉ်းချုပ်

ပျမ်းမျှ- 82.13 ။ ကျောင်းသား 1,000 တွင် ပျမ်းမျှ စာမေးပွဲရမှတ်သည် 82.13 ရှိသည်ဟု ကျွန်ုပ်တို့ကို ပြောပြသည်။

အလယ်အလတ်- 84။ ကျောင်းသားအားလုံး၏ ထက်ဝက်သည် 84 အထက် ရမှတ်ဖြစ်ပြီး ကျန်တစ်ဝက်မှာ 84 အောက်တွင် ရကြောင်း ကျွန်ုပ်တို့ကို ပြောပြသည်။

အများဆုံး- 100။ အနည်းဆုံး- 45။ မည်သည့်ကျောင်းသားမှ ရရှိသော အများဆုံးရမှတ်မှာ 100 ဖြစ်ပြီး အနိမ့်ဆုံးရမှတ်မှာ 45 ဖြစ်သည်။ အများဆုံးနှင့် အနိမ့်ဆုံးအကြား ကွာခြားချက်ကို ပြောပြသည့် အပိုင်းအခြား သည် 55 ဖြစ်သည်။

2. ဂရပ်ဖစ်

စမ်းသပ်မှုရလဒ်များ ဖြန့်ဝေမှုကို မြင်သာစေရန်၊ ကျွန်ုပ်တို့သည် ကြိမ်နှုန်းများကိုကိုယ်စားပြုရန် စတုဂံဘားများကိုအသုံးပြုသည့် ဇယားအမျိုးအစားဖြစ်သည့် histogram ကို ဖန်တီးနိုင်ပါသည်။

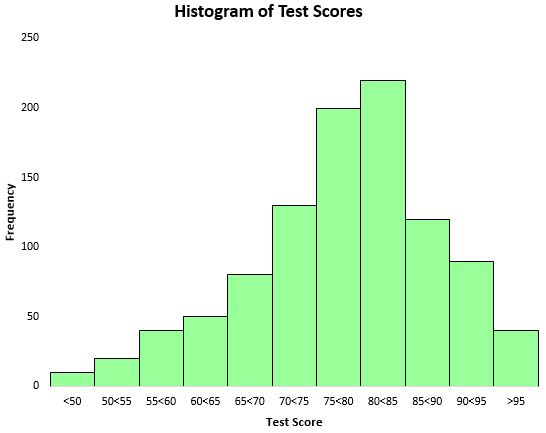
ဤဟစ်စတိုဂရမ်ကို အခြေခံ၍ စာမေးပွဲရမှတ်များ ဖြန့်ဝေမှုသည် အကြမ်းဖျင်းအားဖြင့် ခေါင်းလောင်းပုံသဏ္ဍာန်ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။ ကျောင်းသားအများစုသည် ရမှတ် 70 နှင့် 90 အကြားရကြပြီး 95 အထက်ရမှတ် အလွန်နည်းပြီး 50 အောက်ရမှတ်များပင် နည်းပါးသည်။

3. စားပွဲများ

ရမှတ်များခွဲဝေမှုကို နားလည်ရန် နောက်ထပ်လွယ်ကူသောနည်းလမ်းမှာ ကြိမ်နှုန်းဇယားတစ်ခုဖန်တီးရန်ဖြစ်သည်။ ဥပမာအားဖြင့်၊ အောက်ဖော်ပြပါ ကြိမ်နှုန်းဇယားသည် မတူညီသော ဘောင်များကြားတွင် ရမှတ်ရရှိသော ကျောင်းသားများ၏ ရာခိုင်နှုန်းကို ပြသည်-

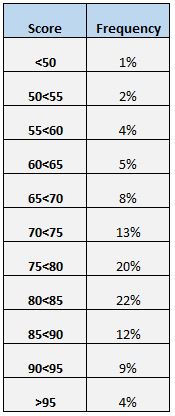
95 အထက် ရမှတ် စုစုပေါင်း ကျောင်းသားများ၏ 4% သာ တွေ့နိုင်သည်။ (12% + 9% + 4% = ) ကျောင်းသားအားလုံး၏ 25% သည် 85 နှင့် အထက် ရမှတ်များဖြစ်သည် ။

ဒေတာတန်ဖိုးများ၏ ရာခိုင်နှုန်းတစ်ခုအထက် သို့မဟုတ် အောက်တွင် ရှိနေသည်ကို သိရှိလိုပါက ကြိမ်နှုန်းဇယားသည် အထူးအသုံးဝင်ပါသည်။ ဥပမာအားဖြင့်၊ ကျောင်းက လက်ခံနိုင်သော စာမေးပွဲရမှတ်ကို 75 အထက် ရမှတ်ဟု သတ်မှတ်သည်ဆိုပါစို့။

ကြိမ်နှုန်းဇယားကိုကြည့်လိုက်ရင် (20% + 22% + 12% + 9% + 4% = ) ကျောင်းသားတွေရဲ့ 67% ဟာ စာမေးပွဲမှာ လက်ခံနိုင်လောက်တဲ့ရမှတ်ကို ရရှိခဲ့ပါတယ်။

ကိန်းဂဏန်းစာရင်းဇယား

အတိုချုပ်အားဖြင့်၊ ကောက်ချက်ချသောစာရင်းအင်းများသည် နမူနာထုတ်ယူသည့် ပိုကြီးသောလူဦးရေနှင့်ပတ်သက်၍ ကောက်ချက် ဆွဲရန် သေးငယ်သောဒေတာနမူနာကို အသုံးပြုသည်။

ဥပမာအားဖြင့်၊ နိုင်ငံတစ်ခုရှိ လူသန်းပေါင်းများစွာ၏ နိုင်ငံရေး ဦးစားပေးမှုများကို ကျွန်ုပ်တို့ နားလည်လိုပေမည်။

သို့သော် နိုင်ငံအတွင်းရှိ လူတစ်ဦးစီတိုင်းကို စစ်တမ်းကောက်ယူရန် အချိန်ကုန်ပြီး စျေးကြီးသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် အမေရိကန်လူမျိုး ၁,၀၀၀ ကို သေးငယ်သော စစ်တမ်းတစ်ခုယူ၍ လူဦးရေတစ်ခုလုံးနှင့်ပတ်သက်သော ကောက်ချက်ဆွဲရန် စစ်တမ်းရလဒ်များကို အသုံးပြုမည်ဖြစ်သည်။

ဤသည်မှာ အကြမ်းဖျင်းစာရင်းဇယား၏ အနှစ်သာရတစ်ခုလုံးဖြစ်သည်- လူဦးရေနှင့်ပတ်သက်သောမေးခွန်းတစ်ခုကို ကျွန်ုပ်တို့ဖြေလိုသည်၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ထိုလူဦးရေ၏နမူနာငယ်အတွက် ဒေတာကိုရယူပြီး လူဦးရေနှင့်ပတ်သက်သော ကောက်ချက်ဆွဲရန်အတွက် နမူနာဒေတာကို အသုံးပြုပါသည်။

ကိုယ်စားလှယ်တစ်ဦး၏အရေးပါမှုနမူနာ

လူဦးရေဆိုင်ရာနမူနာကို ကောက်ချက်ဆွဲရန် ကျွန်ုပ်တို့၏စွမ်းဆောင်နိုင်မှုကို ယုံကြည်မှုရှိစေရန်အတွက်၊ ကျွန်ုပ်တို့တွင် ကိုယ်စားလှယ်နမူနာ တစ်ခုရှိရမည်၊ ဆိုလိုသည်မှာ လူဦးရေရှိလူတစ်ဦးချင်းစီ၏ ဝိသေသလက္ခဏာများ နမူနာနမူနာသည် နမူနာနှင့် နီးကပ်စွာကိုက်ညီမှုရှိစေရမည်၊ လက္ခဏာများ။ စုစုပေါင်းလူဦးရေ။

အကောင်းဆုံးကတော့၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏နမူနာကို ကျွန်ုပ်တို့လူဦးရေ၏ “မီနီဗားရှင်း” နှင့် ဆင်တူစေလိုပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် 50% မိန်းကလေးများနှင့် 50% ယောက်ျားလေးများပါ၀င်သော ကျောင်းသားဦးရေကို ကောက်ချက်ချလိုပါက၊ ကျွန်ုပ်တို့နမူနာတွင် ယောက်ျားလေး 90% နှင့် 10% မိန်းကလေးများသာ ပါဝင်ပါက ကျွန်ုပ်တို့၏နမူနာတွင် ကိုယ်စားပြုမည်မဟုတ်ပါ။

ကျွန်ုပ်တို့၏နမူနာသည် စုစုပေါင်းလူဦးရေနှင့် ဆင်တူခြင်းမရှိပါက၊ နမူနာမှ ရလဒ်များကို အလုံးစုံလူဦးရေသို့ စိတ်ချယုံကြည်စွာ ယေဘူယျဖော်ပြနိုင်မည်မဟုတ်ပေ။

ကိုယ်စားလှယ်နမူနာရယူနည်း

ကိုယ်စားလှယ်နမူနာရရှိရန် အခွင့်အလမ်းကို အမြင့်ဆုံးရရန်၊ သင်သည် အရာနှစ်ခုကို အာရုံစိုက်သင့်သည်-

1. ကျပန်းနမူနာနည်းလမ်းကို သင်အသုံးပြုကြောင်း သေချာပါစေ။

ကိုယ်စားပြုနမူနာကို ထုတ်လုပ်နိုင်ဖွယ်ရှိသည့် သင်အသုံးပြုနိုင်သော ကျပန်း နမူနာနည်းလမ်း များစွာ ရှိပြီး၊ အပါအဝင်၊

• ရိုးရှင်းသောကျပန်းနမူနာ
• စနစ်တကျ ကျပန်းနမူနာ
• အစုလိုက် ကျပန်းနမူနာ
• အချိုးကျ ကျပန်းနမူနာ

ကျပန်းနမူနာနည်းလမ်းများသည် လူဦးရေ၏အဖွဲ့ဝင်တစ်ဦးစီတွင် နမူနာတွင်ပါဝင်ရန် တူညီသောအခွင့်အရေးရှိသောကြောင့် ကိုယ်စားလှယ်နမူနာများကို ထုတ်ပေးလေ့ရှိပါသည်။

2. သင်၏နမူနာအရွယ်အစားသည် အလုံအလောက်ကြီးကြောင်း သေချာပါစေ ။

သင့်လျော်သောနမူနာနည်းလမ်းကို အသုံးပြုခြင်းအပြင်၊ နမူနာသည် ပိုမိုကြီးမားသောလူဦးရေကို ယေဘုယျဖော်ပြနိုင်စေရန် ဒေတာလုံလောက်မှုရှိစေရန်အတွက် နမူနာသည် ကြီးမားကြောင်းသေချာရန် အရေးကြီးပါသည်။

သင်၏နမူနာအရွယ်အစားကို ဆုံးဖြတ်ရန်၊ သင်လေ့လာနေသော လူဦးရေ၏ အရွယ်အစား၊ သင်အသုံးပြုလိုသော ယုံကြည်မှုအဆင့်နှင့် သင်လက်ခံနိုင်ဖွယ်ရှိသည့် အမှား၏အနားသတ်တို့ကို ထည့်သွင်းစဉ်းစားရန် လိုအပ်သည်။

ကံကောင်းထောက်မစွာ၊ သင်သည် ဤတန်ဖိုးများကို ရိုက်ထည့်ရန် အွန်လိုင်းဂဏန်းတွက်စက်များကို အသုံးပြုနိုင်ပြီး သင်၏နမူနာအရွယ်အစားသည် မည်သည့်အရာဖြစ်သင့်သည်ကို ကြည့်ရှုနိုင်ပါသည်။

ယေဘုယျ ကိန်းဂဏန်းစာရင်းဇယားပုံစံများ

ကိန်းဂဏန်းစာရင်းဇယား၏ ယေဘူယျပုံစံသုံးမျိုးရှိသည်။

1. ယူဆချက် စမ်းသပ်ခြင်း။

ကျွန်ုပ်တို့သည် လူဦးရေနှင့်ပတ်သက်သော မေးခွန်းများကို မကြာခဏဖြေကြားလိုပါသည်-

• အိုဟိုင်းယိုးပြည်နယ်တွင် ကိုယ်စားလှယ်လောင်းတစ်ဦးကို ထောက်ခံသည့် ရာခိုင်နှုန်းသည် ၅၀ ရာခိုင်နှုန်းထက် ပိုများနေပါသလား။
• အပင်တစ်ပင်၏ ပျမ်းမျှအမြင့်သည် ၁၄ လက်မနှင့် ညီမျှပါသလား။
• ကျောင်း A နှင့် ကျောင်း B တွင် ကျောင်းသားများ၏ ပျမ်းမျှအမြင့် ကွာခြားမှုရှိပါသလား။

ဤမေးခွန်းများကို ဖြေဆိုရန်၊ လူဦးရေနှင့်ပတ်သက်သော ကောက်ချက်ဆွဲရန် နမူနာတစ်ခုမှ ဒေတာကို အသုံးပြုခွင့်ပေးသည့် သီအိုရီစစ်ဆေးမှုကို လုပ်ဆောင်နိုင်ပါသည်။

2. ယုံကြည်မှုကြားကာလများ ။

တစ်ခါတစ်ရံ ကျွန်ုပ်တို့သည် လူဦးရေအတွက် တိကျသောတန်ဖိုးကို ခန့်မှန်းလိုပါသည်။ ဥပမာအားဖြင့်၊ သြစတြေးလျရှိ အပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်ကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပေမည်။

နိုင်ငံတွင်းရှိ အပင်တိုင်းကို လှည့်ပတ်တိုင်းတာမည့်အစား အပင်၏နမူနာအနည်းငယ်ကို ကောက်ယူပြီး တစ်ခုစီတိုင်းထွာနိုင်ပါသည်။ ထို့နောက် လူဦးရေ၏ ပျမ်းမျှအမြင့်ကို ခန့်မှန်းရန် နမူနာရှိ အပင်များ၏ ပျမ်းမျှအမြင့်ကို အသုံးပြုနိုင်သည်။

သို့သော်လည်း ကျွန်ုပ်တို့၏နမူနာသည် ပြီးပြည့်စုံသော လူဦးရေခန့်မှန်းချက်ကို မပေးနိုင်ပါ။ ကံကောင်းထောက်မစွာ၊ လူဦးရေအစစ်အမှန် ကန့်သတ်ဘောင်သည် ကျွန်ုပ်တို့ယုံကြည်စိတ်ချရသော တန်ဖိုးများစွာကို ပေးဆောင်သည့် ယုံကြည်မှုကြားကာလ တစ်ခုကို ဖန်တီးခြင်းဖြင့် ကျွန်ုပ်တို့သည် ဤမသေချာမရေရာမှုများကို တွက်ချက်နိုင်ပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် [၁၃.၂၊ ၁၄.၈] ၏ 95% ယုံကြည်မှုကြားကာလကို ထုတ်လုပ်နိုင်သည်၊ ဆိုလိုသည်မှာ ဤအပင်မျိုးစိတ်များ၏ စစ်မှန်သော ပျမ်းမျှအမြင့်မှာ 13.2 လက်မနှင့် 14.8 လက်မကြားရှိ 95% သေချာပါသည်။

၃။ ဆုတ်ယုတ်မှု ။

တစ်ခါတစ်ရံ လူဦးရေတစ်ခုရှိ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ကျွန်ုပ်တို့ နားလည်လိုကြသည်။

ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် စာသင်ချိန်နာရီများသည် စာမေးပွဲရမှတ်များ နှင့် ဆက်စပ်မှုရှိမရှိ သိလိုသည်ဆိုကြပါစို့။ ဤမေးခွန်းကိုဖြေဆိုရန်၊ ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်ခြင်းခွဲခြမ်းစိတ်ဖြာခြင်း ဟုခေါ်သော နည်းပညာတစ်ခုကို လုပ်ဆောင်နိုင်သည် ။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် လေ့လာခဲ့သည့် နာရီအရေအတွက်နှင့် ကျောင်းသား 100 အတွက် စာမေးပွဲရမှတ်များကို ကြည့်ရှုနိုင်ပြီး ကိန်းရှင်နှစ်ခုကြားတွင် သိသာထင်ရှားသော ဆက်နွယ်မှုရှိမရှိ သိရှိနိုင်ရန် ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုကို လုပ်ဆောင်နိုင်ပါသည်။

ဆုတ်ယုတ်မှု၏ p-တန်ဖိုးကို သိသာထင်ရှားစွာ တွေ့ရှိပါက ၊ ကျောင်းသားဦးရေတွင် ဤကိန်းရှင်နှစ်ခုကြားတွင် သိသာထင်ရှားသော ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည်။

သရုပ်ဖော်ပုံနှင့် နိယာမကိန်းဂဏန်းများကြား ခြားနားချက်

အနှစ်ချုပ်အားဖြင့်၊ သရုပ်ဖော်ခြင်းနှင့် နိယာမကိန်းဂဏန်းများကြား ခြားနားချက်ကို အောက်ပါအတိုင်း ဖော်ပြနိုင်ပါသည်။

သရုပ်ဖော်စာရင်းအင်းများသည် အချက်အလက်အစုအဝေးကို ဖော်ပြရန် အကျဉ်းချုပ်စာရင်းဇယားများ၊ ဂရပ်များနှင့် ဇယားများကို အသုံးပြုသည်။

ဒေတာတန်ဖိုးအားလုံးကို မဖြတ်သန်းဘဲ ဒေတာအစုတစ်ခုကို လျင်မြန်လွယ်ကူစွာ နားလည်နိုင်ရန် ဤအရာက အသုံးဝင်ပါသည်။

အကြမ်းဖျင်းစာရင်းအင်းများသည် ပိုများသောလူဦးရေများအကြောင်း ကောက်ချက် ဆွဲရန် နမူနာများကို အသုံးပြုသည်။

လူဦးရေနှင့်ပတ်သက်၍ သင်ဖြေလိုသောမေးခွန်းအပေါ် မူတည်၍ အောက်ပါနည်းလမ်းများထဲမှ တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော နည်းလမ်းများကို အသုံးပြုရန် သင်ဆုံးဖြတ်နိုင်သည်- သီအိုရီစစ်ဆေးမှု၊ ယုံကြည်မှုကြားကာလများနှင့် ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှု။

ဤနည်းလမ်းများထဲမှ တစ်ခုကို အသုံးပြုရန် ရွေးချယ်ပါက၊ သင့်နမူနာသည် သင့်လူဦးရေ၏ ကိုယ်စားပြုဖြစ်ရမည် ၊ မဟုတ်ပါက သင်ဆွဲသော ကောက်ချက်များသည် ယုံကြည်စိတ်ချရမည်မဟုတ်ကြောင်း သတိရပါ။