သိပ်သည်းမှု လုပ်ဆောင်ချက်

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် density function သည် အဘယ်နည်း၊ ဖြစ်နိုင်ခြေတစ်ခုအား density function မှ တွက်ချက်ပုံနှင့် ဤ probabilistic function ၏ ဝိသေသလက္ခဏာများကို ရှာဖွေတွေ့ရှိမည်ဖြစ်ပါသည်။ ထို့အပြင်၊ density function နှင့် distribution function အကြား ကွာခြားချက်များကို သင်တွေ့မြင်နိုင်မည်ဖြစ်ပါသည်။

သိပ်သည်းဆလုပ်ဆောင်ချက်ကဘာလဲ။

density function သည် probability density function ဟုခေါ်သည် ၊ သည် စဉ်ဆက်မပြတ် ကျပန်းကိန်းရှင်သည် သတ်မှတ်ထားသော တန်ဖိုးတစ်ခုပေါ်တွင် ဆက်တိုက်လုပ်ဆောင်သော ဖြစ်နိုင်ခြေကို ဖော်ပြသည့် သင်္ချာလုပ်ဆောင်ချက်တစ်ခုဖြစ်သည်။

တစ်နည်းဆိုရသော်၊ ကိန်းရှင်တစ်ခုနှင့်ဆက်စပ်နေသော သိပ်သည်းဆလုပ်ဆောင်ချက်သည် ကိန်းရှင်တန်ဖိုးတစ်ခုယူသည့်ဖြစ်နိုင်ခြေများကို သင်္ချာနည်းအားဖြင့် သတ်မှတ်ပေးသည်။

ဥပမာအားဖြင့်၊ လူဦးရေတွင် အရွယ်ရောက်ပြီးသူသည် 1.80 မီတာထက် မြင့်သောဖြစ်နိုင်ခြေသည် 35% ဖြစ်သည်၊ ထို့နောက် density function သည် ထိုဖြစ်နိုင်ခြေကို တွက်ချက်သောအခါ ဖြစ်နိုင်ခြေ 35% ကို ညွှန်ပြလိမ့်မည်ဆိုပါစို့။

တစ်ခါတစ်ရံတွင် ဖြစ်နိုင်ခြေသိပ်သည်းမှုလုပ်ဆောင်ချက်ကို PDF အဖြစ် အတိုချုံးခေါ်သည်။

သိပ်သည်းဆ လုပ်ဆောင်မှုဖြင့် ဖြစ်နိုင်ခြေကို တွက်ချက်ပါ။

စဉ်ဆက်မပြတ်ကိန်းရှင်သည် ကြားကာလတစ်ခုအတွင်း တန်ဖိုးတစ်ခုယူဆောင်သွားသည့်ဖြစ်နိုင်ခြေကို ရှာဖွေရန်၊ ကြားကာလ၏ကန့်သတ်ချက်များကြားရှိ ကိန်းရှင်နှင့်ဆက်စပ်နေသော သိပ်သည်းဆလုပ်ဆောင်မှု၏ ပေါင်းစပ်မှုကို တွက်ချက်ရန် လိုအပ်သည်။

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

ရွှေ

$f(x)$

စဉ်ဆက်မပြတ် random variable ၏ density function ဖြစ်သည်။

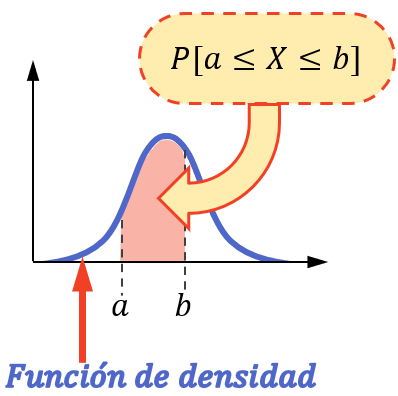
သို့မဟုတ် တစ်နည်းအားဖြင့်၊ ကြားကာလတစ်ခုအတွင်း တန်ဖိုးတစ်ခုယူသည့် variable ၏ဖြစ်နိုင်ခြေသည် ထိုကြားကာလရှိ သိပ်သည်းမှုလုပ်ဆောင်မှုအောက်ရှိ ဧရိယာနှင့် ညီမျှသည်။

ကိန်းဂဏန်းကိန်းရှင်သည် ပုံမှန်ဖြန့်ဖြူးမှု၊ ထပ်ကိန်းခွဲဝေမှု၊ Poisson ဖြန့်ဝေမှုစသည်ဖြင့် ဆက်တိုက်ဖြန့်ဝေမှုနောက်တွင်သာ ဖြစ်နိုင်ခြေ တွက်ချက်မှုကို ဤနည်းဖြင့် လုပ်ဆောင်နိုင်ကြောင်း သတိပြုပါ။

density function ၏ ဂုဏ်သတ္တိများ

သိပ်သည်းဆ လုပ်ဆောင်မှုတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

density function ၏တန်ဖိုးသည် x ၏တန်ဖိုးတိုင်းအတွက် သုည သို့မဟုတ် အပေါင်းဖြစ်သည်။

$f(x)\geq 0$

ထို့အပြင် density function ၏ အမြင့်ဆုံးတန်ဖိုးသည် 1 နှင့် ညီမျှသည်။

$f(x)\leq 1$

တကယ်တော့၊ density function graph အောက်ရှိ စုစုပေါင်းဧရိယာသည် ဖြစ်နိုင်ခြေအားလုံး၏ set နှင့် သက်ဆိုင်သောကြောင့် variable မည်သို့ပင်ဖြစ်စေ 1 နှင့် အမြဲတမ်းညီမျှပါသည်။

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

ယခင်အပိုင်းတွင် ရှင်းပြထားသည့်အတိုင်း၊ ကြားကာလတစ်ခုအတွင်း စဉ်ဆက်မပြတ်ကိန်းရှင်တစ်ခုသည် တန်ဖိုးတစ်ခုယူဆောင်သွားနိုင်သည့်ဖြစ်နိုင်ခြေကို ထိုကြားကာလရှိ သိပ်သည်းဆလုပ်ဆောင်မှု၏ ပေါင်းစည်းမှုနှင့် တွက်ချက်သည်။

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

သိပ်သည်းမှု လုပ်ဆောင်ချက်နှင့် ဖြန့်ဖြူးမှု လုပ်ဆောင်ချက်

ဤနောက်ဆုံးအပိုင်းတွင်၊ ၎င်းတို့သည် ယေဘူယျအားဖြင့် ရှုပ်ထွေးနေသော ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်နှစ်မျိုးဖြစ်သောကြောင့် သိပ်သည်းမှုလုပ်ဆောင်ချက်နှင့် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက် ကွာခြားပုံကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

သင်္ချာနည်းအားဖြင့်၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်သည် သိပ်သည်းဆလုပ်ဆောင်မှု၏ ပေါင်းစည်းမှုနှင့် ညီမျှသည် ၊ ထို့ကြောင့် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်သည် စဉ်ဆက်မပြတ်ကိန်းရှင်တစ်ခု၏ စုစည်းဖြစ်နိုင်ခြေကို ဖော်ပြသည်။

ဆိုလိုသည်မှာ၊ မည်သည့်တန်ဖိုးအတွက်မဆို ဖြန့်ဝေမှုလုပ်ဆောင်ချက်၏ ပုံသည် ကိန်းရှင်သည် ထိုတန်ဖိုး သို့မဟုတ် နိမ့်သောတန်ဖိုးကို ယူသည့်ဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။

ထို့ကြောင့် ဤ function အမျိုးအစားနှစ်ခုကြားရှိ သင်္ချာဆိုင်ရာ ဆက်နွယ်မှုသည် အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

ရွှေ

$f(x)$

density function နှင့်

$F(x)$

ဖြန့်ဖြူးရေးလုပ်ဆောင်ချက်ဖြစ်သည်။

ပုံမှန်ဖြန့်ဝေမှု၏ပျမ်းမျှ 1 နှင့် 0.5 ၏စံသွေဖည်မှုနောက်ဆက်တွဲဖြစ်သော ကိန်းရှင်တစ်ခု၏ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် ဆက်စပ်နေသော သိပ်သည်းဆလုပ်ဆောင်မှု၏ ဂရပ်ဖစ်ဖော်ပြချက်သည် မည်သို့ပြောင်းလဲသည်ကို သတိပြုပါ။

ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုအကြား ကွာခြားချက်

ဖြန့်ဖြူးမှုအင်္ဂါရပ်အကြောင်း ပိုမိုလေ့လာရန်၊ အောက်ပါလင့်ခ်ကို နှိပ်ပါ။

➤ ဖြန့ ်ဖြူးမှုလုပ်ဆောင်ချက်ကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။