သီးသန့် ယူနီဖောင်း ဖြန့်ဖြူးခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် သီးခြားယူနီဖောင်းဖြန့်ဖြူးခြင်းမှာ အဘယ်အရာနှင့် ၎င်း၏ ဝိသေသဖော်မြူလာဖြစ်သည်ကို ရှင်းပြထားသည်။ အလားတူ၊ သီးခြားယူနီဖောင်းဖြန့်ဖြူးခြင်း၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုကို သင်မြင်နိုင်မည်ဖြစ်ပြီး ၎င်း၏ဂုဏ်သတ္တိများကား အဘယ်နည်း။

ခွဲဝေယူနီဖောင်း ဖြန့်ဝေခြင်းဆိုသည်မှာ အဘယ်နည်း။

Discrete uniform distribution သည် discrete probability distribution တစ်ခုဖြစ်ပြီး တန်ဖိုးများအားလုံးသည် ညီမျှခြင်းဖြစ်နိုင်သည်၊ ဆိုလိုသည်မှာ discrete uniform distribution တစ်ခုတွင်၊ တန်ဖိုးများအားလုံးသည် တူညီသောဖြစ်နိုင်ခြေရှိသည် ။

ဥပမာအားဖြင့်၊ ဖြစ်နိုင်ခြေရလဒ်များအားလုံး (1၊ 2၊ 3၊ 4၊ 5၊ သို့မဟုတ် 6) သည် တူညီသောဖြစ်နိုင်ခြေရှိသောကြောင့် အသေတစ်ခု၏အလိပ်ကို သီးခြားတူညီသောဖြန့်ဝေမှုဖြင့် သတ်မှတ်နိုင်သည်။

ယေဘူယျအားဖြင့်၊ သီးခြားယူနီဖောင်း ဖြန့်ဖြူးမှုတွင် ဖြန့်ဖြူးမှုယူနိုင်သည့် ဖြစ်နိုင်ချေတန်ဖိုးများ အကွာအဝေးကို သတ်မှတ်ပေးသော a နှင့် b တို့၏ လက္ခဏာရပ်ဘောင်နှစ်ခုရှိသည်။ ထို့ကြောင့်၊ variable တစ်ခုကို discrete uniform distribution ဖြင့် သတ်မှတ်သောအခါ၊ ၎င်းကို Uniform(a,b) ဟု ရေးထားသည်။

ရလဒ်အားလုံးသည် တူညီသောဖြစ်နိုင်ခြေရှိလျှင် ၎င်းသည် စမ်းသပ်ချက်သည် ကျပန်းဖြစ်သည်ဟု ဆိုလိုသောကြောင့် သီးခြားတူညီဝတ်စုံဖြန့်ဝေမှုကို ကျပန်းစမ်းသပ်မှုများကို ဖော်ပြရန်အတွက် အသုံးပြုနိုင်သည်။

သီးခြားယူနီဖောင်း ဖြန့်ဖြူးရေးဖော်မြူလာ

ယခု ကျွန်ုပ်တို့သည် သီးခြားယူနီဖောင်း ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို သိသောအခါ၊ ဤအမျိုးအစား ဖြန့်ဖြူးမှု၏ တန်ဖိုးများ၏ အသွင်အပြင်၏ ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် ဖော်မြူလာက မည်သည်ကို တွေ့ရမည်ဖြစ်ပါသည်။

သီးခြားယူနီဖောင်းဖြန့်ဖြူးမှု၏ ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်သည် စဉ်ဆက်မပြတ်ဖြစ်ပြီး ၎င်း၏တန်ဖိုးသည် ဖြစ်နိုင်ချေရလဒ်များ၏ စုစုပေါင်းအရေအတွက်ထက် တစ်ခုနှင့်ညီမျှသည်။ ထို့ကြောင့် discrete uniform distribution အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်း ဖြစ်ပါသည်။

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

အခြားတစ်ဖက်တွင်၊ discrete uniform distribution ၏ စုစည်းဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

ရွှေ

$a$

နှင့်

$b$

discrete uniform distribution ၏ ဝိသေသ ဘောင်များဖြစ်သည်။

သီးခြားယူနီဖောင်း ဖြန့်ချီမှု ပုံကြမ်း

သီးခြားယူနီဖောင်း ဖြန့်ဖြူးမှုသည် ကြားကာလတစ်ခုအတွင်း အချို့သောတန်ဖိုးများကိုသာ ယူနိုင်သောကြောင့် ၎င်း၏ဂရပ်ဖစ်ဖော်ပြမှုတွင် အမှတ်များ ပါဝင်သည်။ ထို့အပြင်၊ ဖြစ်နိုင်ခြေအားလုံးသည် တန်းတူဖြစ်သည်၊ ထို့ကြောင့် discrete uniform distribution ရှိ အမှတ်များအားလုံးသည် တူညီသောဒေါင်လိုက်နိတ်များရှိသည်။

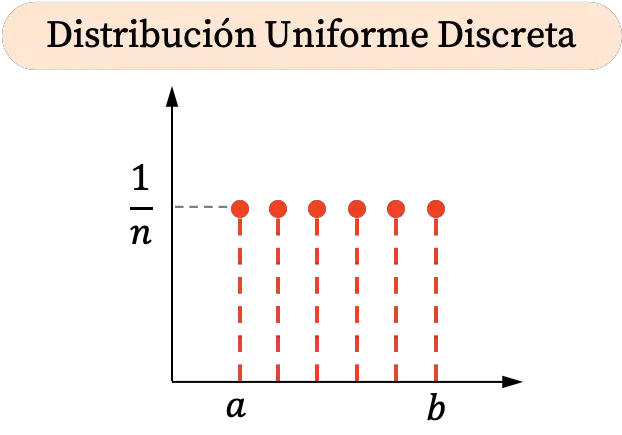
အခြားတစ်ဖက်တွင်၊ discrete uniform distribution ၏ စုစည်းဖြစ်နိုင်ခြေဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်-

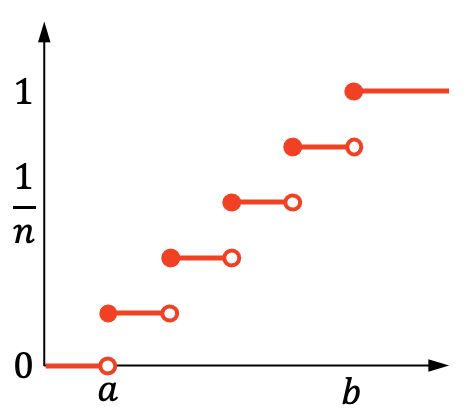
သီးခြားယူနီဖောင်း ဖြန့်ဖြူးမှု၏ တိုးပွားနိုင်ခြေ

ခွဲဝေယူနီဖောင်း၏ လက္ခဏာများ

သီးခြားယူနီဖောင်း ဖြန့်ဖြူးမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။

သီးခြားတူညီသော ဖြန့်ဖြူးမှုကို ခွဲဝေမှု၏ ဖြစ်နိုင်ချေတန်ဖိုးများ အကွာအဝေးကို ဆုံးဖြတ်ပေးသော ကိန်းပြည့် ဘောင်နှစ်ခုဖြစ်သည့် a နှင့် b တို့က သတ်မှတ်သည်။

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

သီးခြားယူနီဖောင်းခွဲဝေမှု၏ပျမ်းမျှသည် ၎င်း၏ဝိသေသကန့်သတ်ဘောင်နှစ်ခု၏ပေါင်းလဒ်နှင့် ညီမျှသည်။

$E[X]=\cfrac{a+b}{2}$

သီးခြားယူနီဖောင်းခွဲဝေမှု၏ ပျမ်းမျှသည် ၎င်း၏ဆိုလိုရင်းနှင့် ညီမျှသောကြောင့် ၎င်းကို တူညီသောအသုံးအနှုန်းဖြင့် တွက်ချက်သည်-

$Me=\cfrac{a+b}{2}$

သီးခြားယူနီဖောင်းခွဲဝေမှု၏ကွဲလွဲမှုသည် စုစုပေါင်းရလဒ်အရေအတွက်၏ နှစ်ထပ်ကိန်းနှင့် ညီမျှသည်။

$Var(X)=\cfrac{n^2-1}{12}$

သီးခြားယူနီဖောင်းဖြန့်ဖြူးမှုသည် ၎င်း၏ဆိုလိုရင်းနှင့်ပတ်သက်၍ အချိုးညီညီဖြစ်သောကြောင့်၊ ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှု၏ လွဲချော်မှုကိန်းဂဏန်းမှာ သုညဖြစ်သည်။

$A=0$

ခွဲခြမ်းစိတ်ဖြာခြင်း၏ kurtosis ကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်နိုင်ပါသည်။

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

တူညီဝတ်စုံဖြန့်ဖြူးခြင်းနှင့် စဉ်ဆက်မပြတ် တူညီဝတ်စုံဖြန့်ဖြူးခြင်း။

နောက်ဆုံးတွင်၊ ၎င်းတို့သည် အလားတူဖြစ်နိုင်ခြေ ဖြန့်ဝေမှု အမျိုးအစား နှစ်ခုဖြစ်ကြသော်လည်း သိသိသာသာ ကွာခြားမှု ရှိသောကြောင့် နောက်ဆုံးတွင်၊ သီးခြား ယူနီဖောင်း ဖြန့်ဖြူးခြင်းနှင့် စဉ်ဆက်မပြတ် ယူနီဖောင်း ဖြန့်ဖြူးခြင်း အကြား ခြားနားချက်ကို ကျွန်ုပ်တို့ မြင်ရပါမည်။

သီးခြားယူနီဖောင်း ဖြန့်ဖြူးခြင်းနှင့် စဉ်ဆက်မပြတ် ယူနီဖောင်း ဖြန့်ဖြူးခြင်းကြား ခြားနားချက် သည် ၎င်းတို့၏ ဖြစ်နိုင်ချေတန်ဖိုးများတွင် ရှိသည်။ သီးခြားယူနီဖောင်းဖြန့်ဖြူးမှုသည် ကြားကာလတစ်ခုအတွင်း အချို့သောတန်ဖိုးများကိုသာ ယူနိုင်သော်လည်း စဉ်ဆက်မပြတ်ယူနီဖောင်းဖြန့်ဖြူးမှုသည် ၎င်းသတ်မှတ်ထားသည့်ကြားကာလတွင် မည်သည့်တန်ဖိုးကိုမဆို ယူနိုင်သည်။

ယေဘုယျအားဖြင့်၊ သီးခြားတူညီသော ဖြန့်ဝေမှုများသည် ကိန်းပြည့်တန်ဖိုးများကိုသာ ယူနိုင်သော်လည်း စဉ်ဆက်မပြတ် ယူနီဖောင်းဖြန့်ဝေမှုများသည် ဒဿမတန်ဖိုးများကို ယူနိုင်သည်။

➤- စဉ်ဆက်မပြတ် ယူနီဖောင်း ဖြန့်ဖြူးမှုကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။