အချိုးအစား ကွဲပြားမှုကို နမူနာယူခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် အချိုးအစားနမူနာဖြန့်ဝေမှုတွင် ကွာခြားချက်နှင့် ကိန်းဂဏန်းစာရင်းအင်းများတွင် အသုံးပြုသည့်အရာတို့ကို ရှင်းပြထားသည်။ အချိုးအစားနမူနာဖြန့်ချီရေးဖော်မြူလာနှင့် အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်း ကွာခြားချက်ကိုလည်း တင်ပြထားပါသည်။

အချိုးအစားကွာခြားချက်၏နမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။

အချိုးအစားနမူနာဖြန့်ဝေမှုတွင် ကွာခြားချက် မှာ မတူညီသောလူဦးရေနှစ်ခုမှ ဖြစ်နိုင်သည့်နမူနာများအားလုံးကို နမူနာအချိုးအစားများကြား ကွာခြားချက်များကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဖြူးမှုဖြစ်သည်။

ဆိုလိုသည်မှာ၊ အချိုးအစားကွဲပြားမှု၏နမူနာခွဲဝေရယူခြင်းလုပ်ငန်းစဉ်သည် ပထမ၊ မတူညီသောလူဦးရေနှစ်ခုမှ ဖြစ်နိုင်သည့်နမူနာအားလုံးကို ထုတ်ယူရန်၊ ဒုတိယ၊ ထုတ်ယူလိုက်သောနမူနာတစ်ခုစီ၏ အချိုးအစားကို ဆုံးဖြတ်ရန်၊ နောက်ဆုံးတွင်၊ အားလုံးကြားခြားနားချက်ကို ဆုံးဖြတ်ရန်၊ အချိုးအစား အချိုးအစား ကွာခြားချက်။ လူဦးရေ နှစ်ခု။ သို့မှသာ ဤလုပ်ငန်းဆောင်တာများလုပ်ဆောင်ပြီးနောက် ရရှိသောရလဒ်အစုများသည် အချိုးအစားကွာခြားမှုကို နမူနာဖြန့်ဝေမှုပုံစံဖြစ်စေသည်။

စာရင်းဇယားများတွင်၊ အချိုးအစားနမူနာဖြန့်ဝေမှုတွင် ကွာခြားချက်ကို ကျပန်းရွေးချယ်ထားသောနမူနာနှစ်ခု၏ နမူနာအချိုးအစားများအကြား ကွာခြားမှုသည် လူဦးရေအချိုးအစားကွာခြားချက်နှင့်နီးစပ်သည်ဟု ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန်အသုံးပြုသည်။

➤- အချိုးနမူနာခွဲဝေမှုကို ကြည့်ပါ။

အချိုးအစား ကွာခြားမှုနမူနာ ဖြန့်ဝေခြင်းအတွက် ဖော်မြူလာ

အချိုးအစားနမူနာခွဲဝေမှုတွင် ခြားနားချက်အတွက် ရွေးချယ်ထားသောနမူနာများကို binomial distributions ဖြင့်သတ်မှတ်ထားသည်၊ အကြောင်းမှာ လက်တွေ့ကျသောရည်ရွယ်ချက်များအတွက်၊ အချိုးသည် အောင်မြင်သောဖြစ်ရပ်များ၏ အချိုးအစားဖြစ်ပြီး စုစုပေါင်းလေ့လာတွေ့ရှိချက်အရေအတွက်ဖြစ်သည်။

မည်သို့ပင်ဆိုစေကာမူ၊ ဗဟိုကန့်သတ်သီအိုရီကြောင့်၊ binomial distributions များကို ပုံမှန်ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုများ နှင့် ခန့်မှန်းနိုင်ပါသည်။ ထို့ကြောင့်၊ အချိုးအစားကွဲပြားမှု၏နမူနာခွဲဝေမှုကို အောက်ပါလက္ခဏာများဖြင့် သာမန်ဖြန့်ဖြူးမှုတစ်ခုသို့ ခန့်မှန်းနိုင်သည်-

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

မှတ်ချက်

$n_1\geq30$

၊

$n_2\geq 30$

၊

$n_1p_1\geq5$

၊

$n_2p_2\geq5$

၊

$n_1q_1\geq5$

နှင့်

$n_2q_2\geq5$

ထို့ကြောင့်၊ အချိုးအစားခြားနားချက်၏နမူနာခွဲဝေမှုကို သာမန်ဖြန့်ဖြူးမှုတစ်ခုအဖြစ် ခန့်မှန်းနိုင်သောကြောင့်၊ အချိုးအစားကွာခြားမှုနမူနာခွဲဝေမှု၏ ကိန်းဂဏန်းအချက်အလက်များကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

ရွှေ-

$\widehat{p_i}$

နမူနာအချိုးက i။
$p_i$

လူဦးရေ အချိုးအစားက i။
$q_i$

လူဦးရေ၏ ကျရှုံးမှုဖြစ်နိုင်ချေ i၊

$q_i=1-p_i$

.
$n_i$

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
$Z$

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။

ဤဖော်မြူလာသည် အချိုးအစားအတွက် ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်ဖော်မြူလာနှင့် ဆင်တူသည်။

အချိုးအစားကွဲပြားမှုနမူနာဖြန့်ဝေခြင်း၏ ကွန်ကရစ်ဥပမာ

အချိုးအစားနမူနာဖြန့်ဝေခြင်း၏ ကွာခြားချက်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာဟူသည် အဘယ်နည်းဟူမူကား၊ သဘောတရားကို နားလည်သဘောပေါက်ရန် ပြေလည်အောင်ဖြေရှင်းထားသော ဥပမာအဆင့်ဆင့်ကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။

စက်ရုံနှစ်ခု၏ တိကျမှုကို ခွဲခြမ်းစိတ်ဖြာကြည့်လိုသည်မှာ စက်ရုံတစ်ရုံမှ ထုတ်လုပ်သော အစိတ်အပိုင်းများ၏ 5% သာ ချို့ယွင်းချက်ရှိပြီး အခြားစက်ရုံ၏ ချို့ယွင်းချက်ရာခိုင်နှုန်းမှာ 8% သာရှိသော နည်းလမ်းဖြင့် ထုတ်လုပ်ပါသည်။ ပထမစက်ရုံမှ အစိတ်အပိုင်း 200 နမူနာနှင့် ဒုတိယစက်ရုံမှ အစိတ်အပိုင်း 280 ကို နမူနာယူပါက ပထမစက်ရုံရှိ ချို့ယွင်းချက်ရာခိုင်နှုန်းသည် ဒုတိယစက်ရုံရှိ ချို့ယွင်းချက်ရာခိုင်နှုန်းထက် ပိုများနေခြင်းဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။ ထုတ်လုပ်မှု?

ပြဿနာ၏ အချက်အလက်အားလုံးကို သိရှိရန် အပြီးသတ်ရန်အတွက် အပင်တစ်ခုစီ၏ ကောင်းမွန်စွာထုတ်လုပ်ထားသော အစိတ်အပိုင်းများ၏ အချိုးအစားကို ဦးစွာ တွက်ချက်ပါမည်။

$\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}$

ပထမစက်ရုံရှိ ချို့ယွင်းချက်နှုန်းသည် ဒုတိယစက်ရုံရှိ ချို့ယွင်းချက်နှုန်းထက် ပိုများနေပါက၊ ဆိုလိုသည်မှာ အောက်ပါညီမျှခြင်းမှာ အမှန်ဖြစ်လိမ့်မည်-

$\widehat{p_1}-\widehat{p_2}>0″ title=” Rendered by QuickLaTeX.com” height=” 18″ width=” 89″ style=” vertical-align: -4px;” > ထို့ကြောင့်၊ အချိုးအစားကွာခြားချက်၏နမူနာဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကိုဆုံးဖြတ်ရန်၊ အထက်တွင်ဖော်ပြထားသောအပိုင်းတွင်ဖော်ပြထားသောဖော်မြူလာကိုအသုံးပြုရန်လိုအပ်သည်- <p class=$ $Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}=\cfrac{0-(0,05-0,08)}{\displaystyle\sqrt{\frac{0,05\cdot 0,95}{200}+\frac{0,08\cdot 0,92}{280}}}=1,34$

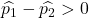
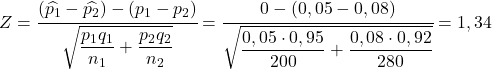
ထို့ကြောင့်၊ ပထမစက်ရုံ၏ ချို့ယွင်းချက်နှုန်းသည် ဒုတိယစက်ရုံ၏ ချို့ယွင်းမှုနှုန်းထက် ပိုများနေခြင်းဖြစ်နိုင်ခြေသည် ကိန်းရှင် Z သည် 1.34 ထက် ပိုများသော ဖြစ်နိုင်ခြေနှင့် ညီမျှသည်-

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 242″ style=” vertical-align: -5px;” > နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် <a href=$ ပုံမှန်ဖြန့်ဖြူးမှုဇယား ရှိ ဆက်စပ်ဖြစ်နိုင်ခြေကို ရှာဖွေရန် လိုအပ်ပြီး ကျွန်ုပ်တို့သည် ပြဿနာကို ဖြေရှင်းပြီးသားဖြစ်လိမ့်မည်-

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 319″ style=” vertical-align: -5px;” > အတိုချုပ်ပြောရလျှင် ပထမစက်ရုံရှိ ချို့ယွင်းချက်အချိုးအစားသည် ဒုတိယစက်ရုံရှိ ချို့ယွင်းချက်အချိုးအစားထက် 9.01% ဖြစ်နိုင်ခြေရှိသည်။ <div style=$ ➤ အဓိပ္ပါယ်မှာ ကွဲပြားမှု၏နမူနာခွဲဝေမှုကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

အချိုးအစားကွာခြားချက်၏နမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။

အချိုးအစား ကွာခြားမှုနမူနာ ဖြန့်ဝေခြင်းအတွက် ဖော်မြူလာ

အချိုးအစားကွဲပြားမှုနမူနာဖြန့်ဝေခြင်း၏ ကွန်ကရစ်ဥပမာ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။