စာရင်းဇယားများတွင် အဆက်ပြတ်ပြင်ဆင်ခြင်း၏ ရိုးရှင်းသော ရှင်းလင်းချက်
ဆက်တိုက်ခွဲဝေမှုကို အနီးစပ်ဆုံး ခွဲခြမ်းစိတ်ဖြာရန် စဉ်ဆက်မပြတ် ဖြန့ ်ဖြူးမှုကို အသုံးပြုလိုသောအခါ ဆက်တိုက် အမှားပြင်ဆင်ခြင်းကို အသုံးချသည်။ ယေဘူယျအားဖြင့်၊ သင်သည် binomial distribution ကို ခန့်မှန်းရန် သာမန်ဖြန့်ဖြူးမှုကို အသုံးပြုလိုသောအခါ ၎င်းကို အသုံးပြုသည်။
စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်မှုဖြစ်နိုင်ခြေသည် p ဖြစ်သောကြောင့် n စမ်းသပ်မှုတွင် x အောင်မြင်မှုရရှိရန် ဖြစ်နိုင်ခြေကို binomial ဖြန့်ဖြူးမှုမှ ပြောပြသည်ကို သတိရပါ။ binomial distribution ဖြင့်ဖြစ်နိုင်ခြေနှင့်ပတ်သက်သောမေးခွန်းများကိုဖြေဆိုရန်၊ binomial distribution calculator ကို ရိုးရိုးရှင်းရှင်းသုံးနိုင်သော်လည်း အဆက်ပြတ်ပြင်ဆင်မှုဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုကို အသုံးပြု၍ ဖြစ်နိုင်ခြေကိုလည်း ခန့်မှန်း နိုင်ပါသည်။
အဆက်ပြတ်ပြင်ဆင်ခြင်းသည် 0.5 ကို discrete x တန်ဖိုးမှ ပေါင်းထည့်ခြင်း သို့မဟုတ် နုတ်ခြင်း အတွက် ပေးထားသော အမည်ဖြစ်သည်။
ဥပမာအားဖြင့်၊ ဒင်္ဂါးပြားတစ်ခုသည် အကြိမ် 100 တွင် အကြိမ် 45 ထက်နည်းသော သို့မဟုတ် ညီမျှသော ခေါင်းပေါ်သို့ ဒင်္ဂါးပြားကျရောက်နိုင်ခြေကို ကျွန်ုပ်တို့ ရှာဖွေလိုသည်ဆိုပါစို့။ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့သည် P(X ≤ 45) ကို ရှာလိုပါသည်။ binomial ဖြန့်ဖြူးမှုကို ခန့်မှန်းရန် ပုံမှန်ဖြန့်ဖြူးမှုကို အသုံးပြုရန်၊ ၎င်းအစား P(X ≤ 45.5) ကို ကျွန်ုပ်တို့ ရှာဖွေမည်ဖြစ်သည်။
အောက်ပါဇယားသည် သင်ရှာဖွေရန်ကြိုးစားနေသည့် ဖြစ်နိုင်ခြေအမျိုးအစားပေါ်မူတည်၍ 0.5 ကို ထည့်ရန် သို့မဟုတ် နုတ်သင့်သည့်အချိန်ကို ပြသသည်-
| binomial distribution ကိုသုံးပါ။ | အဆက်ပြတ်ပြင်ဆင်မှုဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုကို အသုံးပြုခြင်း။ |
|---|---|
| X = 45 | 44.5 < X < 45.5 |
| X ≤ 45 | X < 45.5 |
| X < 45 | X < 44.5 |
| X ≥ 45 | X > 44.5 |
| X > 45 | X > 45.5 |
မှတ်ချက် –
n*p နှင့် n*(1-p) နှစ်ခုလုံးသည် အနည်းဆုံး 5 ဖြစ်သောအခါတွင် binomial distribution ကို ခန့်မှန်းရန် အဆက်မပြတ် တည့်မတ်မှုအား ပုံမှန်ဖြန့်ဖြူးမှုတွင် အသုံးပြုရန် သင့်လျော်ပါသည်။
ဥပမာ n=15 နဲ့ p=0.6 ဆိုပါစို့။ ဒါဆိုရင်:
n*p=15*0.6=9
n*(1-p) = 15* (1 – 0.6) = 15* (0.4) = 6၊
ဤကိန်းဂဏာန်းနှစ်ခုလုံးသည် 5 ထက်ကြီးသည် သို့မဟုတ် ညီမျှသောကြောင့်၊ ဤအခြေအနေတွင် အဆက်ပြတ်ပြင်ဆင်ခြင်းကို လက်ခံနိုင်မည်ဖြစ်သည်။
အောက်ဖော်ပြပါ ဥပမာသည် binomial ဖြန့်ဖြူးမှုကို အနီးစပ်ဆုံးပြုလုပ်ရန် ပုံမှန်ဖြန့်ဖြူးမှုတွင် အဆက်ပြတ်ပြင်ဆင်ခြင်းကို မည်သို့အသုံးပြုရမည်ကို ဖော်ပြသည်။
အဆက်ပြတ်ပြင်ဆင်ခြင်းဆိုင်ရာ အသုံးချပုံဥပမာ
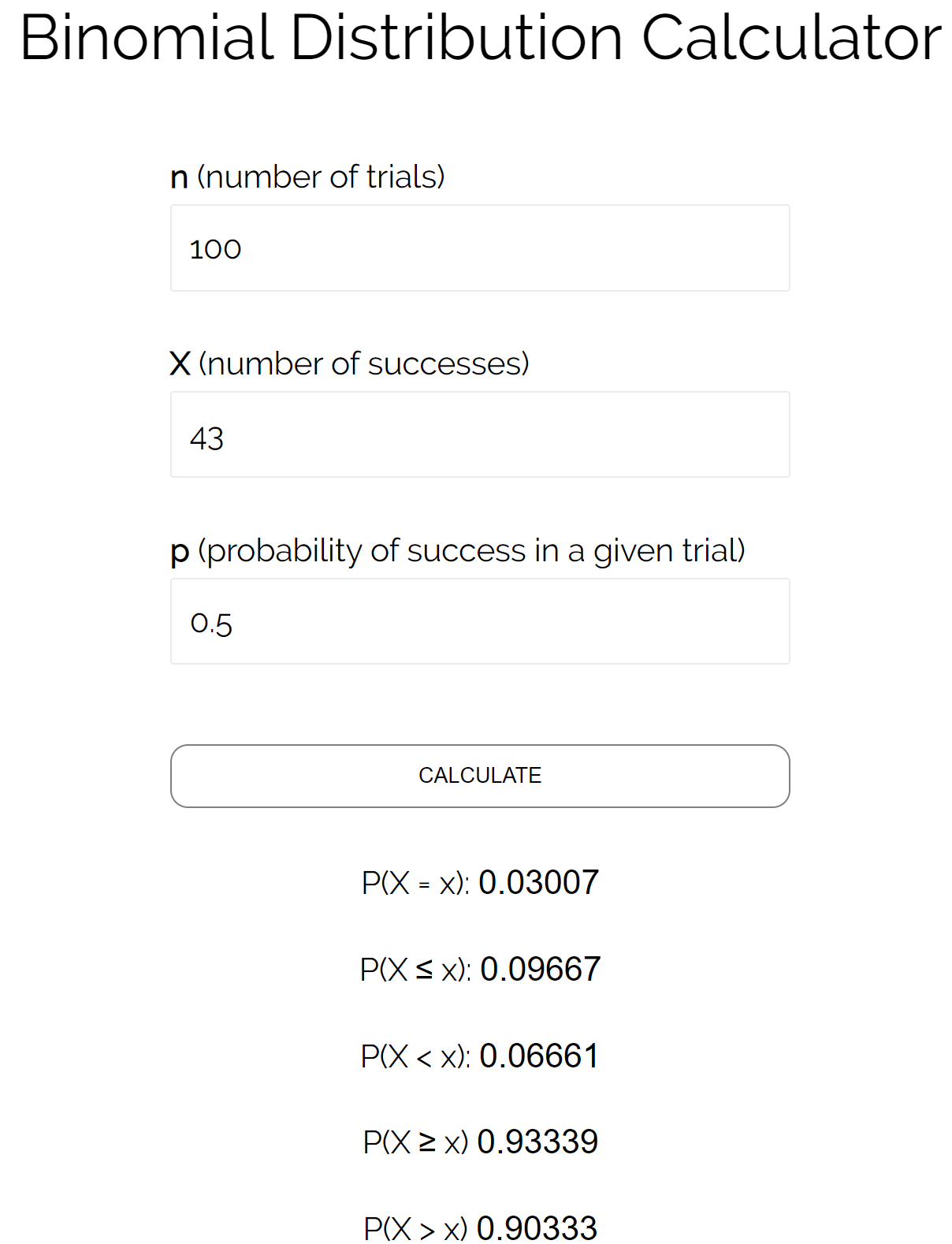
ဒင်္ဂါးပြားတစ်ပြားသည် အကြိမ်ရေ 100 တွင် 43 ဆထက်နည်းသော သို့မဟုတ် ညီမျှသော အကြွေစေ့ခေါင်းပေါ်သို့ ကျရောက်နိုင်ခြေကို ကျွန်ုပ်တို့ သိချင်သည်ဆိုပါစို့။ ဒါဆိုရင်:
n = စမ်းသပ်မှုအရေအတွက် = 100
X = အောင်မြင်သူအရေအတွက် = 43
p = ပေးထားသည့် စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ = 0.50
ခေါင်းများပေါ်တွင် အကြွေစေ့ဆင်းသက်ခြင်း၏ဖြစ်နိုင်ခြေသည် 43 အဆထက်နည်းသည် သို့မဟုတ် 0.09667 ဖြစ်သည်ကို သိရှိနိုင်ရန် ဤနံပါတ်များကို binomial distribution calculator တွင် ချိတ်နိုင်သည်။
ပုံမှန်ဖြန့်ဖြူးမှုသို့ အဆက်ပြတ်ပြင်ဆင်မှုကို အသုံးပြုခြင်းဖြင့် binomial ဖြန့်ဖြူးမှုကို ခန့်မှန်းရန်၊ အောက်ပါအဆင့်များကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
အဆင့် 1- n*p နှင့် n*(1-p) နှစ်ခုစလုံးသည် အနည်းဆုံး 5 ဖြစ်ကြောင်း အတည်ပြုပါ ။
n*p = 100*0.5 = 50
n*(1-p) = 100*(1 – 0.5) = 100*0.5 = 50
ဂဏန်းနှစ်ခုလုံးသည် 5 ထက်ကြီးသည် သို့မဟုတ် ညီမျှသောကြောင့် ကျွန်ုပ်တို့ ဆက်လက်လုပ်ဆောင်နိုင်ပါသည်။
အဆင့် 2- 0.5 ကို ထည့်ရန် သို့မဟုတ် နုတ်ရန် ဆုံးဖြတ်ပါ။
အထက်ပါဇယားကိုရည်ညွှန်း၍ X ≤ 43 ၏ဖြစ်နိုင်ခြေပုံစံဖြင့်အလုပ်လုပ်သောအခါ ကျွန်ုပ်တို့သည် 0.5 ကို ထည့်ရမည် ကိုတွေ့မြင်ရပါသည်။ ထို့ကြောင့် P(X< 43.5) ကိုတွေ့လိမ့်မည်။
အဆင့် 3- binomial distribution ၏ ပျမ်းမျှ (μ) နှင့် စံသွေဖည် (σ) ကို ရှာပါ။
µ = n*p = 100*0.5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
အဆင့် 4- ယခင်အဆင့်တွင်တွေ့ရသော ပျမ်းမျှနှင့် စံသွေဖည်မှုကို အသုံးပြု၍ z-score ကိုရှာပါ။
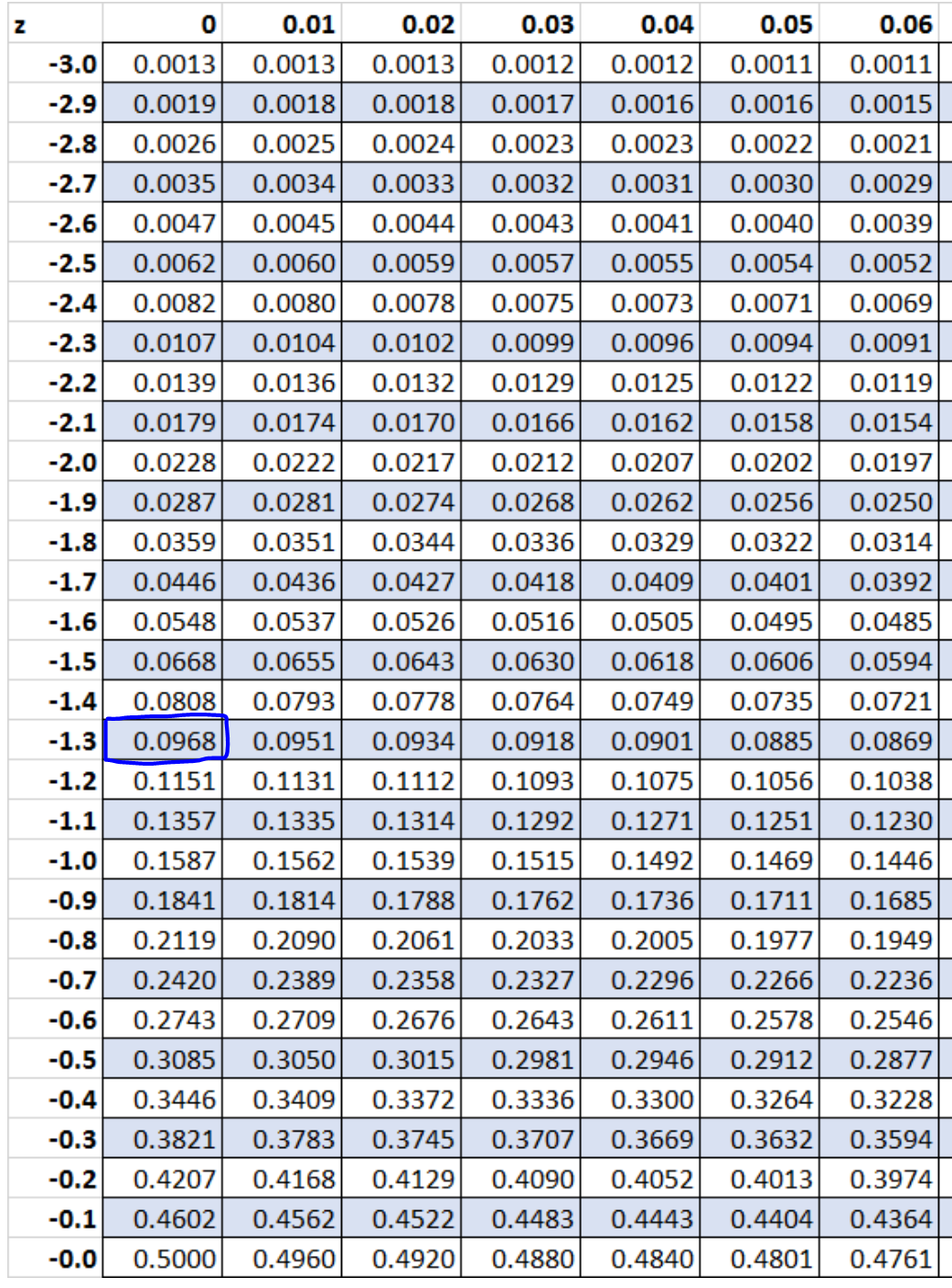
z = (x – μ) / σ = (43.5 – 50) / 5 = -6.5 / 5 = -1.3 ။
အဆင့် 5- z ရမှတ်နှင့် ဆက်စပ်နိုင်ခြေကို ရှာဖွေရန် Z ဇယားကို အသုံးပြုပါ။
ဇယား Z အရ z = -1.3 နှင့် ဆက်စပ်ဖြစ်နိုင်ခြေမှာ 0.0968 ဖြစ်သည်။
ထို့ကြောင့် binomial distribution ကိုအသုံးပြု၍ ကျွန်ုပ်တို့တွေ့ရှိနိုင်သော အတိအကျဖြစ်နိုင်ခြေမှာ 0.09667 ဖြစ်ပြီး၊ ပုံမှန်ဖြန့်ဝေမှုနှင့်အတူ အဆက်ပြတ်ပြင်ဆင်ခြင်းကို အသုံးပြုထားသော ခန့်မှန်းခြေဖြစ်နိုင်ခြေမှာ 0.0968 ဖြစ်သည်။ ဒီတန်ဖိုးနှစ်ခုက အတော်လေးကို ပိတ်နေတယ်။
အဆက်ပြတ်ပြင်ဆင်မှုကို ဘယ်အချိန်မှာ သုံးမလဲ။
ခေတ်မီစာရင်းအင်းဆော့ဖ်ဝဲလ်များ မတည်ရှိမီနှင့် တွက်ချက်မှုများကို ကိုယ်တိုင်လုပ်ဆောင်ရမည်ဖြစ်ပြီး၊ သီးခြားခွဲဝေမှုများပါရှိသည့် ဖြစ်နိုင်ခြေများကို ရှာဖွေရန် အဆက်ပြတ်ပြင်ဆင်မှုများကို မကြာခဏအသုံးပြုခဲ့သည်။ ယနေ့တွင်၊ ကျွန်ုပ်တို့အတွက် ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် ဆော့ဖ်ဝဲလ် သို့မဟုတ် ဂဏန်းတွက်စက်များကို ကျွန်ုပ်တို့အားကိုးနိုင်သောကြောင့် ဖြစ်နိုင်ခြေများကို တွက်ချက်ရာတွင် အဆက်မပြတ်ပြင်ဆင်မှုများသည် အခန်းကဏ္ဍနည်းပါးပါသည်။
ယင်းအစား၊ ၎င်းသည် binomial distribution နှင့် normal distribution အကြား ဆက်နွယ်မှုကို ဖော်ပြရန်နှင့် အဆက်ပြတ်ပြင်ဆင်မှုကို အသုံးပြုခြင်းဖြင့် binomial distribution ကို ခန့်မှန်းရန် ပုံမှန် distribution တစ်ခုအတွက် ဖြစ်နိုင်ကြောင်းပြသရန် ကိန်းဂဏန်းသင်တန်းများတွင် ပါဝင်သော အကြောင်းအရာတစ်ခုဖြစ်သည်။
အဆက်မပြတ်တည့်မတ်မှုဂဏန်းတွက်စက်
အနီးစပ်ဆုံး binomial ဖြစ်နိုင်ခြေများကို ခန့်မှန်းရန်အတွက် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုတွင် ဆက်တိုက်အမှားပြင်ခြင်းကို အလိုအလျောက်အသုံးပြုရန် ဆက်တိုက်ပြင်ဆင်မှုဂဏန်းတွက်စက်ကို အသုံးပြုပါ။