စာရင်းဇယားများတွင် ပျမ်းမျှသည် အဘယ်ကြောင့် အရေးကြီးသနည်း။
တန်ဖိုးအားလုံးကို အငယ်ဆုံးမှ အကြီးဆုံးသို့ စီစဥ်ထားသောအခါ ပျမ်းမျှ သည် ဒေတာအတွဲတစ်ခု၏ အလယ်တန်ဖိုးကို ကိုယ်စားပြုသည်။
ဥပမာအားဖြင့်၊ အောက်ပါဒေတာအတွဲတွင် ပျမ်းမျှသည် 19 ဖြစ်သည်။
ဒေတာအတွဲ- ၃၊ ၄၊ ၁၁၊ ၁၅၊ ၁၉၊ ၂၂၊ ၂၃၊ ၂၃၊ ၂၆
ပျမ်းမျှသည် ဒေတာအစုတစ်ခု၏ 50th ရာခိုင်နှုန်းကိုလည်း ကိုယ်စားပြုသည်။ ဆိုလိုသည်မှာ၊ ဒေတာအတွဲရှိ တန်ဖိုးများ၏ တစ်ဝက်တိတိသည် အလယ်အလတ်အထက်တွင်ရှိပြီး တန်ဖိုးများ၏တစ်ဝက်သည် အောက်တွင်ရှိသည်။
ပျမ်းမျှသည် ဒေတာအတွဲတစ်ခု၏ “ ဗဟို” သည် မည်သည့်နေရာတွင်ရှိသည်ကို အကြံဥာဏ်ပေးသောကြောင့် တွက်ချက်ရန် အရေးကြီးသော မက်ထရစ်တစ်ခုဖြစ်သည်။ ၎င်းသည် ပေးထားသောဒေတာအတွဲတစ်ခုရှိ “ ပုံမှန်” တန်ဖိုးကိုလည်း အကြံဥာဏ်ပေးပါသည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် မြို့တစ်မြို့၌ မတူညီသော အိမ် 10,000 ၏ အရောင်းစျေးနှုန်းများ ပါဝင်သော ဒေတာအစုံရှိသည် ဆိုကြပါစို့။

ကုန်ကြမ်းဒေတာ အတန်းနှင့် အတန်းများကို ကြည့်မည့်အစား၊ ထိုမြို့ရှိ အိမ်များ၏ ပျမ်းမျှရောင်းဈေးကို လျင်မြန်စွာ နားလည်ရန် ပျမ်းမျှတန်ဖိုးကို တွက်ချက်နိုင်ပါသည်။
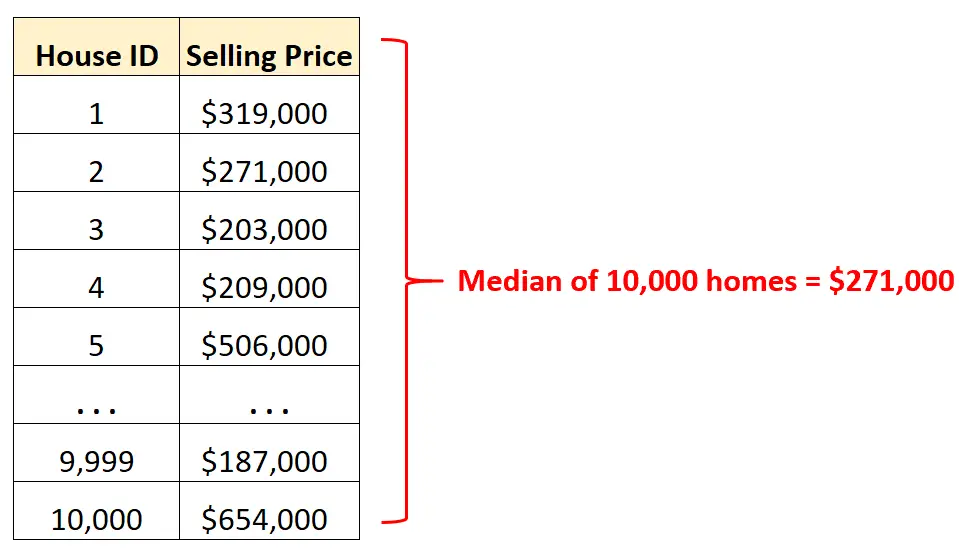
ပျမ်းမျှရောင်းဈေးမှာ $271,000 ဖြစ်သည်ကို သိရှိထားသောကြောင့် အိမ် 10,000 ၏ ထက်ဝက်တိတိကို ထိုပမာဏထက် ပိုရောင်းရပြီး ကျန်တစ်ဝက်မှာ သက်သာကြောင်း ကျွန်ုပ်တို့သိပါသည်။
၎င်းသည် ဤမြို့ရှိ အိမ်များ၏ “ ပုံမှန်” ရောင်းစျေးကို အကြံဥာဏ်ပေးပါသည်။
အလယ်အလတ်ကို ဘယ်အချိန်မှာ သုံးမလဲ။
ဒေတာအစုံများကို ခွဲခြမ်းစိတ်ဖြာသောအခါ၊ ကျွန်ုပ်တို့သည် ဗဟိုတန်ဖိုးသည် မည်သည့်နေရာတွင်ရှိသည်ကို နားလည်လိုကြသည်။
စာရင်းဇယားများတွင်၊ ဒေတာအတွဲတစ်ခု၏ဗဟိုကို တိုင်းတာရန် ကျွန်ုပ်တို့အသုံးပြုလေ့ရှိသော မက်ထရစ်နှစ်ခုရှိသည်။
- ဆိုလိုသည်မှာ ဒေတာအစုတစ်ခုရှိ ပျမ်းမျှတန်ဖိုး
- Median- ဒေတာအတွဲတစ်ခုရှိ ပျမ်းမျှတန်ဖိုး
အလယ်အလတ်သည် အောက်ပါအခြေအနေများတွင် ပိုမိုအသုံးဝင်သော အတိုင်းအတာတစ်ခုဖြစ်ကြောင်း တွေ့ရှိရပါသည်။
- ဖြန့်ဝေမှု အချိုးမညီ သောအခါ။
- ဖြန့်ဖြူးသည့်အခါတွင် အစွန်းထွက်များပါရှိသည်။
ယင်းကို သရုပ်ဖော်ရန် အောက်ပါ ဥပမာနှစ်ခုကို သုံးသပ်ကြည့်ပါ။
ဥပမာ 1- လွဲမှားသော ဖြန့်ဖြူးမှု၏ ပျမ်းမျှအား တွက်ချက်ခြင်း။
အချို့သောမြို့များတွင် နေထိုင်သူများအတွက် အောက်ပါလစာများ ခွဲဝေမှုကို ထည့်သွင်းစဉ်းစားပါ။

ဖြန့်ဖြူးမှုသည် ညာဘက်သို့ လွဲသွားသောကြောင့် ပျမ်းမျှအားဖြင့် နေထိုင်သူ၏ “ ပုံမှန်” လစာသည် ပျမ်းမျှထက် ပိုကောင်းသည်ကို ထင်ဟပ်ပါသည်။
ဆိုလိုသည်မှာ ဖြန့်ဖြူးမှု၏ညာဘက်ခြမ်းရှိ မြင့်မားသောလုပ်ခလစာသည် ဖြန့်ဖြူးမှု၏ဗဟိုမှ ဆိုလိုရင်းကို တွန်းပို့ခြင်းဖြစ်သည်။
ဤဥပမာတွင်၊ ပျမ်းမျှလစာမှာ $47,000 ဖြစ်ပြီး ပျမ်းမျှလစာမှာ $32,000 ဖြစ်သည်။ ပျမ်းမျှသည် ဤမြို့၏ ပုံမှန်လစာ၏ ကိုယ်စားပြုမှု ပိုများသည်။
ဥပမာ 2- outliers များရှေ့တွင် အလယ်အလတ်ကို တွက်ချက်ခြင်း။
အချို့သောလမ်းပေါ်ရှိ အိမ်များ၏စတုရန်းပုံများကိုပြသသည့် အောက်ပါဂရပ်ကို သုံးသပ်ကြည့်ပါ-

ပျမ်းမျှအား အလယ်အလတ်မရှိသော်လည်း အလွန်ကြီးမားသောအိမ်အနည်းငယ်မှ ကြီးကြီးမားမားလွှမ်းမိုးထားသည်။
အလယ်အလတ်သည် ထိုလမ်းပေါ်ရှိ အိမ်တစ်အိမ်၏ “ ပုံမှန်” စတုရန်းပုံအား ပျမ်းမျှထက် သာလွန်သူများ၏ လွှမ်းမိုးမှုမခံရသောကြောင့် အလယ်အလတ်သည် ပိုမိုကောင်းမွန်သောအလုပ်ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။
အကျဉ်းချုပ်
ဤဆောင်းပါးတွင် ဖော်ပြထားသော အဓိကအချက်များကို အကျဉ်းချုပ် အကျဉ်းချုပ် ဖော်ပြထားပါသည်။
- ပျမ်းမျှသည် ဒေတာအတွဲတစ်ခုရှိ အလယ်တန်ဖိုးကို ကိုယ်စားပြုသည်။
- အလယ်အလတ်သည် အရေးကြီးသောကြောင့် ဒေတာအစုတစ်ခုတွင် ဗဟိုတန်ဖိုးသည် မည်သည့်နေရာတွင် ရှိနေသည်ကို အကြံဥာဏ်ပေးသောကြောင့် ဖြစ်သည်။
- ဖြန့်ဖြူးမှုတစ်ခုအား လွဲချော်နေပြီး/သို့မဟုတ် အစွန်းအထင်းများပါရှိသည့် ပျမ်းမျှထက် တွက်ချက်ရန် ပျမ်းမျှသည် ပိုမိုအသုံးဝင်ပါသည်။
ထပ်လောင်းအရင်းအမြစ်များ
ကွန်ကရစ်ဥပမာများ- Mean၊ Median နှင့် Mode ကိုအသုံးပြုခြင်း။
Mean vs. အလယ်အလတ်- ဥပမာများဖြင့်
စာရင်းဇယားများတွင် မုဒ်သည် အဘယ်ကြောင့် အရေးကြီးသနည်း။