အံဝင်ခွင်ကျ အရည်အသွေး
ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် အံဝင်ခွင်ကျရှိမှု မည်သည်တို့ကို ရှင်းပြထားသည်။ အလားတူ၊ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံ၏ အံဝင်ခွင်ကျမှုကို မည်သို့တိုင်းတာရမည်ကို ပြသပြီး ထို့အပြင်၊ အံဝင်ခွင်ကျဖြစ်ခြင်း၏ ဖြေရှင်းနည်းကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။
အံဝင်ခွင်ကျကောင်းမှုဆိုတာ ဘာလဲ။
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ အံဝင်ခွင်ကျကောင်းမွန်မှုသည် ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာနမူနာနှင့် မည်မျှကိုက်ညီမှုကောင်းသည်။ တစ်နည်းဆိုရသော် ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အံဝင်ခွင်ကျကောင်းမွန်မှုသည် အကဲခတ်မှုအစုများနှင့် ဆုတ်ယုတ်မှုမှတစ်ဆင့် ရရှိသောတန်ဖိုးများကြားတွင် ပေါင်းစပ်မှုအဆင့်ကို ရည်ညွှန်းသည်။
ထို့ကြောင့်၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အံဝင်ခွင်ကျကောင်းမှု ပိုမိုကောင်းမွန်လေ၊ လေ့လာနေသည့် အချက်အလက်ကို ရှင်းပြလေလေ ပိုကောင်းလေဖြစ်သည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းဆိုင်ရာ စံနမူနာနှင့် ပိုမိုကောင်းမွန်သော အံဝင်ခွင်ကျဖြစ်မှုကို လိုလားပါသည်။
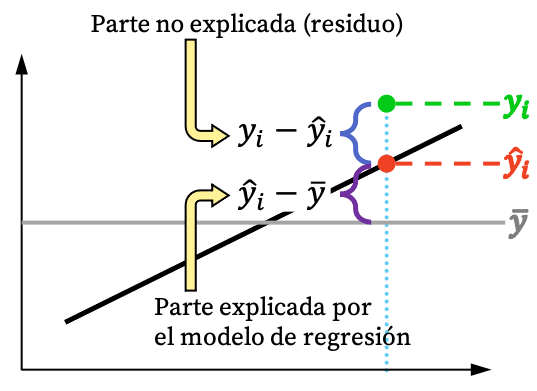
အထက်ပုံမှ သင်မြင်နိုင်သည်အတိုင်း၊ ပုံမှန်အားဖြင့် လေ့လာမှုတစ်ခု၏တန်ဖိုးကို ဆုတ်ယုတ်မှုပုံစံဖြင့် အပြည့်အဝရှင်းပြ၍မရပါ။ သို့သော် ယုတ္တိနည်းအရ၊ ဒေတာအတွဲမှ ဆုတ်ယုတ်မှုပုံစံကို ပိုမိုရှင်းပြနိုင်လေ၊ မော်ဒယ်သည် ပိုမိုကောင်းမွန်လေဖြစ်သည်။ အတိုချုပ်အားဖြင့်၊ ကျွန်ုပ်တို့သည် တတ်နိုင်သမျှ တင်းကျပ်သော ဆုတ်ယုတ်မှုပုံစံကို စိတ်ဝင်စားပါသည်။
ဆုတ်ယုတ်မှုပုံစံ၏ အံဝင်ခွင်ကျကောင်းမှု
ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အံဝင်ခွင်ကျရှိမှုကို ဆုံးဖြတ်ရန်၊ ပုံမှန်အားဖြင့်၊ တစ်ခုသည် ဆုတ်ယုတ်မှုပုံစံဖြင့် ရှင်းပြထားသော ရာခိုင်နှုန်းကို ညွှန်ပြသည့် ကိန်းဂဏန်းကိန်းကိန်းတစ်ခုဖြစ်သည့် ကိန်းဂဏန်းကိန်းဂဏန်းကို အသုံးပြုသည် ။ ထို့ကြောင့်၊ မော်ဒယ်တစ်ခု၏ ဆုံးဖြတ်မှုကိန်းဂဏန်း မြင့်မားလေ၊ မော်ဒယ်သည် ဒေတာနမူနာသို့ ပိုမိုကောင်းမွန်စွာ လိုက်လျောညီထွေရှိလေလေဖြစ်သည်။
![]()
သို့ရာတွင်၊ regression model တစ်ခုတွင် ကိန်းရှင်များ များလေလေ၊ ၎င်း၏ အဆုံးအဖြတ်၏ ဖော်ကိန်း မြင့်မားလေ ဖြစ်သည်ကို သတိပြုသင့်သည်။ ဤအကြောင်းကြောင့် မော်ဒယ်တစ်ခု၏ အံဝင်ခွင်ကျကောင်းမှုကို တိုင်းတာရန် ချိန်ညှိထားသော ကိန်းဂဏန်းကို မကြာခဏ အသုံးပြုပါသည်။ ချိန်ညှိသတ်မှတ်ခြင်းဆိုင်ရာ ကိန်းဂဏန်းသည် ဆုတ်ယုတ်မှုပုံစံဖြင့် ရှင်းပြထားသည့် ရာခိုင်နှုန်းကို ညွှန်ပြသည့် ယခင်ကိန်းဂဏန်း၏ ကွဲလွဲမှုတစ်ခုဖြစ်ပြီး မော်ဒယ်တွင်ပါရှိသော ရှင်းပြကိန်းရှင်တစ်ခုစီအတွက် အပြစ်ပေးသည်။
![]()
ထို့ကြောင့် မော်ဒယ်နှစ်ခုတွင် ပါဝင်သော variable အရေအတွက်ကို ထည့်သွင်းစဉ်းစားသောကြောင့် မော်ဒယ်နှစ်ခုကို မတူညီသော variable အများအပြားဖြင့် နှိုင်းယှဉ်ရန် ချိန်ညှိထားသော coefficient of determination ကို အသုံးပြုခြင်းက ပိုကောင်းပါတယ်။
နောက်ဆုံးအနေဖြင့်၊ ယခင် coefficients နှစ်ခု၏ တန်ဖိုးများကို အများအားဖြင့် အသုံးပြုသော်လည်း regression model တစ်ခု၏ အံဝင်ခွင်ကျ ကောင်းမွန်မှုကို တိုင်းတာရန်အတွက် Chi-square test ကိုလည်း အသုံးပြုနိုင်ကြောင်း သတိပြုသင့်သည်။
အံဝင်ခွင်ကျ ခိုင်မာသော ဥပမာ
နောက်ဆုံးတွင်၊ ဤကိန်းဂဏန်းဆိုင်ရာအယူအဆကို ပေါင်းစပ်ထည့်သွင်းရန် ညှိနှိုင်းမှုအရည်အသွေးကို ပြေလည်အောင်ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။
- တူညီသောဒေတာစီးရီးဖြင့်၊ မတူညီသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံနှစ်ခုကိုလုပ်ဆောင်သည်၊ အောက်ပါဇယားတွင်သင်တွေ့နိုင်သည့်ရလဒ်များ။ ဘယ်မော်ဒယ်ကို သုံးဖို့ အကောင်းဆုံးလဲ။
| ဆုတ်ယုတ်မှုပုံစံ ၁ | ဆုတ်ယုတ်မှုပုံစံ ၂ | |
|---|---|---|
| အဆုံးအဖြတ်ပေးသောကိန်း | 57% | 64% |
| ချိန်ညှိဆုံးဖြတ်ခြင်း ကိန်းဂဏန်း | 49% | 43% |
| ရှင်းလင်းချက် ကိန်းရှင် အရေအတွက် | ၃ | ၇ |
ဤကိစ္စတွင်၊ မော်ဒယ်နှစ်ခုလုံးသည် မျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံများ၏ ယခင်ယူဆချက်များကို ကျေနပ်သည်ဟု ကျွန်ုပ်တို့ယူဆပြီး ထို့ကြောင့်၊ မော်ဒယ်များ၏ အံဝင်ခွင်ကျကောင်းမှုကို ပိုင်းခြားစိတ်ဖြာရန်သာ လိုအပ်ပါသည်။
Regression model 2 သည် regression model 1 ထက် ပိုမိုမြင့်မားသော ဆုံးဖြတ်နိုင်စွမ်းရှိသောကြောင့် ၎င်းသည် data sample ကို ပိုမိုကောင်းမွန်စွာရှင်းပြနိုင်သောကြောင့် ဦးစားပေးတစ်ခုအနေဖြင့် ပိုကောင်းသော regression model တစ်ခုဖြစ်သည်။
သို့သော် Regression Model 2 တွင် မော်ဒယ်တွင် သီးခြား ကိန်းရှင် 7 ခု ရှိပြီး Regression Model 1 တွင် 3 သာ ရှိသည်။ ထို့ကြောင့် Model 2 သည် ပထမမော်ဒယ်ထက် များစွာ ပိုမိုရှုပ်ထွေးပြီး အဓိပ္ပာယ်ဖွင့်ဆိုရန် ခက်ခဲမည်ဖြစ်သည်။
ထို့အပြင်၊ မော်ဒယ်ရှိ ကိန်းရှင်အရေအတွက်များကို ထည့်သွင်းစဉ်းစားသည့် ချိန်ညှိထားသော ကိန်းဂဏန်းများကို ကြည့်လျှင်၊ ဆုတ်ယုတ်မှုပုံစံ 1 သည် ဆုတ်ယုတ်မှုပုံစံ 2 ထက် ချိန်ညှိထားသော ကိန်းဂဏန်းပိုမိုမြင့်မားသော ဆုံးဖြတ်ချက်တစ်ခုဖြစ်သည်။
နိဂုံးချုပ်အနေဖြင့်၊ regression model 1 ကို အသုံးပြုခြင်းသည် ပိုကောင်းသော်လည်း၊ ၎င်း၏ ချိန်ညှိထားသော ကိန်းဂဏန်းသည် regression model 2 ထက် မြင့်မားသောကြောင့် ဖြစ်သည်။ regression model 2 တွင် ပိုမိုမြင့်မားသော ချိန်ညှိမထားသော coefficient ရှိသည်၊ ၎င်းတို့သည် regression တွင် နောက်ထပ် variable များစွာပါ၀င်သောကြောင့် ဖြစ်ပါသည်။ မော်ဒယ် 1. မော်ဒယ်သည် ပြောကြားသော coefficient ၏တန်ဖိုးကို တိုးစေသော်လည်း မော်ဒယ်၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်ကို ပိုမိုခက်ခဲစေကာ အမှန်ပင်၊ ၎င်းသည် တန်ဖိုးအသစ်တစ်ခု၏ ခန့်မှန်းမှုကို ပိုဆိုးစေသည်။
မတူညီသောကိန်းရှင်အရေအတွက်များနှင့် မော်ဒယ်များကို နှိုင်းယှဉ်ရန်၊ မော်ဒယ်တွင်ထည့်သွင်းထားသော variable တစ်ခုစီအတွက် အပြစ်ပေးသောကြောင့် ချိန်ညှိထားသော ကိန်းဂဏန်းကို အသုံးပြုခြင်းသည် အကောင်းဆုံးဖြစ်သည်။ ဤဥပမာတွင် သင်တွေ့ခဲ့သည့်အတိုင်း၊ မညှိမထားသောကိန်းဂဏန်းအရ ဆုတ်ယုတ်မှုပုံစံ 2 သည် ပိုကောင်းသည်၊ သို့သော်၊ ချိန်ညှိထားသောကိန်းဂဏန်းအားဖြင့် ဆုတ်ယုတ်မှုပုံစံ 1 သည် အမှန်တကယ်ပိုကောင်းကြောင်း ကျွန်ုပ်တို့သိနိုင်သည်။