လမ်းညွှန်ချက်အပြည့်အစုံ- 2×2 factorial ဒီဇိုင်း

2 × 2 Factorial ဒီဇိုင်း သည် သုတေသီများအား အမှီအခိုကင်းသော variable နှစ်ခု ( အဆင့် နှစ်ဆင့်တစ်ခုစီ) ၏ အကျိုးသက်ရောက်မှုများကို သုတေသီများအား နားလည်နိုင်စေမည့် စမ်းသပ်ဒီဇိုင်းအမျိုးအစားတစ်ခုဖြစ်သည်။

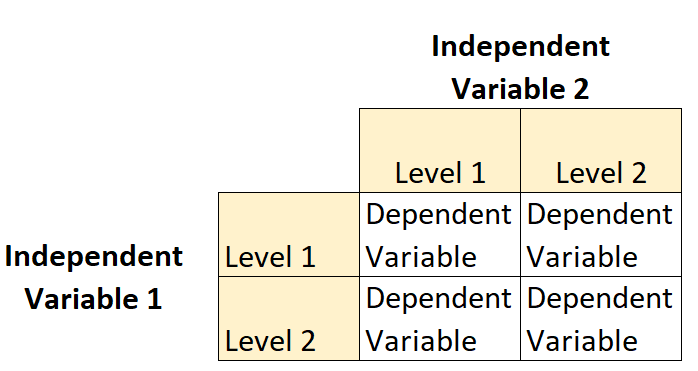
ဥပမာအားဖြင့်၊ ရုက္ခဗေဒပညာရှင်သည် အပင်မျိုးစိတ်တစ်ခု၏ ကြီးထွားမှုအပေါ် နေရောင်ခြည် (အနိမ့်ဆုံး သို့မဟုတ် မြင့်မား) နှင့် ရေလောင်းအကြိမ်ရေ (နေ့စဉ် သို့မဟုတ် အပတ်စဉ်) ၏အကျိုးသက်ရောက်မှုကို နားလည်လိုသည်ဆိုပါစို့။

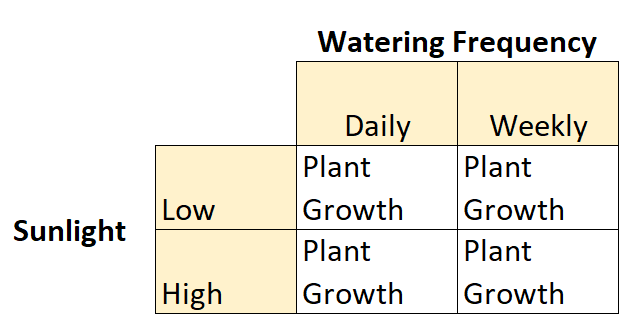
ဤသည်မှာ 2×2 Factorial Design ၏ ဥပမာတစ်ခုဖြစ်ပြီး တစ်ခုစီတွင် အဆင့်နှစ်ဆင့်ရှိသည့် သီးခြားကွဲပြားချက်နှစ်ခုရှိသောကြောင့်၊

• အမှီအခိုကင်းသော Variable နံပါတ် 1- နေရောင်ခြည်
  • အဆင့်များ- အနိမ့်၊ အမြင့်
• အမှီအခိုကင်းသော ကိန်းရှင်နံပါတ် 2- ရေလောင်းအကြိမ်ရေ
  • အဆင့်များ- နေ့စဉ်၊ အပတ်စဉ်

အပင်ကြီးထွားမှုအပေါ် မူတည်၍ ပြောင်းလဲနိုင်သော ကိန်းရှင်တစ်ခုရှိသည်။

2×2 factorial ဒီဇိုင်းတစ်ခု၏ ရည်ရွယ်ချက်

2×2 factorial ဒီဇိုင်းသည် အောက်ပါအကျိုးသက်ရောက်မှုများကို ခွဲခြမ်းစိတ်ဖြာနိုင်စေသည်-

ပင်မအကျိုးသက်ရောက်မှုများ- ၎င်းတို့သည် အမှီအခိုကင်းသော ကိန်းရှင်တစ်ခုတွင် မှီခိုနေသောကိန်းရှင်အပေါ် သက်ရောက်မှုများဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ယခင်အခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် အောက်ပါအဓိကအကျိုးသက်ရောက်မှုများကို ပိုင်းခြားစိတ်ဖြာနိုင်သည်-

• အပင်ကြီးထွားမှုအပေါ် နေရောင်ခြည်၏ အဓိကသက်ရောက်မှု။
  • နေရောင်ခြည်နည်းသော အပင်အားလုံး၏ ပျမ်းမျှကြီးထွားမှုကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်။
  • နေရောင်ခြည် မြင့်မားစွာရရှိသော အပင်အားလုံး၏ ပျမ်းမျှကြီးထွားမှုကို ကျွန်ုပ်တို့ တွေ့ရှိနိုင်သည်။
• အပင်ကြီးထွားမှုအပေါ် ရေလောင်းကြိမ်နှုန်း၏ အဓိကအကျိုးသက်ရောက်မှု။
  • နေ့စဥ်ရေလောင်းသော အပင်အားလုံး၏ ပျမ်းမျှကြီးထွားမှုကို ကျွန်ုပ်တို့ တွေ့ရှိနိုင်သည်။
  • တစ်ပတ်လျှင် ရေလောင်းသော အပင်အားလုံး၏ ပျမ်းမျှကြီးထွားနှုန်းကို ကျွန်ုပ်တို့ တွေ့ရှိနိုင်သည်။

အပြန်အလှန်အကျိုးသက်ရောက်မှုများ- အမှီအခိုကင်းသောကိန်းရှင်တစ်ခု၏အကျိုးသက်ရောက်မှုသည်အခြားအမှီအခိုကင်းသောကိန်းရှင်၏အဆင့်အပေါ်မူတည်သောအခါတွင်ဖြစ်ပေါ်ပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ယခင်အခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် အောက်ပါ အပြန်အလှန်အကျိုးသက်ရောက်မှုများကို ပိုင်းခြားစိတ်ဖြာနိုင်သည်-

• အပင်ကြီးထွားမှုအပေါ် နေရောင်ခြည်၏အကျိုးသက်ရောက်မှုသည် ရေလောင်းသည့်အကြိမ်ရေအပေါ် မူတည်ပါသလား။
• အပင်ကြီးထွားမှုအပေါ် ရေလောင်းအကြိမ်ရေ၏ အကျိုးသက်ရောက်မှုသည် နေရောင်ခြည်ပေါ်တွင် မူတည်ပါသလား။

အဓိကအကျိုးသက်ရောက်မှုများနှင့် အပြန်အလှန်အကျိုးသက်ရောက်မှုများကို မြင်ယောင်ကြည့်ပါ။

ကျွန်ုပ်တို့သည် 2 × 2 Factorial ဒီဇိုင်းကို အသုံးပြုသောအခါ၊ မှီခိုသောကိန်းရှင်အပေါ် လွတ်လပ်သောကိန်းရှင်များ၏ အကျိုးသက်ရောက်မှုများကို ပိုမိုကောင်းမွန်စွာနားလည်ရန် မကြာခဏ ဂရပ်ဖစ်ပါသည်။

ဥပမာအားဖြင့်၊ အောက်ပါဇာတ်ကွက်ကို သုံးသပ်ကြည့်ပါ။

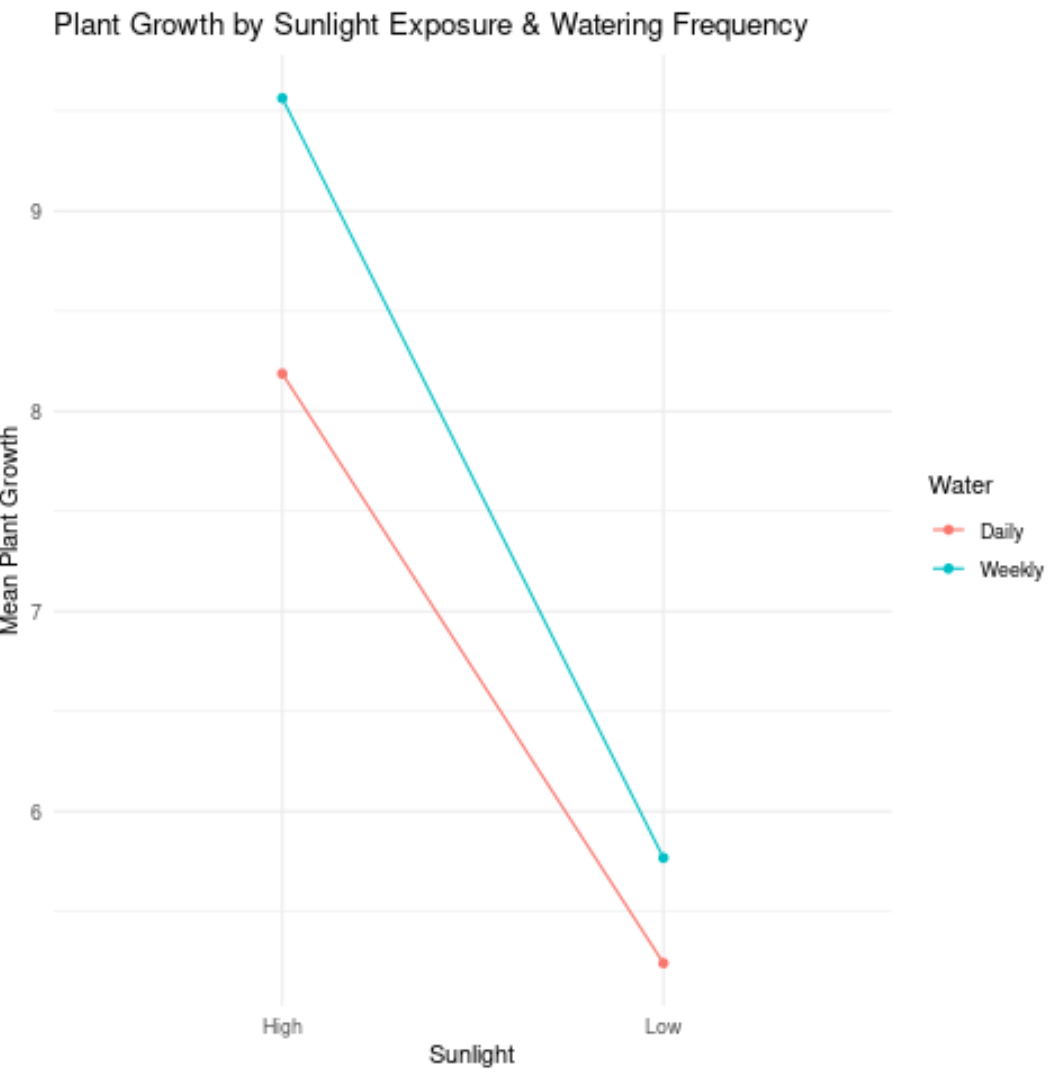
ဤသည်မှာ ဇာတ်ကွက်အတွင်းရှိ တန်ဖိုးများကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• ပြင်းထန်သောနေရောင်ခြည်နှင့်နေ့စဉ်ရေလောင်းသောအပင်များ၏ပျမ်းမျှကြီးထွားမှုသည် 8.2 လက်မခန့်ဖြစ်သည်။
• နေရောင်ခြည်နှင့် အပတ်စဉ်ရေလောင်းသည့် အပင်များ၏ ပျမ်းမျှကြီးထွားနှုန်းမှာ ၉.၆ လက်မခန့်ဖြစ်သည်။
• နေအနည်းအကျဉ်းနှင့် နေ့စဉ်ရေလောင်းသည့် အပင်များ၏ ပျမ်းမျှကြီးထွားနှုန်းမှာ ၅.၃ လက်မခန့်ဖြစ်သည်။
• နေနည်းပြီး အပတ်စဉ် ရေလောင်းပေးသော အပင်များ၏ ပျမ်းမျှကြီးထွားနှုန်းမှာ ၅.၈ လက်မခန့်ဖြစ်သည်။

အမှီအခိုကင်းသော ကိန်းရှင်နှစ်ခုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုရှိမရှိ ဆုံးဖြတ်ရန်၊ မျဉ်းများသည် အပြိုင်ဖြစ်နေခြင်းရှိ၊

• ကွက်ကွက်၏မျဉ်းနှစ်ကြောင်းသည် မျဉ်းပြိုင်ဖြစ်ပါက အပြန်အလှန်အကျိုးသက်ရောက်မှု မရှိပါ။
• ကွက်ကွက်၏မျဉ်းနှစ်ကြောင်းသည် မျဉ်းပြိုင် မဟုတ်ပါ က အပြန်အလှန်အကျိုးသက်ရောက်မှုရှိပါသည်။

ယခင်ဂရပ်တွင်၊ မျဉ်းနှစ်ကြောင်းသည် အကြမ်းဖျင်းအားဖြင့် မျဉ်းပြိုင်ဖြစ်သောကြောင့် ရေလောင်းကြိမ်နှုန်းနှင့် နေရောင်ခြည်ထိတွေ့မှုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှု မရှိနိုင်ပါ။

သို့သော် အောက်ပါဇာတ်ကွက်ကို သုံးသပ်ကြည့်ပါ။

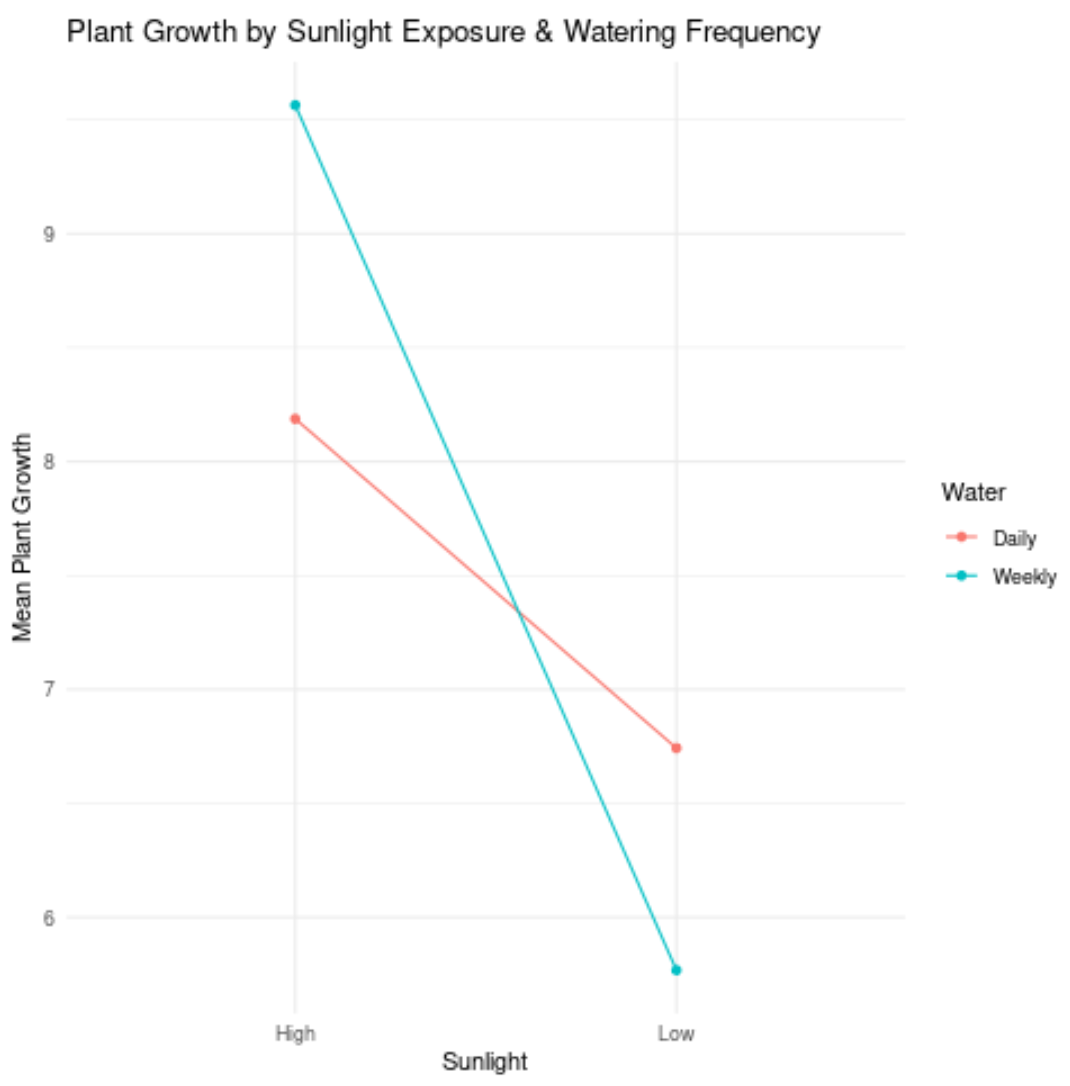
မျဉ်းနှစ်ကြောင်းသည် လုံး၀မျဉ်းပြိုင်မဟုတ်ပါ (တကယ်တော့ ၎င်းတို့ကြားတွင် အပြန်အလှန်သက်ရောက်မှုရှိနိုင်သည်ဟု ညွှန်ပြသောအားဖြင့် ၎င်းတို့က ဖြတ်တောက်ထားသည်။)

ဥပမာအားဖြင့်၊ ဆိုလိုသည်မှာ အပင်ကြီးထွားမှုအပေါ် နေရောင်ခြည်၏အကျိုးသက်ရောက်မှုသည် ရေလောင်းသည့်အကြိမ်ရေပေါ်တွင် မူတည်သည်ဟု ဆိုလိုသည်။

တစ်နည်းဆိုရသော် နေရောင်ခြည်နှင့် ရေလောင်းသည့်ကြိမ်နှုန်းသည် အပင်ကြီးထွားမှုကို သီးခြားမထိခိုက်စေပါ။ ယင်းအစား၊ အမှီအခိုကင်းသော variable နှစ်ခုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှု ရှိသည်။

2×2 factorial ဒီဇိုင်းကို ခွဲခြမ်းစိတ်ဖြာနည်း

Plotting averages သည် အမှီအခိုကင်းသော variable များပေါ်တွင် မှီခိုနေသော variable ပေါ်တွင်ရှိသော အကျိုးသက်ရောက်မှုများကို စစ်ဆေးရန် အမြင်အာရုံနည်းလမ်းတစ်ခုဖြစ်သည်။

သို့ရာတွင်၊ သီးခြားကိန်းရှင်များသည် မှီခိုကိန်းရှင်နှင့် ကိန်းဂဏန်းအချက်အချာကျသော ဆက်နွယ်မှုရှိမရှိ တရားဝင်စမ်းသပ်ရန် နှစ်လမ်း ANOVA ကိုလည်း လုပ်ဆောင်နိုင်သည်။

ဥပမာအားဖြင့်၊ အောက်ဖော်ပြပါကုဒ်သည် ကျွန်ုပ်တို့၏ယူဆချက်စက်ရုံတွင် R တွင် နှစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ဤသည်မှာ ANOVA ရလဒ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံဖြစ်သည်။

• နေရောင်ခြည်နှင့်ဆက်စပ်သော p-တန်ဖိုးသည် 0.005 ဖြစ်သည်။ ဤကိန်းဂဏန်းသည် 0.05 ထက်နည်းသောကြောင့် နေရောင်ခြည်နှင့်ထိတွေ့မှုသည် အပင်ကြီးထွားမှုအပေါ် ကိန်းဂဏန်းအရ သိသာထင်ရှားသောအကျိုးသက်ရောက်မှုကို ဆိုလိုသည်။
• ရေနှင့်ဆက်စပ်နေသော p-တန်ဖိုးသည် 0.028 ဖြစ်သည်။ ဤကိန်းဂဏန်းသည် 0.05 ထက်နည်းသောကြောင့် ရေလောင်းသည့်အကြိမ်ရေသည်လည်း အပင်ကြီးထွားမှုအပေါ် ကိန်းဂဏန်းအရ သိသာထင်ရှားသောအကျိုးသက်ရောက်မှုရှိကြောင်း ဆိုလိုသည်။
• နေရောင်ခြည်နှင့်ရေအကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုအတွက် p-တန်ဖိုးသည် 0.156 ဖြစ်သည်။ ဤကိန်းဂဏန်းသည် 0.05 ထက်မနည်းသောကြောင့် နေရောင်ခြည်နှင့် ရေကြားတွင် အပြန်အလှန်သက်ရောက်မှုမရှိဟု ဆိုလိုသည်။

ထပ်လောင်းအရင်းအမြစ်များ

လမ်းညွှန်ချက်အပြည့်အစုံ- 2×3 စက်ရုံအလုပ်ရုံ ဒီဇိုင်း
လွတ်လပ်သော ကိန်းရှင်၏ အဆင့်များသည် အဘယ်နည်း။
အမှီအခိုကင်းသော သို့မဟုတ် မှီခိုသော ကိန်းရှင်များ
Factorial ANOVA ဆိုတာဘာလဲ။