Phi coefficient- အဓိပ္ပါယ်နှင့် ဥပမာများ

Phi coefficient (ရံဖန်ရံခါ ပျမ်းမျှစတုရန်းအခြေအနေဆိုင်ရာကိန်းဂဏန်း ဟု ခေါ်သည်) သည် ဒွိကိန်းရှင်နှစ်ခုကြား ပေါင်းစည်းခြင်း၏ အတိုင်းအတာတစ်ခုဖြစ်သည်။

ကျပန်းပြောင်းလဲနိုင်သော x နှင့် y နှစ်ခုအတွက် ပေးထားသော 2×2 ဇယားတစ်ခုအတွက်

Phi coefficient ကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

ဥပမာ- Phi coefficient တွက်ချက်ခြင်း။

နိုင်ငံရေး ပါတီတစ်ခုအတွက် ဦးစားပေးမှုတွင် ကျား၊မ ဆက်စပ်မှု ရှိ၊ မရှိ သိလိုသည်ဆိုပါစို့။ ကျွန်ုပ်တို့သည် မဲဆန္ဒရှင် ၂၅ ဦး၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ ၎င်းတို့၏ နိုင်ငံရေး ပါတီကို နှစ်သက်မှုအကြောင်း မေးမြန်းပါသည်။ အောက်ပါဇယားသည် စစ်တမ်း၏ရလဒ်များကို ဖော်ပြသည်။

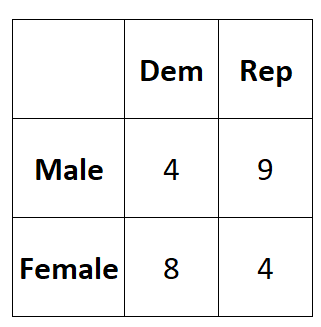
ကိန်းရှင်နှစ်ခုကြားတွင် Phi coefficient ကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0.3589

မှတ်ချက်- Phi coefficient calculator သုံးပြီး ဒါကိုလည်း တွက်ချက်နိုင်ပါတယ်။

Phi coefficient ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

Pearson ဆက်စပ်ကိန်းဂဏန်းနှင့်ဆင်တူသည်၊ Phi coefficient သည် -1 နှင့် 1 ကြားရှိတန်ဖိုးများကို ယူသည်-

• -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်ဆံရေးကို ညွှန်ပြသည်။
• 0 သည် ကိန်းရှင်နှစ်ခုကြားတွင် ဆက်စပ်မှုမရှိကြောင်း ညွှန်ပြသည်။
• 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သော ဆက်ဆံရေးကို ညွှန်ပြသည်။

ယေဘူယျအားဖြင့်၊ နောက်ထပ် Phi coefficient သည် သုညမှဖြစ်ပြီး၊ variable နှစ်ခုကြားရှိ ဆက်နွယ်မှု အားကောင်းလေဖြစ်သည်။

တစ်နည်းဆိုရသော် Phi coefficient သည် သုညမှဖြစ်ပြီး၊ variable နှစ်ခုကြားတွင် စနစ်ကျသော ပုံစံအချို့ရှိကြောင်း အထောက်အထား ပိုများလေဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

Pearson Correlation Coefficient အတွက် လမ်းညွှန်
Fisher Exact Test အတွက် လမ်းညွှန်
Chi-Square Test of Independence အတွက် လမ်းညွှန်