ဖြန့်ဝေပေးလိုက်ပါတယ်။

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ ရှင်းလင်းချက်၊ ၎င်း၏တန်ဖိုးများကို တွက်ချက်ပုံနှင့် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ လက်တွေ့ကမ္ဘာဥပမာကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုကြား ခြားနားချက်များကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။

ဖြန့်ဖြူးရေးလုပ်ဆောင်ချက်ကဘာလဲ။

ဖြန့်ဝေမှု လုပ်ဆောင်ချက်ကို စုစည်းဖြန့်ဝေမှု လုပ်ဆောင်ချက် ဟုလည်း ခေါ်သည် ၊ သည် ဖြန့်ဝေမှုတစ်ခု၏ တိုးပွားဖြစ်နိုင်ခြေကို ညွှန်ပြသည့် သင်္ချာလုပ်ဆောင်ချက်တစ်ခုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ မည်သည့်တန်ဖိုးအတွက်မဆို ဖြန့်ဝေမှုလုပ်ဆောင်ချက်၏ ပုံသည် ကိန်းရှင်သည် ထိုတန်ဖိုး သို့မဟုတ် နိမ့်သောတန်ဖိုးကို ယူသည့်ဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။

၎င်း၏ပုံမှန်သင်္ကေတမှာ မြို့တော် F ဖြစ်သော်လည်း စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို အတိုကောက် FDA မှလည်း ရည်ညွှန်းနိုင်သည်။

ထို့ကြောင့် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်ကို အောက်ပါဖော်မြူလာဖြင့် သတ်မှတ်သည်-

$F(x)=P[X\leq x]$

ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်ကို တွက်ချက်နည်း

ထို့နောက် ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုသည် အဆက်မပြတ် သို့မဟုတ် ဆက်တိုက်ဖြစ်နိုင်မှုအပေါ် မူတည်၍ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ တန်ဖိုးကို မည်သို့တွက်ချက်ရမည်ကို ရှင်းပြပါသည်။

သတိပညာဘောက်စ်

ကျပန်း variable သည် discrete ဖြစ်ပါက၊ စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်သည် x နှင့်ညီမျှသော သို့မဟုတ် နည်းသောတန်ဖိုးများအားလုံး၏ဖြစ်နိုင်ခြေများ၏ပေါင်းလဒ်နှင့်ညီမျှသည်။

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

ရွှေ

$f(u)$

discrete variable နှင့်ဆက်စပ်နေသော ဖြစ်နိုင်ခြေရှိသောလုပ်ဆောင်ချက်ဖြစ်သည်။

ဆက်လုပ်နေတယ်။

ကျပန်း variable သည် စဉ်ဆက်မပြတ်ဖြစ်နေပါက၊ စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်သည် အနှုတ် infinity မှ မေးခွန်းရှိတန်ဖိုးအထိ သိပ်သည်းဆလုပ်ဆောင်မှု၏ ပေါင်းစည်းမှုနှင့် ညီမျှသည်။

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

ရွှေ

$f(u)$

စဉ်ဆက်မပြတ်ကိန်းရှင်နှင့် ဆက်စပ်နေသော သိပ်သည်းဆလုပ်ဆောင်မှုဖြစ်သည်။

ဖြန့်ဝေမှုလုပ်ဆောင်ချက် ဥပမာ

ယခု ကျွန်ုပ်တို့သည် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို သိရှိပြီး၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်တန်ဖိုးကို မည်သို့တွက်ချက်ရမည်ကို လေ့လာရန် လက်တွေ့ကျသော အဆင့်ဆင့်နမူနာကို ကြည့်ကြပါစို့။

အကြွေစေ့ကို လေးကြိမ်လှန်၍ ကျပန်းစမ်းသပ်မှုအတွက် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်ကို တွက်ချက်ပါ။

လေ့ကျင့်ခန်းကိုဖြေရှင်းရန်၊ အကြွေစေ့လေးခေါက်အတွင်းရရှိသော ဦးခေါင်းအရေအတွက်နှင့်ဆက်စပ်နိုင်ခြေအားလုံးကို ဦးစွာတွက်ချက်ရပါမည်။

ထို့ကြောင့်၊ ၎င်းသည် discrete variable ဖြစ်သောကြောင့်၊ distribution function ၏ ပုံများကို ဆုံးဖြတ်ရန်၊ မေးခွန်းရှိ variable ၏တန်ဖိုးအထိ ဖြစ်နိုင်ခြေများကို ပေါင်းထည့်ရန် လုံလောက်ပါသည်။

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

ထို့ကြောင့် လွတ်လပ်သောဒင်္ဂါးပြားလေးခုကို လွှင့်ပစ်ခြင်းဖြင့် ဦးခေါင်းလှန်ခြင်း၏ ဖြန့်ဖြူးရေးလုပ်ဆောင်ချက်၏ တန်ဖိုးများမှာ အောက်ပါအတိုင်းဖြစ်သည်။

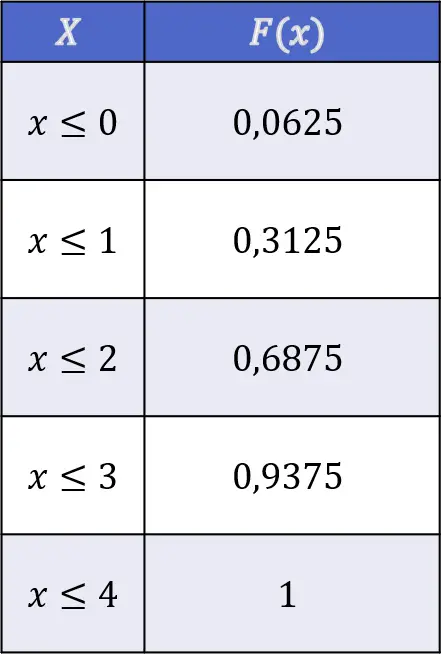
ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ ဂုဏ်သတ္တိများ

ကိန်းရှင်အမျိုးအစား မည်သို့ပင်ရှိစေကာမူ၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်တွင် အောက်ပါဂုဏ်သတ္တိများ အမြဲရှိနေသည်-

စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်၏ တန်ဖိုးသည် 0 နှင့် 1 အကြားတွင် ပါဝင်သည်။

$0\leq F(x) \leq 1$

x သည် infinity သို့ ရွေ့လျားနိုင်သောကြောင့် ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ ကန့်သတ်ချက်သည် 1 နှင့် ညီမျှသည်။

$\displaystyle\lim_{x\to +\infty} F(x)=1$

အခြားတစ်ဖက်တွင်၊ x သည် အနုတ်အနန္တသို့ ချဉ်းကပ်လာသည်နှင့်အမျှ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ ကန့်သတ်ချက်သည် သုညဖြစ်သည်။

$\displaystyle\lim_{x\to -\infty} F(x)=0$

၎င်း၏ဝိသေသလက္ခဏာများအားဖြင့်၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်သည် monotonic ဖြစ်ပြီး လျော့ကျခြင်းမရှိပါ။

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

ထိုမျှသာမကလျှင်
$a\leq b$

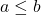
အောက်ပါညီမျှခြင်းများကို ကျေနပ်ပါသည်။

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

ဖြန့်ဝေမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းမှုလုပ်ဆောင်ချက်

နောက်ဆုံးတွင်၊ ဤကိန်းဂဏန်းဆိုင်ရာ အယူအဆနှစ်ခုသည် မကြာခဏ ရှုပ်ထွေးနေသောကြောင့် နောက်ဆုံးတွင်၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုအကြား ကွာခြားချက်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုအကြား ကွာခြားချက် မှာ ၎င်းတို့သတ်မှတ်ထားသော ဖြစ်နိုင်ခြေအမျိုးအစားဖြစ်သည်။ density function သည် variable ၏ အချို့သောတန်ဖိုးတစ်ခုပေါ်တွင် ရရှိသည့်ဖြစ်နိုင်ခြေကို ဖော်ပြသည်၊ ဖြန့်ဖြူးမှု function သည် variable ၏ တိုးပွားဖြစ်နိုင်ခြေကို ဖော်ပြနေချိန်ဖြစ်သည်။

ဆိုလိုသည်မှာ၊ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်ကို ကိန်းရှင်သည် သတ်မှတ်ထားသောတန်ဖိုးထက်နည်းသော ကိန်းရှင်နှင့် ညီမျှသည် သို့မဟုတ် နည်းပါးသည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အသုံးပြုသည်။

သိပ်သည်းမှုလုပ်ဆောင်ချက်သည် စဉ်ဆက်မပြတ်ကိန်းရှင်များကိုသာ ရည်ညွှန်းကြောင်း သတိပြုပါ၊ ထို့ကြောင့် လေ့လာနေသော ကိန်းရှင်သည် စဉ်ဆက်မပြတ်ဖြစ်နေပါက ဤထူးခြားချက်သည် အဓိပ္ပါယ်ရှိမည်ဖြစ်သည်။

ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုသည် ပုံမှန်ဖြန့်ဝေမှု၏ ပျမ်းမျှ 1 နှင့် 0.5 ၏ စံသွေဖည်မှုနောက်ဆက်တွဲဖြစ်သော ကိန်းရှင်၏သိပ်သည်းဆလုပ်ဆောင်ချက်နှင့် နှိုင်းယှဉ်ပါက မည်ကဲ့သို့ပြောင်းလဲသည်ကို သတိပြုပါ။

ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုအကြား ကွာခြားချက်

သိပ်သည်းဆလုပ်ဆောင်မှုအကြောင်း ပိုမိုလေ့လာရန်၊ အောက်ပါဆောင်းပါးကို ကြည့်ပါ။

➤- သိပ်သည်းဆ လုပ်ဆောင်မှုကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။