Root ဆိုသည်မှာ လေးထောင့်ဖြစ်သည်။

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤနေရာတွင် ကျွန်ုပ်တို့သည် မည်သည့် root mean square နှင့် ၎င်းကို မည်ကဲ့သို့ တွက်ချက်သည်ကို ရှင်းပြပါသည်။ ထို့အပြင်၊ ပျမ်းမျှအားအသုံးပြုခြင်း၏ အားသာချက်များနှင့် အားနည်းချက်များကို သင်ယူပြီး အဆင့်ဆင့်ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။ နောက်ဆုံးအနေနဲ့၊ ဆောင်းပါးရဲ့အဆုံးမှာ calculator နဲ့ data set ရဲ့ root mean square ကို တွက်ချက်နိုင်မှာဖြစ်ပါတယ်။

အဓိပ္ပါယ်စတုရန်းဆိုတာဘာလဲ။

အရင်းအနှီးစတုရန်းသည် သရုပ်ဖော်ကိန်းဂဏန်းများ၏ ဗဟိုအချက်အချာကျသော အတိုင်းအတာတစ်ခုဖြစ်သည်။ အရင်းဆိုလို နှစ်ထပ်သည် ဒေတာ၏ နှစ်ထပ်ကိန်းဂဏန်းသင်္ချာပျမ်းမျှ၏ နှစ်ထပ်ကိန်းနှင့် ညီမျှသည်။

Root mean square ကို root mean square သို့မဟုတ် RMS လို့လည်း ခေါ်ပါတယ်။

ထို့ကြောင့် လေးထောင့်ကိန်းအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

ကိန်းဂဏန်းကိန်းရှင်သည် အပြုသဘောနှင့် အနုတ်တန်ဖိုးများကို ယူသောအခါ စတုရန်းဆိုလိုသည် အထူးသဖြင့် အသုံးဝင်သည်၊ အကြောင်းမှာ ဒေတာအပိုင်းအစတစ်ခုစီကို squaring လုပ်ခြင်းဖြင့် တန်ဖိုးများအားလုံးသည် အပြုသဘောဖြစ်လာသည်။ ထို့ကြောင့်၊ နိမိတ်သည် အရေးမကြီးသော်လည်း ၎င်း၏အကြွင်းမဲ့တန်ဖိုးဖြစ်သော ကိန်းရှင်များကို ခွဲခြမ်းစိတ်ဖြာရန် ပျမ်းမျှစတုရန်းကို အသုံးပြုသည်။

ဥပမာအားဖြင့်၊ mean square ကို တိုင်းတာမှုအမှားများကို လေ့လာရန်အသုံးပြုသည်၊ အကြောင်းမှာ ဤကိစ္စများတွင် ကျွန်ုပ်တို့သည် အမှားသည် အပြုသဘောလား သို့မဟုတ် အနုတ်လက္ခဏာကို မကြည့်ဘဲ၊ တိုင်းတာသောအခါတွင် အမှား၏ပြင်းအားကို ပိုင်းခြားစိတ်ဖြာခြင်းသာဖြစ်သည်။

ထို့အပြင် ဂဏန်းကြီးများ၏ လေးထောင့်များသည် သေးငယ်သော ကိန်းဂဏာန်းများထက် တန်ဖိုးများစွာ မြင့်မားသောကြောင့် အလယ်စတုရန်းတွင် ဂဏန်းကြီးများသည် ဂဏန်းငယ်များထက် ပိုအရေးကြီးပါသည်။

Square mean သည် ဂဏန်းသင်္ချာပျမ်းမျှ၊ အလေးချိန်တွက်ဆ၊ ဂျီဩမေတြီပျမ်းမျှနှင့် ဟာမိုနီဆိုလိုတို့နှင့်အတူ ကိန်းဂဏန်းပျမ်းမျှအမျိုးအစားတစ်ခုဖြစ်သည်။

Root Mean Square ၏ အားသာချက်များနှင့် အားနည်းချက်များ

Quadratic ပျမ်းမျှသည် အခြားပျမ်းမျှအမျိုးအစားများနှင့် နှိုင်းယှဉ်ပါက အားသာချက်များနှင့် အားနည်းချက်များရှိသည်။

quadratic mean ၏ အဓိက အားသာချက် မှာ discrete variable ၏ ပျမ်းမျှတန်ဖိုး၏ အလွန်ကောင်းမွန်သော အနီးစပ်ဆုံးကို ရရှိစေခြင်း ဖြစ်သည်။ တစ်ဖက်တွင်၊ စတုရန်းပျှမ်းမျှ၏ ကြီးမားသောအားနည်းချက် မှာ လုပ်ဆောင်ချက်များစွာကို လုပ်ဆောင်ရမည်ဖြစ်သောကြောင့် ၎င်း၏တွက်ချက်မှုမှာ အလွန်ရှုပ်ထွေးပါသည်။

ဆန့်ကျင်ဘက်အားဖြင့်၊ root mean square သည် အမှားတိုင်းတာမှုများကို ပိုင်းခြားစိတ်ဖြာရန် အလွန်အသုံးဝင်သည်။ ဤပိုင်ဆိုင်မှုသည် မှားယွင်းသောတိုင်းတာမှုရလဒ်ကို သိသိသာသာပြောင်းလဲစေမည်ဟု အဓိပ္ပာယ်ဖွင့်ဆိုသော်လည်း၊ ၎င်းသည် မြင့်မားသောတန်ဖိုးများအတွက်လည်း ပို၍အရေးကြီးပါသည်။

root mean square ကို ဘယ်လိုတွက်ရမလဲ

root mean square ကို တွက်ချက်ရန်၊ အောက်ပါ အဆင့်များကို လုပ်ဆောင်ရပါမည်။

ကိန်းဂဏန်းအချက်အလက်တစ်ခုစီ၏ နှစ်ထပ်ကိန်းကို တွက်ချက်ပါ။
ယခင်အဆင့်တွင် တွက်ချက်ထားသော လေးထောင့်အားလုံးကို ပေါင်းထည့်ပါ။
နမူနာရှိ ဒေတာပစ္စည်း အရေအတွက်ဖြင့် ရလဒ်ကို ပိုင်းခြားပါ။
ယခင်တန်ဖိုး၏ နှစ်ထပ်ကိန်းကို ရှာပါ။
ရရှိသောရလဒ်သည် ကိန်းဂဏန်းနမူနာ၏ စတုရန်းပျမ်းမျှဖြစ်သည်။

👉 မည်သည့်ဒေတာအစုံ၏ root mean square ကိုတွက်ရန် အောက်ပါ calculator ကိုသုံးနိုင်သည်။

အဓိပ္ပါယ် စတုရန်းပုံဥပမာ

root mean square ကို ဘယ်လိုလုပ်ရမယ်ဆိုတာ သိပြီးတာနဲ့ ဥပမာတစ်ခုအနေနဲ့ data set တစ်ခုရဲ့ root mean square ကို ဆုံးဖြတ်ပါမယ်။

တက္ကသိုလ်ဓာတ်ခွဲခန်းတစ်ခုတွင် ပါမောက္ခက ကျောင်းသားများအား ဓာတုဗေဒပစ္စည်းဖြင့် စမ်းသပ်မှုပြုလုပ်ရန် တောင်းဆိုသည်။ ဓာတုစမ်းသပ်မှု၏ ရည်ရွယ်ချက်မှာ စုစုပေါင်း 3 လီတာ၏ အဖြေကို ရရှိရန်ဖြစ်သည်။ ကျောင်းသားအဖွဲ့များသည် အောက်ပါအချက်အလက်များကို ရရှိခဲ့ပါသည်။

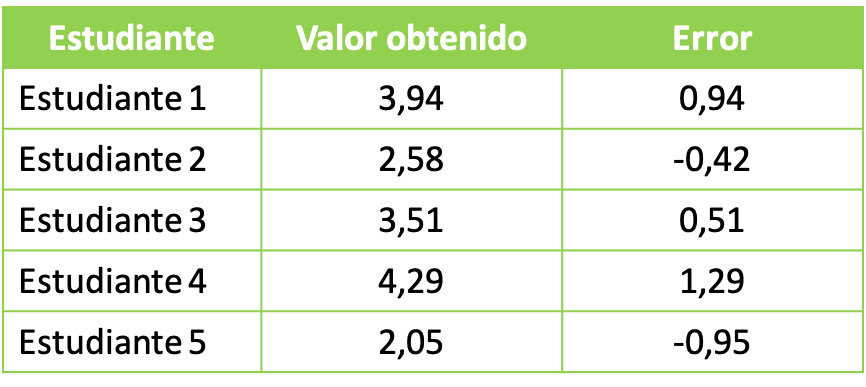
ရရှိသော ကိန်းဂဏန်းအချက်အလက်များကို လေ့လာရန်အတွက် အုပ်စုတစ်ခုစီမှရရှိသော အမှားဖြင့် စတုရန်းပျမ်းမျှတန်ဖိုးကို တွက်ချက်ရန် ဆက်လက်လုပ်ဆောင်ပါသည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် လေးထောင့်ပုံသဏ္ဍာန်ကို အသုံးပြုသည်။

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

ပြီးတော့ ဒေတာကို ဖော်မြူလာနဲ့ အစားထိုးပြီး root mean square ကို တွက်ချက်ပါတယ်။

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

ထို့ကြောင့်၊ စမ်းသပ်မှုတွင်ရရှိသော ပျမ်းမျှအမှားသည် 0.88 လီတာဖြစ်သည်။

Mean Square Calculator

၎င်း၏ root mean square ကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ထဲသို့ မည်သည့် ကိန်းဂဏန်းနမူနာမှ ဒေတာကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။