Poisson ဖြန့်ဖြူးမှုအတွက် mle (တစ်ဆင့်ပြီးတစ်ဆင့်)
အများဆုံးဖြစ်နိုင်ခြေ ခန့်မှန်းချက် (MLE) သည် ပေးထားသော ဖြန့်ဖြူးမှု၏ ဘောင်များကို ခန့်မှန်းရန် အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။
Poisson ဖြန့်ချီမှု ၏ parameter λ အတွက် MLE ကို တွက်ချက်နည်း ဤသင်ခန်းစာတွင် ရှင်းပြထားသည်။
အဆင့် 1: PDF ကိုရေးပါ။
ပထမဦးစွာ Poisson ဖြန့်ဖြူးမှု၏ ဖြစ်နိုင်ခြေသိပ်သည်းဆလုပ်ဆောင်ချက်ကို ရေးပါ။
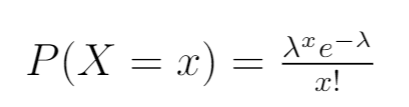
အဆင့် 2- ဖြစ်နိုင်ခြေရှိသောလုပ်ဆောင်ချက်ကိုရေးပါ။
ထို့နောက် ဖြစ်နိုင်ချေရှိသော လုပ်ဆောင်ချက်ကို ရေးပါ။ ဤသည်မှာ သတိပြုမိသော တန်ဖိုးများ x 1 , …, x n အတွက် PDF ၏ ထုတ်ကုန်ဖြစ်သည်။
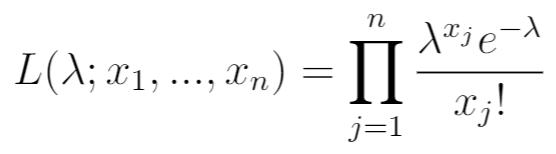
အဆင့် 3- သဘာဝ လော့ဂရစ်သမ်၏ ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်ကို ရေးပါ။
တွက်ချက်မှုများကို ရိုးရှင်းစေရန်၊ ကျွန်ုပ်တို့သည် သဘာဝဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်ကို ရေးသားနိုင်သည်-
အဆင့် 4- λ နှင့်စပ်လျဉ်း၍ သဘာဝဖြစ်နိုင်ခြေလုပ်ဆောင်မှု၏ ဆင်းသက်လာမှုကို တွက်ချက်ပါ။
ထို့နောက် ကျွန်ုပ်တို့သည် parameter λ နှင့်စပ်လျဉ်း၍ သဘာဝဖြစ်နိုင်ခြေလုပ်ဆောင်မှု၏ ဆင်းသက်လာမှုကို တွက်ချက်နိုင်သည်။
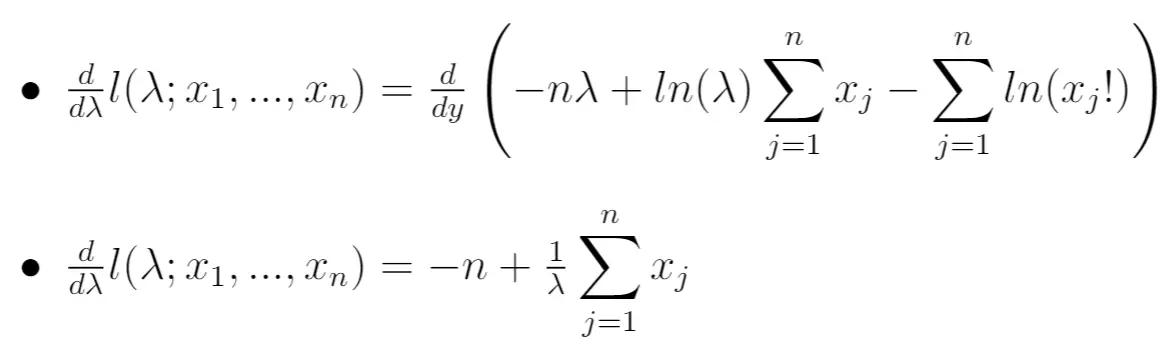
အဆင့် 5- ဆင်းသက်ခြင်းကို သုညနှင့်ညီအောင်သတ်မှတ်ပြီး λ ကိုဖြေရှင်းပါ။
နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ယခင်အဆင့်မှ သုညနှင့်ညီသော ဆင်းသက်လာမှုကို သတ်မှတ်ပြီး λ အတွက် ဖြေရှင်းလိုက်ပါသည်။
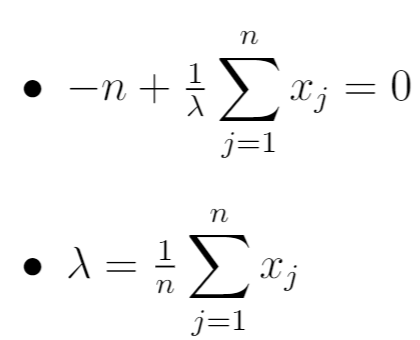
ထို့ကြောင့် MLE သည်-
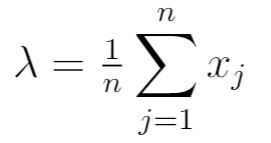
၎င်းသည် နမူနာရှိ n လေ့လာမှုများ၏ နမူနာပျမ်းမျှ နှင့် ညီမျှသည်။
ထပ်လောင်းအရင်းအမြစ်များ
Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်
ငါးဖြန့်ဝေဂဏန်းတွက်စက်
Excel တွင် Poisson distribution ကိုအသုံးပြုနည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။