စာရိုက်သည်။
ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် ဖြန့်ဖြူးမှုတစ်ခုအား ဖော်ပြခြင်း၏အဓိပ္ပါယ်ကို ရှင်းပြထားသည်။ ထို့ကြောင့် သင်သည် စာစီစာရိုက်ခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ကိန်းရှင်တစ်ခု၏ စာစီစာရိုက်ခြင်း၏ ဥပမာတစ်ခုနှင့် ထို့အပြင်၊ တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုဖြင့် လေ့ကျင့်နိုင်မည်ဖြစ်သည်။
စာရိုက်ခြင်းဆိုတာဘာလဲ။
စာရင်းဇယားများတွင်၊ ပုံမှန်ပြုလုပ်ခြင်း ဆိုသည်မှာ ၎င်း၏ပျမ်းမျှနှင့် စံသွေဖည်မှုဖြစ်သည့် သုညနှင့် တစ်ခု အသီးသီးရှိသော ဖြန့်ဖြူးမှုတစ်ခုသို့ မျဉ်းကြောင်းပြောင်းခြင်းကို အသုံးချသည့် လုပ်ငန်းစဉ်တစ်ခုဖြစ်သည်။
ပိုမိုတိကျစွာ၊ စာရိုက်ခြင်းတွင် ကျပန်းကိန်းရှင်မှ ပျမ်းမျှကို နုတ်ပြီး စံသွေဖည်မှုဖြင့် ပိုင်းခြားခြင်း ပါဝင်ပါသည်။
စာရိုက်ခြင်းကို normalization သို့မဟုတ် standardization ဟုခေါ်သည်။
ထည့်သွင်းဖော်မြူလာ
ကိန်းရှင်တစ်ခုကို အမျိုးအစားခွဲရန်၊ ၎င်းကို ၎င်း၏ ပျမ်းမျှသွေဖည်မှုဖြင့် ပိုင်းခြားရပါမည်။ ထို့ကြောင့် ကိန်းရှင်တစ်ခုကို ထည့်သွင်းခြင်းအတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။
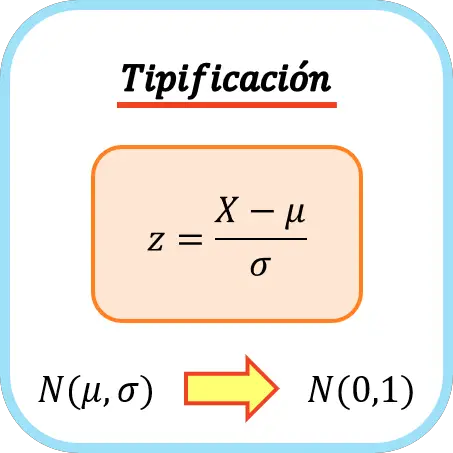
ရွှေ
![]()
variable ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
![]()
နှင့်
![]()
၎င်း၏ စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု)။
ထို့ကြောင့်၊ entry သည် variable တွင် linear transformation ကိုအသုံးပြုထားသောကြောင့်၊ entry သည် variable change တစ်ခုဖြစ်သည်။
နမူနာ ဝင်ခွင့်
စာစီစာကုံး၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် သဘောတရားကို အပြည့်အဝနားလည်ရန် အောက်တွင် ခိုင်မာသော ဥပမာတစ်ခုဖြစ်သည်။
- စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်တစ်ခုသည် ပျမ်းမျှ 45 နှင့် စံသွေဖည်မှု 10 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်ပြီး၊ 60 ထက်နည်းသော သို့မဟုတ် ညီမျှသည့်တန်ဖိုးကိုရရှိရန် ဖြစ်နိုင်ခြေမှာ အဘယ်နည်း။
![]()
ပုံမှန်ဖြန့်ဖြူးမှု၏ဖြစ်နိုင်ခြေကိုရှာဖွေရန် ၎င်း၏လက္ခဏာဇယားကိုအသုံးပြုရန် လိုအပ်သော်လည်း ၎င်းကိုပြုလုပ်ရန် စာရိုက်ခြင်းလုပ်ငန်းစဉ်ကို ဦးစွာလုပ်ဆောင်ရန် လိုအပ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ပျမ်းမျှကို နုတ်ပြီး ဖြစ်နိုင်ခြေတန်ဖိုးသို့ စံသွေဖည်မှုဖြင့် ပိုင်းခြားသည်-
![]()
ကျွန်ုပ်တို့ စံသတ်မှတ်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် 1.5 ၏ တန်ဖိုးနှင့် ဆက်စပ်နိုင်ခြေကို ကြည့်ရန် ပုံမှန် ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေ ဇယားသို့ ဆက်သွားရန်။

သာမာန်ဖြန့်ဝေမှု စာစီစာကုံးဇယားတွင် တွေ့မြင်နိုင်သကဲ့သို့၊ ယခင်အဆင့်တွင် တွက်ချက်ထားသော တန်ဖိုးသည် အောက်ပါဖြစ်နိုင်ခြေနှင့် ကိုက်ညီသည်-
![]()
ထို့ကြောင့် 60 နှင့် ညီမျှသော သို့မဟုတ် ထက်နည်းသော တန်ဖိုးတစ်ခုရရှိရန် ဖြစ်နိုင်ခြေသည် 93.32% ဖြစ်သည်။
စာရိုက်လေ့ကျင့်မှု ဖြေရှင်းပြီးသား
ပျမ်းမျှနှင့် စံသွေဖည်မှု 120 နှင့် 50 အသီးသီးရှိသော ပုံမှန်ဖြန့်ဖြူးမှု၏ အောက်ပါဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။
![]()
- 208 ထက်နည်းသော သို့မဟုတ် ညီမျှသောတန်ဖိုးကိုရရှိရန်ဖြစ်နိုင်ခြေ။
- 137 ထက်ကြီးသောတန်ဖိုးကိုရရှိရန်ဖြစ်နိုင်ခြေ။
ပြဿနာ၏ ကဏ္ဍနှစ်ခုစလုံးတွင် ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် ပုံမှန်ဖြန့်ဖြူးမှုတွင် ရိုက်ထည့်ရန် လိုအပ်သည်။
ကျွန်ုပ်တို့သည် 208 ထက်နည်းသော သို့မဟုတ် ညီမျှသော တန်ဖိုးတစ်ခု၏ ဖြစ်နိုင်ခြေကို ရိုက်နှိပ်ခြင်းဖြင့် တွက်ချက်ခြင်းဖြင့် စတင်သည်-
![]()
ယခုတွင်၊ တန်ဖိုး 1.76 သည် မည်သည့်ဖြစ်နိုင်ခြေနှင့် သက်ဆိုင်သည်ကို အထက်ဇယားတွင် ကြည့်ကြပါစို့။
![]()
ဒုတိယအနေဖြင့်၊ ကျွန်ုပ်တို့သည် 137 ထက်ကြီးသောတန်ဖိုးကိုရရှိရန်ဖြစ်နိုင်ခြေကိုတွက်ချက်ပါမည်။ ထိုနည်းအတိုင်းပင်၊ ကိန်းရှင်ကိုရိုက်ခြင်းဖြင့်စတင်သည်-
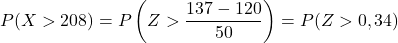 သို့သော်၊ ပူးတွဲပါဇယားတွင် အနိမ့်ဆုံးဖြစ်နိုင်ခြေများသာ ရှိသည်၊ ထို့ကြောင့် ဇယားကိုအသုံးပြုရန်အတွက် ဖြစ်နိုင်ခြေကို ဦးစွာပြောင်းလဲရပါမည်-
သို့သော်၊ ပူးတွဲပါဇယားတွင် အနိမ့်ဆုံးဖြစ်နိုင်ခြေများသာ ရှိသည်၊ ထို့ကြောင့် ဇယားကိုအသုံးပြုရန်အတွက် ဖြစ်နိုင်ခြေကို ဦးစွာပြောင်းလဲရပါမည်-
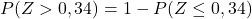 နောက်ဆုံးတွင်၊ ပူးတွဲဇယားမှ Z ၏တွက်ချက်မှုတန်ဖိုးနှင့် သက်ဆိုင်သောဖြစ်နိုင်ခြေကို မှတ်သားပါမည်-
နောက်ဆုံးတွင်၊ ပူးတွဲဇယားမှ Z ၏တွက်ချက်မှုတန်ဖိုးနှင့် သက်ဆိုင်သောဖြစ်နိုင်ခြေကို မှတ်သားပါမည်-
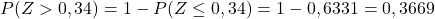
စာရိုက်ရန်အချက်ကဘာလဲ။
စာစီစာရိုက်ခြင်း၏ အဓိပ္ပါယ်ကို နားလည်ရန် အပြီးသတ်ရန်၊ ၎င်းကို မည်သည့်အတွက် အသုံးပြုကြောင်းနှင့် ကိန်းရှင်တစ်ခုကို ရိုက်ထည့်ရမည့်အချိန်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။
အဓိကအားဖြင့်၊ ဖြန့်ဖြူးမှုတန်ဖိုးများကို မတူညီသောနည်းလမ်းများနှင့် ကွဲပြားမှုများဖြင့် နှိုင်းယှဉ်ရန် စံသတ်မှတ်ခြင်းကို အသုံးပြုပါသည်။ အလားတူဖြစ်နိုင်ခြေကို တွက်ချက်ရန် စံသတ်မှတ်ခြင်းကိုလည်း အသုံးပြုပါသည်။
မတူညီသောဝိသေသလက္ခဏာများဖြင့် ဖြန့်ဖြူးမှုတန်ဖိုးနှစ်ခုကို စံသတ်မှတ်ခြင်းဖြင့်၊ မည်သည့်တန်ဖိုးသည် ဖြန့်ဖြူးမှုတစ်ခုလုံးနှင့် နှိုင်းယှဉ်လျှင် ပိုကြီးသည် သို့မဟုတ် သေးငယ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ သို့မဟုတ် တစ်နည်းအားဖြင့် စာစီစာရိုက်ခြင်းလုပ်ငန်းစဉ်ကို ကျင့်သုံးခြင်းဖြင့်၊ မည်သည့်တန်ဖိုးသည် ၎င်း၏ ဖြန့်ဖြူးမှု၏ ဆိုလိုရင်းမှ အနီးစပ်ဆုံး သို့မဟုတ် အဝေးဆုံးဖြစ်သည်ကို ကျွန်ုပ်တို့ မြင်တွေ့နိုင်သည်။
ထို့အပြင်၊ အထက်တွင်ရှင်းပြထားသည့်အတိုင်း၊ စာစီစာရိုက်သည် ဖြစ်နိုင်ချေများကို တွက်ချက်ရာတွင်လည်း ခွင့်ပြုပေးသည်၊ အဘယ်ကြောင့်ဆိုသော် ယေဘုယျအားဖြင့် ဖြစ်နိုင်ခြေဇယားများသည် စာစီစာကုံးဖြန့်ဝေမှုအပေါ် အခြေခံထားသောကြောင့် ဖြစ်နိုင်ခြေများသည်။