ယူနီဖောင်းဖြန့်ဝေခြင်းမိတ်ဆက်

တူညီသောဖြန့်ဝေမှုသည် a မှ b ကြားကာလတစ်ခုကြားရှိတန်ဖိုးတစ်ခုစီတွင်ဖြစ်ပေါ်နိုင်ခြေတူညီသောဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

ကျပန်း ကိန်းရှင် X သည် တစ်ပြေးညီ ဖြန့်ဝေမှုနောက်တွင် လိုက်နေပါက၊ X သည် x ₁ နှင့် x ₂ ကြား တန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

ရွှေ-

• x ₁ : အတိုးနှုန်းနိမ့်
• x ₂ : အတိုး၏အထက်တန်ဖိုး
• a- ဖြစ်နိုင်ချေ အနည်းဆုံးတန်ဖိုး
• b- ဖြစ်နိုင်ချေ အများဆုံးတန်ဖိုး

ဥပမာအားဖြင့်၊ လင်းပိုင်၏အလေးချိန်သည် ပေါင် 100 နှင့် 150 အကြားအညီအမျှခွဲဝေနေသည်ဆိုပါစို့။

အကယ်၍ ကျွန်ုပ်တို့သည် လင်းပိုင်ကို ကျပန်းရွေးချယ်ပါက၊ ရွေးချယ်ထားသော လင်းပိုင်သည် ပေါင် 120 မှ 130 ကြား အလေးချိန်ရှိနိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

• P(120 < X < 130 ) = ( 130 – 120 ) / ( 150 – 100 )
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0.2

ရွေးချယ်ထားသော လင်းပိုင်သည် ပေါင် 120 နှင့် 130 အကြားအလေးချိန်ရှိနိုင်ခြေမှာ 0.2 ဖြစ်သည်။

ယူနီဖောင်း ဖြန့်ဖြူးမှုကို မြင်ယောင်ကြည့်ပါ။

ယူနီဖောင်းဖြန့်ဖြူးမှုကို မြင်သာစေရန် သိပ်သည်းဆကွက်ကွက်တစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် အောက်ပါကွက်ကွက်နှင့် တူလိမ့်မည်-

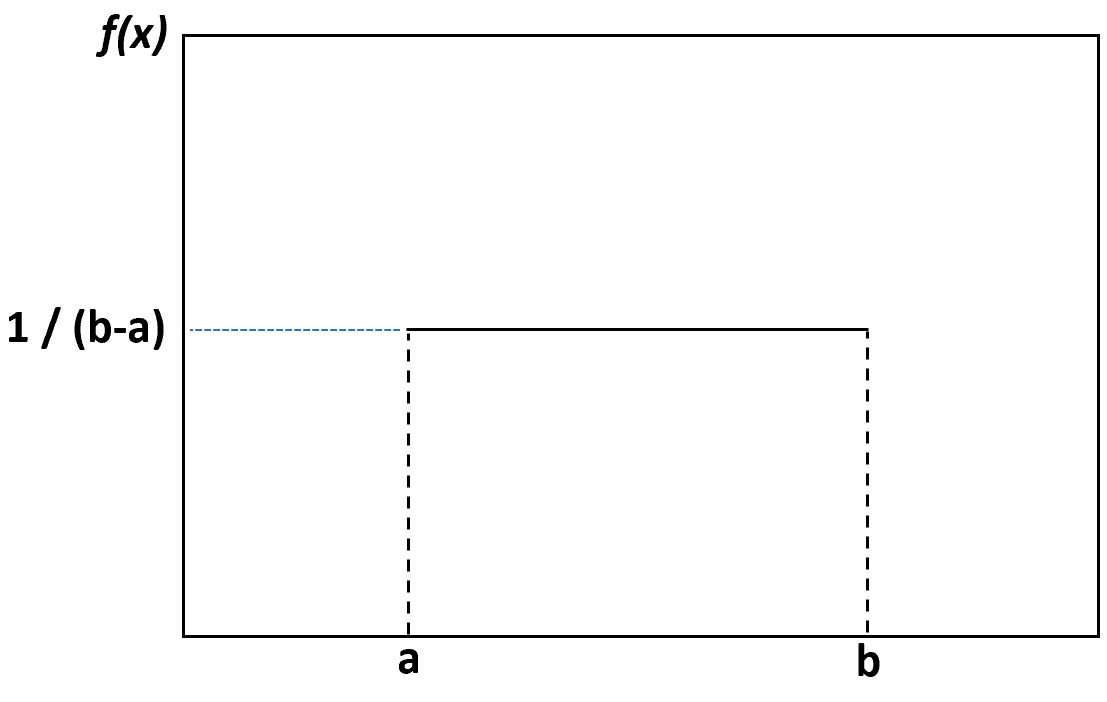
အောက်ကန့်သတ်ချက် a နှင့် အထက်ကန့်သတ်ချက် b ကြားရှိ တန်ဖိုးတိုင်းတွင် တူညီသောဖြစ်နိုင်ခြေများရှိပြီး အဆိုပါကန့်သတ်ချက်များအပြင်ရှိ မည်သည့်တန်ဖိုးမဆို ဖြစ်နိုင်ခြေမှာ သုညဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ယခင်နမူနာတွင်၊ လင်းပိုင်များ၏အလေးချိန်သည် ပေါင် ၁၀၀ မှ ၁၅၀ ကြား အညီအမျှ ခွဲဝေသည်ဟု ဆိုပါသည်။ ဤဖြန့်ဝေပုံကို မြင်ယောင်ပုံမှာ ဤအရာဖြစ်သည်-

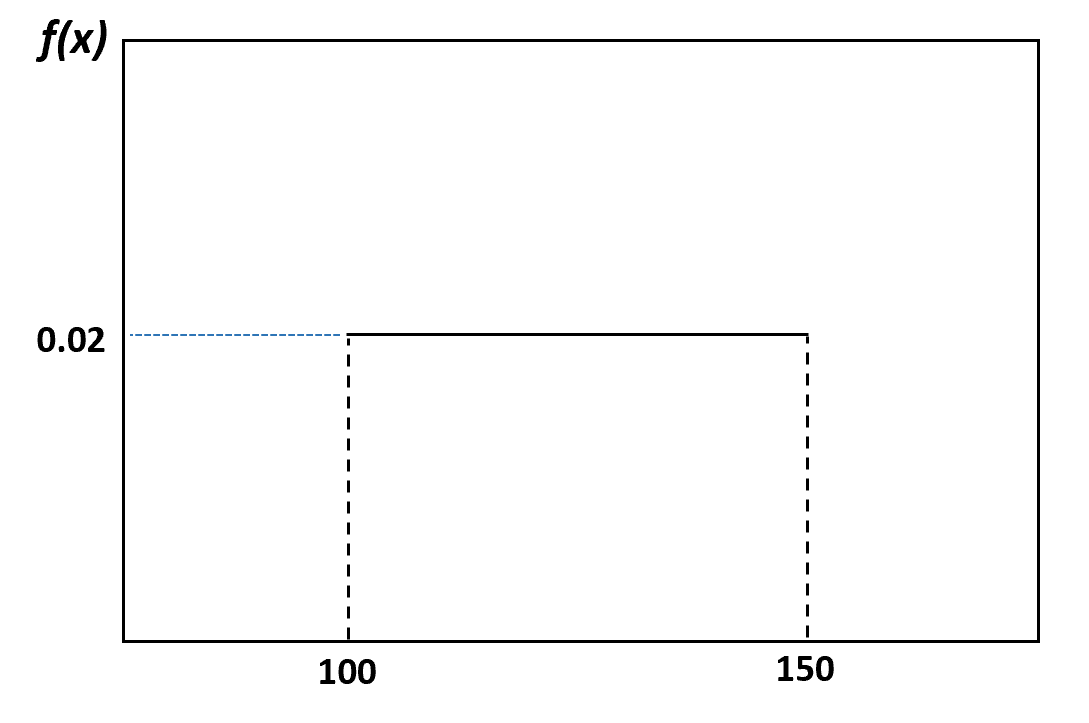
ကျပန်းရွေးချယ်ထားသော လင်းပိုင်သည် ပေါင် 120 နှင့် 130 အကြားအလေးချိန်ရှိသော ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း မြင်နိုင်သည်။

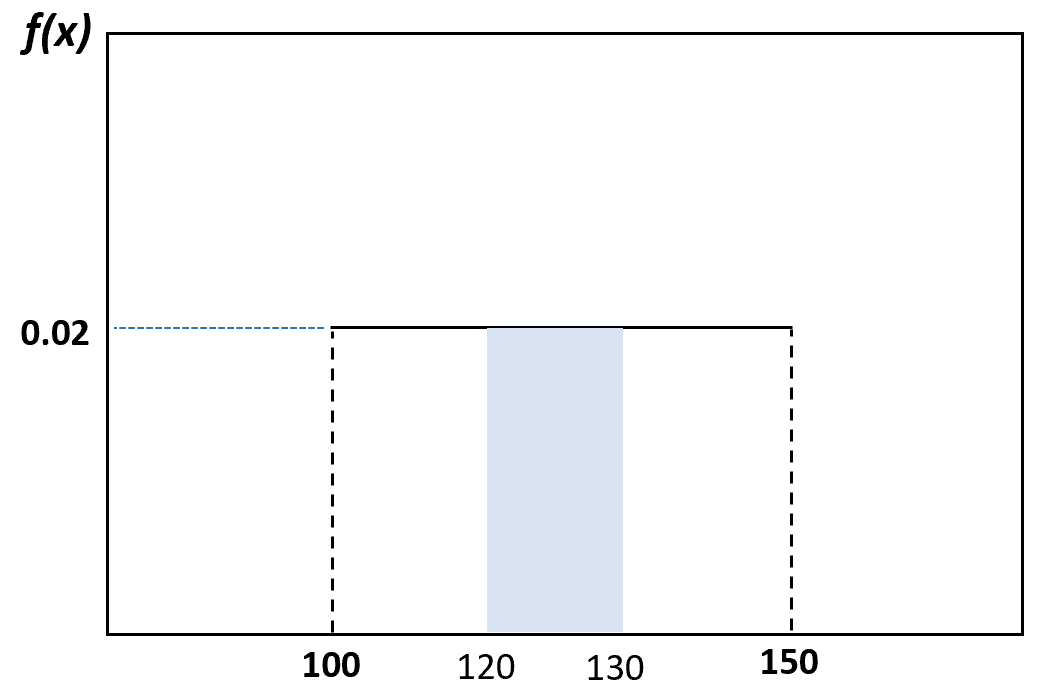
တစ်ပြေးညီ ဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများ

ယူနီဖောင်း ဖြန့်ဖြူးမှုတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

• ပျမ်းမျှ: (a + b) / 2
• မီဒီယံ: (က+ခ)/၂
• စံသွေဖည်မှု- √ (ခ – a) ^2/12
• ကွာခြားချက်- (ခ – က) ^၂/၁၂

ဥပမာအားဖြင့်၊ လင်းပိုင်၏အလေးချိန်သည် ပေါင် 100 နှင့် 150 အကြားအညီအမျှခွဲဝေနေသည်ဆိုပါစို့။

ဤဖြန့်ဖြူးမှုအတွက် အောက်ပါဂုဏ်သတ္တိများကို ကျွန်ုပ်တို့ တွက်ချက်နိုင်သည်-

• ပျမ်းမျှအလေးချိန်- (a + b) / 2 = (150 + 100) / 2 = 125
• ပျမ်းမျှအလေးချိန်- (a + b) / 2 = (150 + 100) / 2 = 125
• အလေးချိန်၏စံသွေဖည်မှု- √ (150 – 100) ^2/12 = 14.43
• အလေးချိန်ကွဲလွဲမှု- (150 – 100) ^2/12 = 208.33

Uniform Distribution Practices ဆိုင်ရာ ပြဿနာများ

ယူနီဖောင်းဖြန့်ဖြူးခြင်းဆိုင်ရာ သင်၏အသိပညာကို စမ်းသပ်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။

မေးခွန်း 1- ဘတ်စ်ကားတစ်စီးသည် မိနစ် 20 တိုင်း ဘတ်စ်ကားမှတ်တိုင်သို့ ရောက်သည်။ ဘတ်စ်ကားမှတ်တိုင်ကိုရောက်ရင် 8 မိနစ်အတွင်း ဘတ်စ်ကားရောက်လာဖို့ ဖြစ်နိုင်ခြေ ဘယ်လောက်ရှိလဲ။

ဖြေရှင်းချက် 1- အနည်းဆုံးစောင့်ဆိုင်းချိန်သည် 0 မိနစ်ဖြစ်ပြီး အမြင့်ဆုံးစောင့်ဆိုင်းချိန်မှာ မိနစ် 20 ဖြစ်သည်။ အောက်အတိုးတန်ဖိုးသည် 0 မိနစ်ဖြစ်ပြီး အထက်အတိုးတန်ဖိုးမှာ 8 မိနစ်ဖြစ်သည်။

ဒါကြောင့် ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါမယ်။

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 ။

မေးခွန်း 2- NBA ဂိမ်းတစ်ခု၏ကြာချိန်သည် မိနစ် 120 နှင့် 170 ကြားတွင် အညီအမျှ ဖြန့်ဝေပါသည်။ ကျပန်းရွေးချယ်ထားသော NBA ဂိမ်းသည် 155 မိနစ်ထက် ပိုကြာနိုင်ခြေ မည်မျှရှိသနည်း။

ဖြေရှင်းချက် 2- အနည်းဆုံးကြာချိန်သည် မိနစ် 120 ဖြစ်ပြီး အမြင့်ဆုံးကြာချိန်မှာ 170 မိနစ်ဖြစ်သည်။ အောက်အတိုးတန်ဖိုးသည် ၁၅၅ မိနစ်ဖြစ်ပြီး အထက်အတိုးတန်ဖိုးမှာ မိနစ် ၁၇၀ ဖြစ်သည်။

ဒါကြောင့် ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါမယ်။

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 ။

မေးခွန်း 3- အချို့ဖားမျိုးစိတ်များ၏ အလေးချိန်သည် 15 မှ 25 ဂရမ်ကြား အညီအမျှခွဲဝေပါသည်။ ဖားတစ်ကောင်ကို ကြုံသလိုရွေးရင် အလေးချိန် 17 ဂရမ်ကနေ 19 ဂရမ်ကြား ဖြစ်နိုင်ခြေဘယ်လောက်ရှိလဲ။

ဖြေရှင်းချက် 3- အနိမ့်ဆုံးအလေးချိန်မှာ 15 ဂရမ်ဖြစ်ပြီး အမြင့်ဆုံးအလေးချိန်မှာ 25 ဂရမ်ဖြစ်သည်။ အောက်အတိုးတန်ဖိုးသည် ၁၇ ဂရမ်ဖြစ်ပြီး အထက်အတိုးတန်ဖိုးမှာ ၁၉ ဂရမ်ဖြစ်သည်။

ဒါကြောင့် ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါမယ်။

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 ။

မှတ်ချက်- ဤပြဿနာတစ်ခုစီအတွက် ကျွန်ုပ်တို့၏အဖြေများကို စစ်ဆေးရန် Uniform Distribution Calculator ကို အသုံးပြုနိုင်ပါသည်။