စုဆောင်းထားသော ပကတိအကြိမ်ရေ

ဤဆောင်းပါးတွင် စုဆောင်းထားသော absolute frequency သည် မည်သည့်အရာနှင့် ၎င်းကိုအသုံးပြုသည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ဒေတာအစုတစ်ခုမှ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို မည်သို့ရယူရမည်၊ ထို့အပြင်၊ လေ့ကျင့်ခန်း နှစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းနိုင်သည်ကို တွေ့ရမည်ဖြစ်ပါသည်။

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းဆိုတာ ဘာလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း သည် အကြွင်းမဲ့ ကြိမ်နှုန်းများ၏ စုစည်းမှုပေါင်းစုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ တန်ဖိုးတစ်ခု၏ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းသည် ထိုတန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် ၎င်းထက်နည်းသော တန်ဖိုးအားလုံး၏ ပကတိကြိမ်နှုန်းများနှင့် ညီမျှသည်။

ပုံမှန်အားဖြင့်၊ စာရင်းဇယားများတွင်၊ subscript i ပါသော စာလုံးကြီး F ကို တန်ဖိုး i ၏ တိုးပွားလာသော ပကတိအကြွင်းမဲ့ကြိမ်နှုန်းကို ကိုယ်စားပြုရန်အတွက် အသုံးပြုသည်၊ ထို့ကြောင့် တိုးပွားလာသော absolute frequency အတွက် သင်္ကေတမှာ F _i ဖြစ်သည်။

ယုတ္တိဗေဒအရ၊ စုဆောင်းထားသော absolute frequency ဆိုသည်မှာ အဘယ်အရာကို နားလည်ရန်၊ absolute frequency သဘောတရားကို ရှင်းရှင်းလင်းလင်း သိထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ရှင်းလင်းချက်မတင်မီ အောက်ပါဆောင်းပါးကို စစ်ဆေးရန် အကြံပြုအပ်ပါသည်။

စုစည်းမှု အကြွင်းမဲ့ အကြိမ်ရေ တွက်နည်း

တိုးပွားလာသော absolute frequency ကို တွက်ချက်ရန် အဆင့်များမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

1. ဒေတာအတွဲတွင် ပေါ်လာသည့် မတူညီသောတန်ဖိုးများအားလုံးကို ဇယားတစ်ခုဖန်တီးပါ၊ ဆိုလိုသည်မှာ ဇယားတစ်ခု၏အတန်းတစ်ခုစီတွင် မတူညီသောတန်ဖိုးတစ်ခုစီကို နေရာချပါ။
2. တန်ဖိုးတစ်ခုစီ၏ ပကတိအကြိမ်ရေကို ဆုံးဖြတ်သည်။
3. တန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်ထားသည့် တန်ဖိုးတစ်ခုစီ၏ ပကတိအကြွင်းမဲ့ ကြိမ်နှုန်းကို ရှာပါ။

ကိန်းရှင်သည် စဉ်ဆက်မပြတ်ဖြစ်နေပါက သို့မဟုတ် ကွဲပြားသောတန်ဖိုးများစွာရှိနေပါက၊ သင်သည် ဒေတာကို ပထမဦးစွာ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ပြီး တိုးပွားလာသော absolute frequency ကိုရှာဖွေရန် အထက်ဖော်ပြပါအဆင့်များကို ကျင့်သုံးရန် သတိရပါ။

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း ဥပမာများ

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်မြင်နိုင်စေရန်၊ အောက်တွင် လက်တွေ့ကမ္ဘာ ဥပမာနှစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖော်ပြပါသည်။ ပထမဥပမာတွင်၊ discrete variable ၏ တိုးမြင့်လာသော absolute frequencies နှင့် ဒုတိယအဆင့်တွင် စဉ်ဆက်မပြတ် variable ၏ တွက်ချက်မှုကို ခံရသည်။

ဥပမာ 1- အဆက်မပြတ်ပြောင်းလဲနိုင်သော

• အတန်းတစ်တန်းတွင် ကျောင်းသား အယောက် ၃၀ ၏ စာရင်းဇယားတွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်း ဖြစ်သည်။ မှတ်စုတစ်ခုစီ၏ ပကတိအကြွင်းမဲ့ ကြိမ်နှုန်းသည် အဘယ်နည်း။

ဂဏန်းများအားလုံးသည် ကိန်းပြည့်များသာဖြစ်နိုင်သောကြောင့် ၎င်းသည် သီးခြားကွဲလွဲချက်ဖြစ်သည်။ ထို့ကြောင့် အချက်အလက်များကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ရန် မလိုအပ်ပါ။

ထို့ကြောင့်၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို ဆုံးဖြတ်ရန်၊ ကိန်းဂဏန်းနမူနာတွင် တန်ဖိုးတစ်ခုစီတွင် ပေါ်လာသည့် အကြိမ်အရေအတွက်ဖြစ်သည့် တန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ဦးစွာရှာဖွေရပါမည်။

ယခု ကျွန်ုပ်တို့သည် absolute frequency ကို သိရှိပြီး၊ စုစည်းမှု absolute frequency ကို တွက်ချက်နိုင်ပါပြီ။ ၎င်းကိုလုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်- ကျွန်ုပ်တို့သည် တန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် အသေးငယ်ဆုံးတန်ဖိုးများ၏ ပကတိကြိမ်နှုန်းအားလုံးကို ပေါင်းထည့်ခြင်း သို့မဟုတ် ဆန့်ကျင်ဘက်အနေနှင့်၊ ကျွန်ုပ်တို့သည် တန်ဖိုး၏ absolute frequency နှင့် ယခင်တန်ဖိုးများ၏ ပကတိအကြိမ်ရေကို ပေါင်းထည့်သည် . တန်ဖိုး။

အတိုချုပ်အားဖြင့်၊ လေ့ကျင့်ခန်း၏ ပကတိ တိုးပွားလာသော အကြိမ်ရေနှင့် ဇယားမှာ အောက်ပါအတိုင်း ဖြစ်သည်။

နောက်ဆုံးတန်ဖိုး၏ စုစည်းမှု ပကတိအကြိမ်ရေသည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် အမြဲသက်ဆိုင်ကြောင်း သတိပြုပါ။ မဟုတ်ပါက သင်သည် တွက်ချက်မှုတွင် မှားယွင်းသွားသည်ဟု ဆိုလိုသည်။

ဥပမာ 2- စဉ်ဆက်မပြတ်ကိန်းရှင်

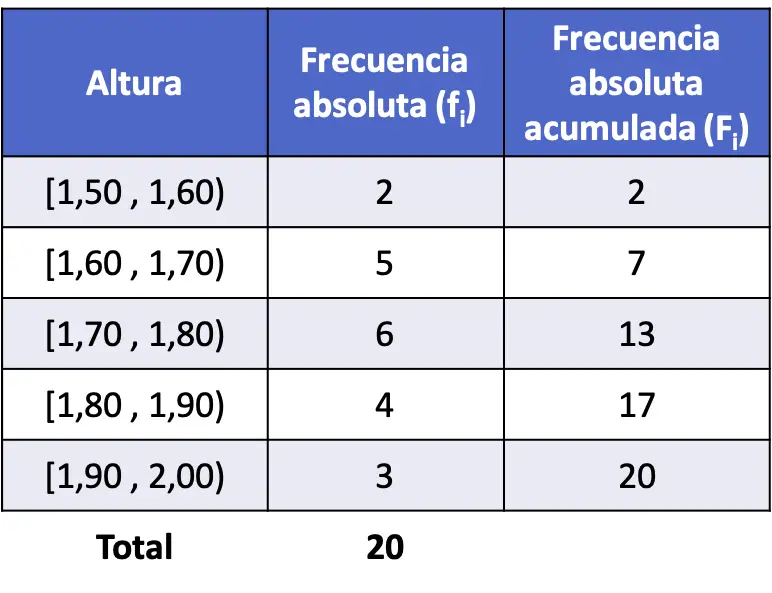
• လူ 20 ၏ အရပ်အမြင့်ကို တိုင်းတာခဲ့ပြီး အောက်ဖော်ပြပါ ရလဒ်များကို ရရှိခဲ့သည်။ ဒေတာကို ကြားကာလများအဖြစ် ပိုင်းခြားပြီး ကြားကာလတစ်ခုစီအတွက် စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို တွက်ချက်သည်။

ဤဥပမာရှိ ဖြန့်ဝေမှုသည် စဉ်ဆက်မပြတ်ဖြစ်သည်၊ ဒဿမ ဂဏန်းများ ရှိနိုင်သောကြောင့် ဒေတာကို မတူညီသော ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ခြင်းသည် အကောင်းဆုံးဖြစ်သည်။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဒေတာကို ကြားကာလများအဖြစ် ပိုင်းခြားပြီး အကြွင်းမဲ့ အကြိမ်ရေရရှိရန် ကြားကာလတစ်ခုစီတွင် ကိန်းဂဏန်းတစ်ခု မည်မျှပေါ်လာသည်ကို ရေတွက်သည်-

ထို့နောက်၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို ဆုံးဖြတ်ရန်၊ ယခင်တန်ဖိုးများအားလုံး၏ ပကတိကြိမ်နှုန်းများနှင့် မေးခွန်းရှိ တန်ဖိုး၏ ပကတိအကြိမ်ရေကို ပေါင်းထည့်ပါ-

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း နှင့် တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း နှင့် ပွားများ နှိုင်းရ ကြိမ်နှုန်း အကြား ခြားနားချက် သည် စုစည်းမှု ကြိမ်နှုန်း အမျိုးအစား နှင့် သက်ဆိုင်ပါသည်။ စုဆောင်းထားသော ပကတိကြိမ်နှုန်းသည် ညီမျှခြင်း သို့မဟုတ် နိမ့်သောတန်ဖိုးများ၏ ပကတိကြိမ်နှုန်းများ၏ ပေါင်းလဒ်နှင့် ညီမျှပြီး၊

ထို့ကြောင့်၊ တိုးပွားလာသော အကြွင်းမဲ့ကြိမ်နှုန်းကို absolute frequency မှ တွက်ချက်ပြီး တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို relative frequency မှ တွက်ချက်ပါသည်။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းတွက်ချက်မှု၏ ဥပမာကို ဤနေရာတွင် ကြည့်ရှုနိုင်သည်-