အနုတ်လက္ခဏာ binomial နှင့် poisson- ဆုတ်ယုတ်မှုပုံစံကို ရွေးချယ်နည်း

Negative binomial regression နှင့် Poisson regression သည် discrete count outcomes ဖြင့် တုံ့ပြန်မှု variable ကို ကိုယ်စားပြုသောအခါတွင် အသုံးပြုသင့်သော ဆုတ်ယုတ်မှုပုံစံနှစ်မျိုးဖြစ်သည်။

ဤသည်မှာ သီးခြားရေတွက်ခြင်းရလဒ်များကို ကိုယ်စားပြုသည့် တုံ့ပြန်မှုကိန်းရှင်အချို့၏ ဥပမာများဖြစ်သည်-

• အချို့သော ပရိုဂရမ်တစ်ခုမှ ဘွဲ့ရကျောင်းသား အရေအတွက်
• လမ်းဆုံမှာ ယာဉ်မတော်တဆမှု အရေအတွက်
• မာရသွန်ပြိုင်ပွဲပြီးမြောက်သူအရေအတွက်
• လက်လီစတိုးဆိုင်တွင် ပေးထားသော လတစ်လအတွင်း ပြန်ရရှိသည့်အရေအတွက်

ကွဲလွဲမှုသည် ခန့်မှန်းခြေအားဖြင့် ညီမျှပါက၊ Poisson ဆုတ်ယုတ်မှုပုံစံသည် ယေဘုယျအားဖြင့် ဒေတာအတွဲတစ်ခုနှင့် ကိုက်ညီပါသည်။

သို့သော်၊ ကွဲလွဲမှုသည် ပျမ်းမျှထက် သိသိသာသာကြီးနေပါက၊ အနုတ်လက္ခဏာ binomial regression မော်ဒယ်သည် ယေဘုယျအားဖြင့် ဒေတာကို ပိုမိုကောင်းမွန်စွာ ကိုက်ညီနိုင်မည်ဖြစ်သည်။

Poisson regression သို့မဟုတ် negative binomial regression သည် ပေးထားသော data set တစ်ခုအတွက် ပိုသင့်လျော်မှု ရှိမရှိ ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းနှစ်ခု ရှိပါသည်။

1. လက်ကျန်မြေကွက်များ

ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုမှ ခန့်မှန်းတန်ဖိုးများနှင့် စံသတ်မှတ်ထားသော အကြွင်းအကျန်များ၏ကွက်ကွက်တစ်ခုကို ဖန်တီးနိုင်သည်။

စံသတ်မှတ်ထားသောကျန်နေသေးသောအများစုသည် -2 နှင့် 2 ကြားဖြစ်ပါက Poisson ဆုတ်ယုတ်မှုပုံစံသည် သင့်လျော်ပါသည်။

သို့သော်၊ အကြွင်းအကျန်များစွာသည် ဤဘောင်အပြင်ဘက်တွင် ကျရောက်ပါက၊ အနုတ်လက္ခဏာ binomial ဆုတ်ယုတ်မှုပုံစံသည် ပိုမိုကောင်းမွန်သော အံဝင်ခွင်ကျဖြစ်စေနိုင်ဖွယ်ရှိသည်။

2. ဖြစ်နိုင်ခြေအချိုးစမ်းသပ်မှု

Poisson regression model နှင့် negative binomial regression model ကို တူညီသော data set တွင် တပ်ဆင်နိုင်ပြီး ဖြစ်နိုင်ခြေ အချိုးစမ်းသပ်မှုကို လုပ်ဆောင်နိုင်ပါသည်။

အကယ်၍ စမ်းသပ်မှု၏ p-တန်ဖိုးသည် အချို့သော အရေးပါမှုအဆင့် (ဥပမာ 0.05) အောက်တွင် ရှိနေပါက၊ အနုတ်လက္ခဏာ binomial regression မော်ဒယ်သည် သိသိသာသာ ပိုမိုကောင်းမွန်သော အံဝင်ခွင်ကျဖြစ်ကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည်။

အောက်ပါဥပမာသည် ပေးထားသောဒေတာအစုံအတွက် Poisson regression သို့မဟုတ် negative binomial regression model ကိုအသုံးပြုခြင်းသည် ပိုကောင်းကြောင်း ဆုံးဖြတ်ရန် R တွင် ဤနည်းပညာနှစ်ခုကို အသုံးပြုနည်းကို ပြသထားသည်။

ဥပမာ- အနှုတ်နှစ်အမည်ဆုတ်ယုတ်မှုနှင့် Poisson ဆုတ်ယုတ်မှု

အထက်တန်းကျောင်း ဘေ့စ်ဘောကစားသမားတစ်ဦးသည် ၎င်း၏ကျောင်းဌာနခွဲ (“ A” , “ B” သို့မဟုတ် “ C” ) နှင့် ၎င်း၏ကျောင်းအဆင့်အပေါ်အခြေခံ၍ ခရိုင်တစ်ခုတွင် ပညာသင်ဆုမည်မျှရရှိသည်ကို ကျွန်ုပ်တို့သိချင်သည်ဆိုပါစို့။ တက္ကသိုလ်ဝင်ခွင့်စာမေးပွဲ (0 မှ 100)။ )

အနုတ်လက္ခဏာ binomial regression model သို့မဟုတ် Poisson regression model သည် data နှင့် ပိုမိုကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။

အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

အောက်ဖော်ပြပါ ကုဒ်သည် ဘေ့စ်ဘောကစားသမား 1,000 ၏ ဒေတာများ ပါဝင်သော ကျွန်ုပ်တို့နှင့် လုပ်ဆောင်မည့် ဒေတာအတွဲကို ဖန်တီးသည်-

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

အဆင့် 2- Poisson ဆုတ်ယုတ်မှုပုံစံနှင့် အနုတ်လက္ခဏာ binomial regression မော်ဒယ်ကို ကိုက်ညီပါ။

အောက်ပါကုဒ်သည် ဒေတာနှင့် Poisson ဆုတ်ယုတ်မှုပုံစံနှင့် အနုတ်လက္ခဏာ binomial regression မော်ဒယ်နှစ်ခုလုံးကို မည်ကဲ့သို့ ကိုက်ညီရမည်ကို ပြသသည်-

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

အဆင့် 3- ကျန်ရှိသော မြေကွက်များကို ဖန်တီးပါ။

အောက်ဖော်ပြပါ ကုဒ်သည် မော်ဒယ်နှစ်မျိုးလုံးအတွက် ကျန်ရှိသော မြေကွက်များကို မည်သို့ထုတ်လုပ်ရမည်ကို ပြသထားသည်။

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

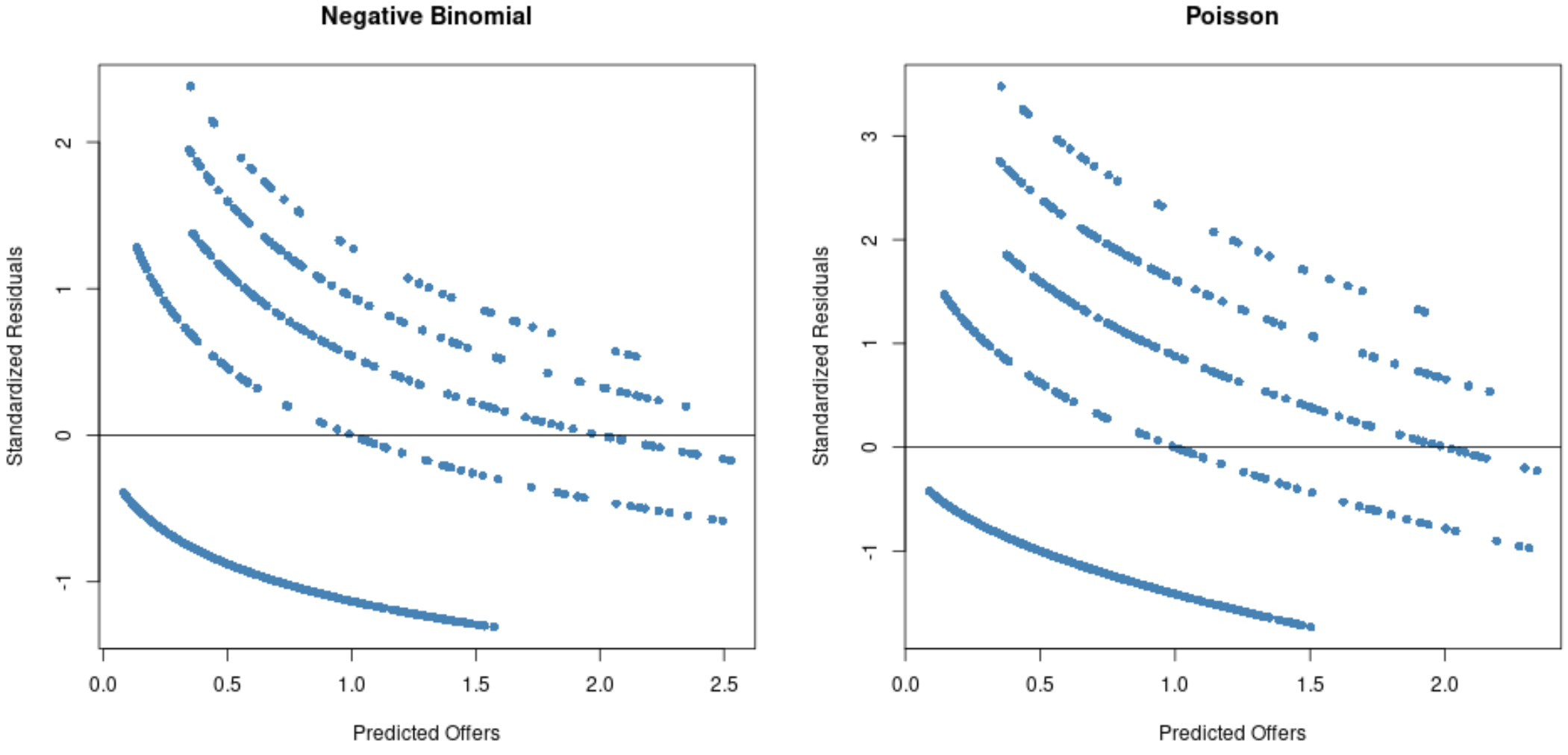
ဂရပ်များမှ၊ အကြွင်းအကျန်များသည် Poisson ဆုတ်ယုတ်မှုပုံစံအတွက် (အချို့အကြွင်းအကျန်များသည် 3 ထက်ကျော်လွန်နေသည်ကို သတိပြုပါ) အနုတ် binomial regression မော်ဒယ်နှင့် နှိုင်းယှဉ်ပါက ပိုမိုပျံ့နှံ့နေသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ဤမော်ဒယ်၏ အကြွင်းအကျန်များသည် သေးငယ်သောကြောင့် အနုတ်လက္ခဏာ binomial regression model သည် ပို၍သင့်လျော်ကြောင်း လက္ခဏာတစ်ရပ်ဖြစ်သည်။

အဆင့် 4- ဖြစ်နိုင်ခြေအချိုးကို စမ်းသပ်ပါ။

နောက်ဆုံးတွင်၊ ဆုတ်ယုတ်မှုပုံစံနှစ်ခု၏ အံဝင်ခွင်ကျဖြစ်သော ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် ဖြစ်နိုင်ခြေအချိုးစမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်-

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

စစ်ဆေးမှု၏ p-value သည် 3.508072e-29 ဖြစ်ပြီး 0.05 ထက် သိသိသာသာ နည်းပါသည်။

ထို့ကြောင့်၊ အနုတ်လက္ခဏာ binomial regression model သည် Poisson regression model နှင့် နှိုင်းယှဉ်ပါက data နှင့် သိသိသာသာ ပိုမိုကိုက်ညီကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်မည်ဖြစ်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုမိတ်ဆက်
Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်