Multinomial test ဆိုတာ ဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

အမျိုးအစားအလိုက် ကိန်းရှင်တစ်ခုသည် တွေးခေါ်မှုဆိုင်ရာ ဖြန့်ဝေမှုနောက်တွင်ရှိမရှိ ဆုံးဖြတ်ရန် ဘက်စုံအမည်စမ်းသပ်မှုကို အသုံးပြုသည်။

ဤစမ်းသပ်မှုသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည် ။

H ₀ : အမျိုးအစားကွဲပြားသော ကိန်းရှင်တစ်ခုသည် တွေးခေါ်မှုဆိုင်ရာ ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။

H _A : အမျိုးအစားကွဲပြားသောကိန်းရှင်သည် တွေးခေါ်မှုဖြန့်ဝေမှုကို မလိုက်နာပါ ။

စမ်းသပ်မှု၏ p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက (ဥပမာ α = 0.05)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး ကိန်းရှင်သည် တွေးခေါ်မှုဆိုင်ရာ ဖြန့်ဝေမှုကို မလိုက်နာကြောင်း ကောက်ချက်ချနိုင်သည်။

ကိန်းရှင်တစ်ခုသည် မတူညီသောရလဒ်များကို k ယူနိုင်သည့်အခါ ဤစမ်းသပ်မှုကို အသုံးပြုသည်။ အချို့သော အန်စာတုံးများ တရားမျှတခြင်း ရှိ၊ သေတ္တာကို လှိမ့်လိုက်သောအခါ၊ နံပါတ် (၁ မှ ၆) တစ်ခုစီတွင် ကျရောက်နိုင်ခြေသည် 1/6 ဖြစ်သည်။

သေခြင်းတရားသည် တရားမျှတမှု ရှိ၊ မရှိ စမ်းသပ်ရန်၊ ကျွန်ုပ်တို့သည် ၎င်းကို အကြိမ်များစွာ လှိမ့်ပြီး မတူညီသော နံပါတ်များပေါ်တွင် ကျရောက်သည့် အကြိမ်အရေအတွက်သည် ကျွန်ုပ်တို့ မျှော်လင့်ထားသည့်အရာနှင့် သိသိသာသာ ကွာခြားမှုရှိမရှိ ကြည့်ရှုနိုင်မည်ဖြစ်သည်။

အောက်ဖော်ပြပါနမူနာများသည် R စာရင်းအင်းပရိုဂရမ်းမင်းဘာသာစကားကို အသုံးပြု၍ အမည်မျိုးစုံစမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

ဥပမာ 1- Fair Dice

သေခြင်းတရားသည် တရားမျှတမှု ရှိမရှိ ဆုံးဖြတ်လိုသည်ဆိုပါစို့။ ဒါကို စမ်းသပ်ဖို့အတွက် အကြိမ် 30 လောက် လုပ်ဆောင်ပြီး ရလဒ်တစ်ခုစီရဲ့ ကြိမ်နှုန်းကို မှတ်တမ်းတင်ပါတယ်။ အောက်ပါဇယားသည် ရလဒ်များကို ပြသသည်-

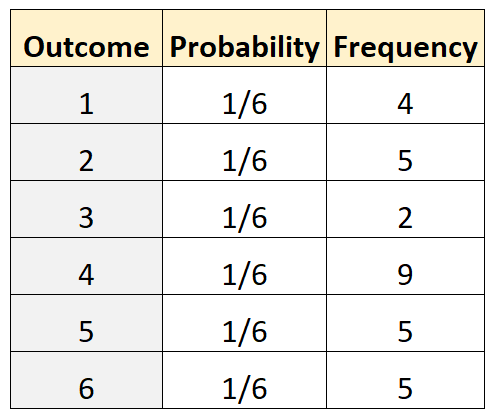
Multinomial စမ်းသပ်မှုပြုလုပ်ရန် R ရှိ အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

စမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.4306 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်မည်မဟုတ်ပါ။ ဒါကြောင့် အန်စာတုံးတွေက မတရားဘူးလို့ ပြောဖို့ လုံလောက်တဲ့ အထောက်အထား မရှိပါဘူး။

ဥပမာ 2- ထုတ်ကုန်ရောင်းအား

စတိုးဆိုင်ပိုင်ရှင်တစ်ဦးသည် မတူညီသော ကုန်ပစ္စည်းလေးမျိုးမှ ဝယ်ယူသူအရေအတွက် တူညီသည်ဟု ယူဆသည်ဆိုပါစို့။ ၎င်းကို စမ်းသပ်ရန်၊ ၎င်းသည် သတ်မှတ်ရက်သတ္တပတ်အတွင်း ထုတ်ကုန်တစ်ခုစီကို ဝယ်ယူသည့် သုံးစွဲသူအရေအတွက်ကို မှတ်တမ်းတင်ထားသည်။ အောက်ပါဇယားသည် ရလဒ်များကို ပြသသည်-

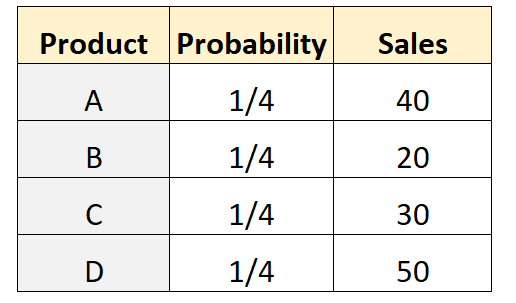
ဤဒေတာအတွဲတွင် အမည်ပေါင်းများစွာ စမ်းသပ်မှုပြုလုပ်ရန် R ရှိ အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

စာမေးပွဲ၏ p-တန်ဖိုးသည် 0.00226 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ပါမည်။ ဒါကြောင့် ကုန်ပစ္စည်းတစ်ခုစီအတွက် ရောင်းအားမညီမျှဘူးလို့ ပြောဖို့ လုံလောက်တဲ့ အထောက်အထားရှိပါတယ်။

ဥပမာ 3- အိတ်ထဲတွင် မာဘယ်လ်များ

အိတ်တစ်ခုမှ အနီရောင်၊ အစိမ်း သို့မဟုတ် ခရမ်းရောင် စကျင်ကျောက်ကို ရွေးချယ်ရန် ဖြစ်နိုင်ခြေမှာ 0.2၊ 0.5 နှင့် 0.3 အသီးသီးဖြစ်ကြောင်း Tom က ဖော်ပြသည်။ ဒါကို စမ်းသပ်ဖို့အတွက် သူ့သူငယ်ချင်း Mike ဟာ အိတ်ထဲကို ရောက်သွားပြီး မတူညီတဲ့ အကြိမ် 100 ရှိတဲ့ စကျင်ကျောက်တစ်လုံးကို ဆွဲထုတ်လိုက်ပါတယ်။ အောက်ပါဇယားသည် ရလဒ်များကို ပြသသည်-

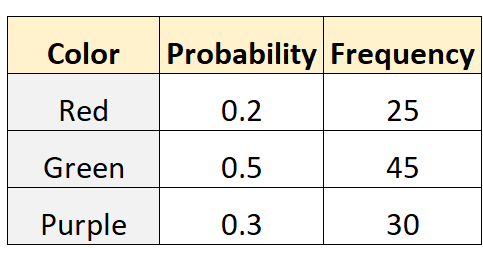
ဤဒေတာအတွဲတွင် အမည်ပေါင်းများစွာ စမ်းသပ်မှုပြုလုပ်ရန် R ရှိ အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

စမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.3999 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်မည်မဟုတ်ပါ။ ထို့ကြောင့် အိတ်အတွင်းမှ စကျင်ကျောက်များ ဖြန့်ဖြူးမှုသည် Tom မှ သတ်မှတ်ထားသည့် အထောက်အထားများနှင့် ကွဲလွဲသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Multinomial Distribution နိဒါန်း
Multinomial Distribution Calculator