စာရင်းဇယားများတွင် ဘီတာအဆင့်သည် အဘယ်နည်း။ (အဓိပ္ပါယ် & #038; ဥပမာ)

စာရင်းဇယားများတွင်၊ လူဦးရေကန့်သတ်ချက် တစ်ခုနှင့် ပတ်သက်သော ယူဆချက်သည် မှန်ကန်ခြင်းရှိမရှိ ဆုံးဖြတ်ရန် သီအိုရီစစ်ဆေးမှုကို အသုံးပြုပါသည်။

သီအိုရီစမ်းသပ်မှုတစ်ခုတွင် အောက်ဖော်ပြပါ အယူအဆနှစ်ခု အမြဲရှိသည်။

Null hypothesis (H ₀ ) : နမူနာဒေတာသည် လူဦးရေကန့်သတ်ချက်နှင့်ပတ်သက်သော လွှမ်းမိုးထားသောယုံကြည်ချက်နှင့် ကိုက်ညီပါသည်။

Alternative Hypothesis ( _HA ) : null hypothesis တွင်ဖော်ပြထားသော ယူဆချက်သည် မမှန်ကြောင်း နမူနာဒေတာက အကြံပြုထားသည်။ တစ်နည်းဆိုရသော်၊ ကျပန်းမဟုတ်သော အကြောင်းအရင်းသည် ဒေတာကို လွှမ်းမိုးပါသည်။

ကျွန်ုပ်တို့သည် သီအိုရီစမ်းသပ်မှုတစ်ခုကို ပြုလုပ်သည့်အခါတိုင်းတွင် ဖြစ်နိုင်သည့်ရလဒ် လေးမျိုး အမြဲရှိနေသည်-

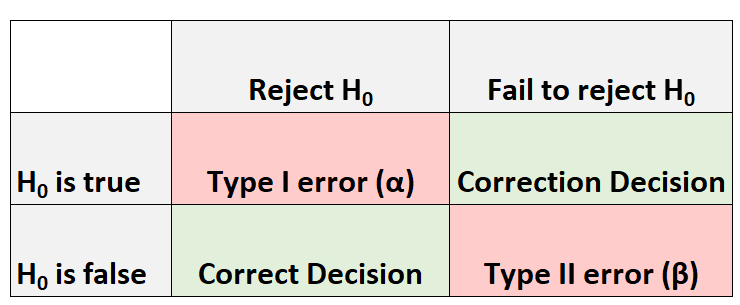
ကျွန်ုပ်တို့လုပ်နိုင်သော အမှားနှစ်မျိုးရှိသည်။

• Type I error- အမှန်တကယ်မှန်သည့်အခါ null hypothesis ကို ငြင်းပယ်ပါသည်။ ဤအမှားမျိုးကျူးလွန်ခြင်း၏ ဖြစ်နိုင်ခြေကို α ကို ရည်ညွှန်းသည်။
• အမျိုးအစား II အမှား- အမှန်မှာ မှားယွင်းနေသည့်အခါ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဤအမှားမျိုးကျူးလွန်ခြင်း၏ ဖြစ်နိုင်ခြေကို β မှတ်သားထားသည်။

အယ်လ်ဖာနှင့် ဘီတာကြား ဆက်နွယ်မှု

အကောင်းဆုံးမှာ၊ သုတေသီများသည် Type I အမှားပြုလုပ်ရန် ဖြစ်နိုင်ခြေ နှင့် Type II အမှားပြုလုပ်နိုင်ခြေကို နည်းပါးစေလိုပါသည်။

သို့သော် ဤဖြစ်နိုင်ခြေနှစ်ခုကြားတွင် ညှိနှိုင်းမှုတစ်ခုရှိသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် အယ်လ်ဖာအဆင့်ကို လျှော့ချပါက၊ ၎င်းသည် အမှန်တကယ်မှန်သည့်အခါ null hypothesis ကို ငြင်းပယ်နိုင်ခြေကို လျှော့ချနိုင်သော်လည်း ၎င်းသည် အမှန်တကယ်တွင် beta အဆင့်ကို တိုးစေသည် – မှားယွင်းသည့်အခါ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်သည့် ဖြစ်နိုင်ခြေကို လျှော့ချနိုင်သည်။

ပါဝါနှင့် ဘီတာကြား ဆက်နွယ်မှု

သီအိုရီစမ်းသပ်မှုတစ်ခု၏ ပါဝါသည် အကျိုးသက်ရောက်မှု သို့မဟုတ် ကွာခြားချက် အမှန်တကယ်ရှိနေသည့်အခါ အကျိုးသက်ရောက်မှု သို့မဟုတ် ကွာခြားချက်ကို ရှာဖွေတွေ့ရှိနိုင်ခြေကို ရည်ညွှန်းသည်။ တစ်နည်းဆိုရသော် ၎င်းသည် မှားယွင်းသော null hypothesis ကို မှန်ကန်စွာ ငြင်းပယ်ခြင်း၏ ဖြစ်နိုင်ခြေဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

ပါဝါ = 1 – β

ယေဘူယျအားဖြင့်၊ သုတေသီများသည် စမ်းသပ်မှုတစ်ခု၏ စွမ်းအားကို မြင့်မားစေလိုသောကြောင့် အကျိုးသက်ရောက်မှု သို့မဟုတ် ကွာခြားမှုရှိပါက ၎င်းကို စမ်းသပ်သိရှိနိုင်မည်ဖြစ်သည်။

အထက်ဖော်ပြပါ ညီမျှခြင်းမှ၊ စမ်းသပ်မှုတစ်ခု၏ ပါဝါတိုးမြှင့်ရန် အကောင်းဆုံးနည်းလမ်းမှာ ဘီတာအဆင့်ကို လျှော့ချရန်ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ဘီတာအဆင့်ကို လျှော့ချရန် အကောင်းဆုံးနည်းလမ်းမှာ နမူနာအရွယ်အစားကို တိုးမြှင့်ရန်ဖြစ်သည်။

အောက်ဖော်ပြပါနမူနာများသည် သီအိုရီစမ်းသပ်မှုတစ်ခု၏ ဘီတာအဆင့်ကို တွက်ချက်နည်းကို ပြသပြီး နမူနာအရွယ်အစားကို တိုးမြှင့်ရခြင်းမှာ ဘီတာအဆင့်ကို လျှော့ချနိုင်သည်ကို သရုပ်ပြသည်။

ဥပမာ 1- Hypothesis Test အတွက် Beta ကို တွက်ချက်ပါ။

စက်ရုံတစ်ခုတွင်ထုတ်လုပ်သည့်ဝစ်ဂျက်များ၏ပျမ်းမျှအလေးချိန်သည် 500 အောင်စအောက်ရှိမရှိ သုတေသီတစ်ဦးစမ်းသပ်လိုသည်ဆိုပါစို့။ အလေးများ၏စံသွေဖည်မှုသည် 24 အောင်စဖြစ်သည်ကိုကျွန်ုပ်တို့သိကြပြီးသုတေသီသည်ကျပန်းနမူနာ 40 ဝဒ်များကိုစုဆောင်းရန်ဆုံးဖြတ်သည်။

၎င်းသည် α = 0.05 တွင် အောက်ဖော်ပြပါ အယူအဆကို နားလည်နိုင်လိမ့်မည် ။

• H ₀ : µ = 500
• H _A : μ < 500

ယခု ထုတ်လုပ်လိုက်သော ဝစ်ဂျက်များ၏ ပျမ်းမျှအလေးချိန်မှာ အမှန်တကယ် 490 အောင်စဖြစ်ကြောင်း စိတ်ကူးကြည့်ပါ။ တစ်နည်းဆိုရသော် null hypothesis ကို ပယ်ချရမည်။

ဘီတာအဆင့်ကို တွက်ချက်ရန် အောက်ပါအဆင့်များကို ကျွန်ုပ်တို့သုံးနိုင်သည် – အမှန်စင်စစ် ပယ်ချသင့်သည့်အခါ null hypothesis ကို ငြင်းပယ်ခြင်းမပြုနိုင်သည့် ဖြစ်နိုင်ခြေ-

အဆင့် 1- ငြင်းပယ်ခြင်းမပြုသည့် ဒေသကို ရှာပါ။

အရေးကြီးသော Z တန်ဖိုးဂဏန်းတွက်စက်အရ၊ α = 0.05 တွင် ဘယ်ဘက်အရေးပါသောတန်ဖိုးသည် -1.645 ဖြစ်သည်။

အဆင့် 2- ကျွန်ုပ်တို့ ငြင်းပယ်ရန် ပျက်ကွက်မည့် အနည်းဆုံး နမူနာကို ရှာပါ။

စမ်းသပ်စာရင်းအင်းကို z = ( x – μ) / (s/ √n ) အဖြစ် တွက်ချက်သည်။

ထို့ကြောင့်၊ နမူနာဆိုလိုမှုအတွက် ဤညီမျှခြင်းကို ကျွန်ုပ်တို့ဖြေရှင်းနိုင်သည်-

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/ √40 )
• x = ၄၉၃.၇၅၈

အဆင့် 3- အနည်းဆုံးနမူနာဆိုလိုသည် အမှန်တကယ်ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

ဤဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

• P(Z ≥ (493.758 – 490) / (24/√ 40 ))
• P(Z ≥ 0.99)

ပုံမှန် CDF ဂဏန်း တွက်စက်အရ Z ≥ 0.99 ဖြစ်နိုင်ခြေသည် 0.1611 ဖြစ်သည်။

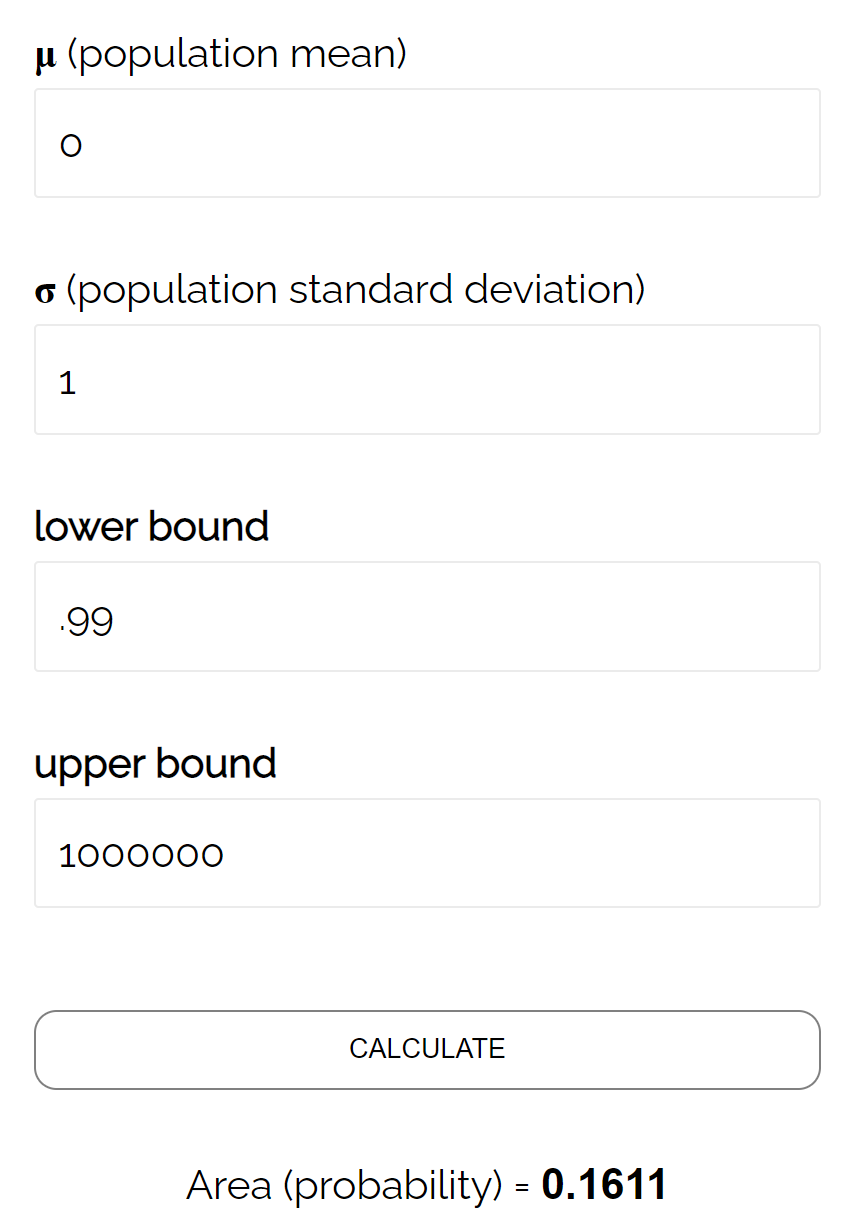
ထို့ကြောင့် ဤစစ်ဆေးမှုအတွက် ဘီတာအဆင့်သည် β = 0.1611 ဖြစ်သည်။ ဆိုလိုသည်မှာ အမှန်တကယ် ပျမ်းမျှ 490 အောင်စဖြစ်လျှင် ခြားနားချက်ကို ဖော်ထုတ်ရန် 16.11% ဖြစ်နိုင်ခြေရှိသည်။

ဥပမာ 2- ပိုကြီးသောနမူနာအရွယ်အစားဖြင့် စမ်းသပ်မှုအတွက် ဘီတာတွက်ချက်ပါ။

ယခု သုတေသီသည် အတိအကျတူညီသော ယူဆချက်စမ်းသပ်မှုကို လုပ်ဆောင်သည်ဆိုပါစို့၊ သို့သော် ၎င်းအစား n = 100 ဝစ်ဂျက်များကို နမူနာကို အသုံးပြုသည်။ ဤစမ်းသပ်မှုအတွက် ဘီတာအဆင့်ကို တွက်ချက်ရန် တူညီသော အဆင့်သုံးဆင့်ကို ထပ်ခါတလဲလဲ လုပ်ဆောင်နိုင်သည်-

အဆင့် 1- ငြင်းပယ်ခြင်းမပြုသည့် ဒေသကို ရှာပါ။

အရေးကြီးသော Z တန်ဖိုးဂဏန်းတွက်စက်အရ၊ α = 0.05 တွင် ဘယ်ဘက်အရေးပါသောတန်ဖိုးသည် -1.645 ဖြစ်သည်။

အဆင့် 2- ကျွန်ုပ်တို့ ငြင်းပယ်ရန် ပျက်ကွက်မည့် အနည်းဆုံး နမူနာကို ရှာပါ။

စမ်းသပ်စာရင်းအင်းကို z = ( x – μ) / (s/ √n ) အဖြစ် တွက်ချက်သည်။

ထို့ကြောင့်၊ နမူနာဆိုလိုမှုအတွက် ဤညီမျှခြင်းကို ကျွန်ုပ်တို့ဖြေရှင်းနိုင်သည်-

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/√ 100 )
• x = 496.05

အဆင့် 3- အနည်းဆုံးနမူနာဆိုလိုသည် အမှန်တကယ်ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

ဤဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

• P(Z ≥ (496.05 – 490) / (24/√ 100 ))
• P(Z ≥ 2.52)

ပုံမှန် CDF ဂဏန်း တွက်စက်အရ Z ≥ 2.52 ဖြစ်နိုင်ခြေသည် 0.0059 ဖြစ်သည်။

ထို့ကြောင့် ဤစစ်ဆေးမှုအတွက် ဘီတာအဆင့်သည် β = 0.0059 ဖြစ်သည်။ ဆိုလိုသည်မှာ အမှန်တကယ် ပျမ်းမျှ 490 အောင်စ ဖြစ်ပါက ခြားနားချက်ကို ဖော်ထုတ်ရန် 0.59% သာ အခွင့်အလမ်း ရှိနေပါသည်။

နမူနာအရွယ်အစားကို 40 မှ 100 အထိ တိုးမြှင့်ခြင်းဖြင့် သုတေသီသည် ဘီတာအဆင့်ကို 0.1611 မှ 0.0059 သို့ လျှော့ချနိုင်ခဲ့ကြောင်း သတိပြုပါ။

အပိုဆု- စမ်းသပ်မှုတစ်ခု၏ ဘီတာအဆင့်ကို အလိုအလျောက်တွက်ချက်ရန် ဤအမျိုးအစား II အမှားဂဏန်းတွက်စက်ကို အသုံးပြုပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Hypothesis Testing နိဒါန်း
Null Hypothesis ရေးနည်း (ဥပမာ ၅ ခု)
P တန်ဖိုးများနှင့် စာရင်းအင်းဆိုင်ရာ အရေးပါမှုဆိုင်ရာ ရှင်းလင်းချက်