R ဖြင့် ပါဝါဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း (တစ်ဆင့်ပြီးတစ်ဆင့်)
Power regression သည် အောက်ဖော်ပြပါ ပုံစံဖြင့် အသုံးပြုသော linear မဟုတ်သော ဆုတ်ယုတ်မှု အမျိုးအစားတစ်ခုဖြစ်သည်။
y = axb
ရွှေ-
- y- တုံ့ပြန်မှု ကိန်းရှင်
- x- ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်
- a, b- x နှင့် y အကြား ဆက်နွယ်မှုကို ဖော်ပြသည့် ဆုတ်ယုတ်မှုကိန်းဂဏန်းများ
ဤဆုတ်ယုတ်မှုအမျိုးအစားအား တုံ့ပြန်မှု ကိန်းရှင် သည် ပါဝါတစ်ခုသို့ မြှင့်တင်ပေးသည့် ခန့်မှန်းကိန်းရှင်နှင့် ညီမျှသည့် အခြေအနေများကို စံပြရန်အတွက် အသုံးပြုသည်။
အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် R တွင် ပေးထားသည့် ဒေတာအတွဲအတွက် ပါဝါဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။
အဆင့် 1: ဒေတာကိုဖန်တီးပါ။
ပထမဦးစွာ၊ x နှင့် y ကိန်းရှင်နှစ်ခုအတွက် ဒေတာအတုဖန်တီးကြပါစို့။
#create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)
အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။
ထို့နောက် x နှင့် y အကြား ဆက်နွယ်မှုကို မြင်သာစေရန် scatterplot တစ်ခုကို ဖန်တီးကြပါစို့။
#create scatterplot
plot(x, y)
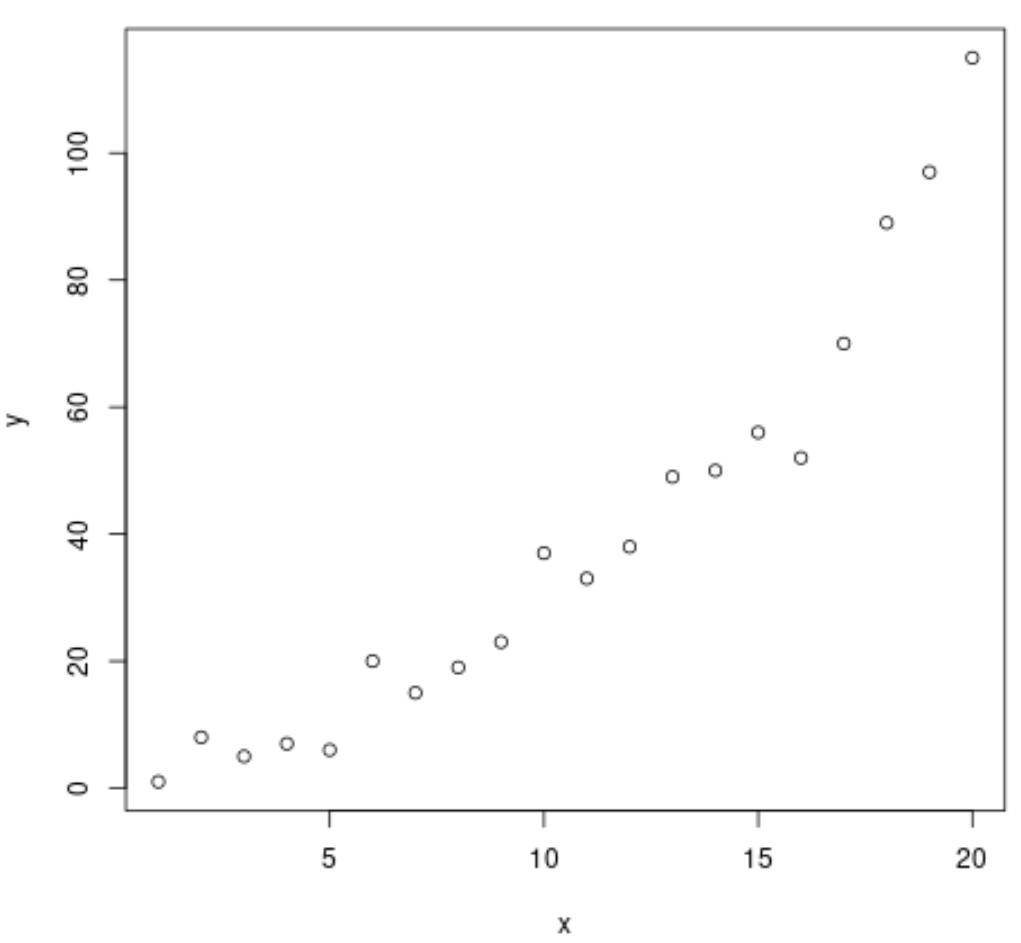
ဂရပ်သည် ကိန်းရှင်နှစ်ခုကြားတွင် ပြတ်သားသော ပါဝါဆက်နွယ်မှုရှိကြောင်း ပြသသည်။ ထို့ကြောင့်၊ linear regression model ထက် data နှင့် power regression equation ကို အံဝင်ခွင်ကျဖြစ်ပုံရသည်။
အဆင့် 3- ပါဝါဆုတ်ယုတ်မှုပုံစံကို အံကိုက်လုပ်ပါ။
ထို့နောက်၊ R သည် တုံ့ပြန်မှု ပြောင်းလဲနိုင်သော မှတ်တမ်းနှင့် မော်ဒယ်နှင့် အံဝင်ခွင်ကျဖြစ်သည့်အခါ ကြိုတင်ခန့်မှန်းနိုင်သော ပြောင်းလဲနိုင်သော မှတ်တမ်းကို အသုံးပြုသင့်သည်ဟု သတ်မှတ်ကာ ဒေတာနှင့် ဆုတ်ယုတ်မှုပုံစံကို အံကိုက်ရန်အတွက် lm() လုပ်ဆောင်ချက်ကို အသုံးပြုပါမည်။
#fit the model model <- lm(log(y)~ log(x)) #view the output of the model summary(model) Call: lm(formula = log(y) ~ log(x)) Residuals: Min 1Q Median 3Q Max -0.67014 -0.17190 -0.05341 0.16343 0.93186 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.15333 0.20332 0.754 0.461 log(x) 1.43439 0.08996 15.945 4.62e-12 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.3187 on 18 degrees of freedom Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12
မော်ဒယ် တစ်ခုလုံး၏ F-value သည် 252.1 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် အလွန်နိမ့်နေပါသည် (4.619e-12)၊ မော်ဒယ်တစ်ခုလုံးသည် အသုံးဝင်ကြောင်း ညွှန်ပြပါသည်။
output table မှ coefficients များကို အသုံးပြု၍ fitted power regression equation သည်-
ln(y) = 0.15333 + 1.43439ln(x)
e ကို နှစ်ဖက်စလုံးတွင် အသုံးချခြင်းဖြင့် ညီမျှခြင်းအား အောက်ပါအတိုင်း ပြန်လည်ရေးသားနိုင်ပါသည်။
- y = e 0.15333 + 1.43439ln(x)
- y = 1.1657x 1.43439
ကြိုတင်ခန့်မှန်းကိန်းရှင်၏တန်ဖိုး၊ x ၏တန်ဖိုးအပေါ်အခြေခံ၍ တုံ့ပြန်မှုကိန်းရှင် y ကို ခန့်မှန်းရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။
ဥပမာ၊ x = 12 ဆိုရင် y က 41.167 ဖြစ်မယ် ၊
y = 1.1657(12) 1.43439 = 41.167
အပိုဆု- ပေးထားသော ခန့်မှန်းသူနှင့် တုံ့ပြန်မှု variable အတွက် ပါဝါဆုတ်ယုတ်မှုညီမျှခြင်းအား အလိုအလျောက်တွက်ချက်ရန် ဤအွန်လိုင်းပါဝါဆုတ်ယုတ်မှုဂဏန်းတွက်စက်ကို အသုံးပြုပါ။
ထပ်လောင်းအရင်းအမြစ်များ
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် exponential regression လုပ်ဆောင်နည်း
R တွင် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း