တစ်လမ်းမောင်း သို့မဟုတ် နှစ်လမ်း anova- ၎င်းတို့ကို မည်သည့်အချိန်တွင် အသုံးပြုရမည်နည်း။

ANOVA သည် “ ကွဲလွဲမှု၏ခွဲခြမ်းစိတ်ဖြာခြင်း” ၏အတိုကောက်ဖြစ်သော ANOVA ကို အမှီအခိုကင်းသော အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော သီးခြားအဖွဲ့များ၏ ဆိုလိုရင်းများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုပါသည်။

ANOVA ၏ အသုံးအများဆုံး အမျိုးအစား နှစ်မျိုးမှာ တစ်လမ်းသွား ANOVA နှင့် နှစ်လမ်း ANOVA ဖြစ်သည်။

တစ်လမ်းသွား ANOVA- အချက် တစ်ခုသည် တုံ့ပြန်မှုကိန်းရှင်အပေါ် မည်သို့အကျိုးသက်ရောက်သည်ကို ဆုံးဖြတ်ရန် အသုံးပြုသည်။

two-way ANOVA- အချက်နှစ်ချက်က တုံ့ပြန်မှုကိန်းရှင်အပေါ် အကျိုးသက်ရောက်ပုံကို ဆုံးဖြတ်ရန်နှင့် တုံ့ပြန်မှုကိန်းရှင်တွင် အချက်နှစ်ခုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

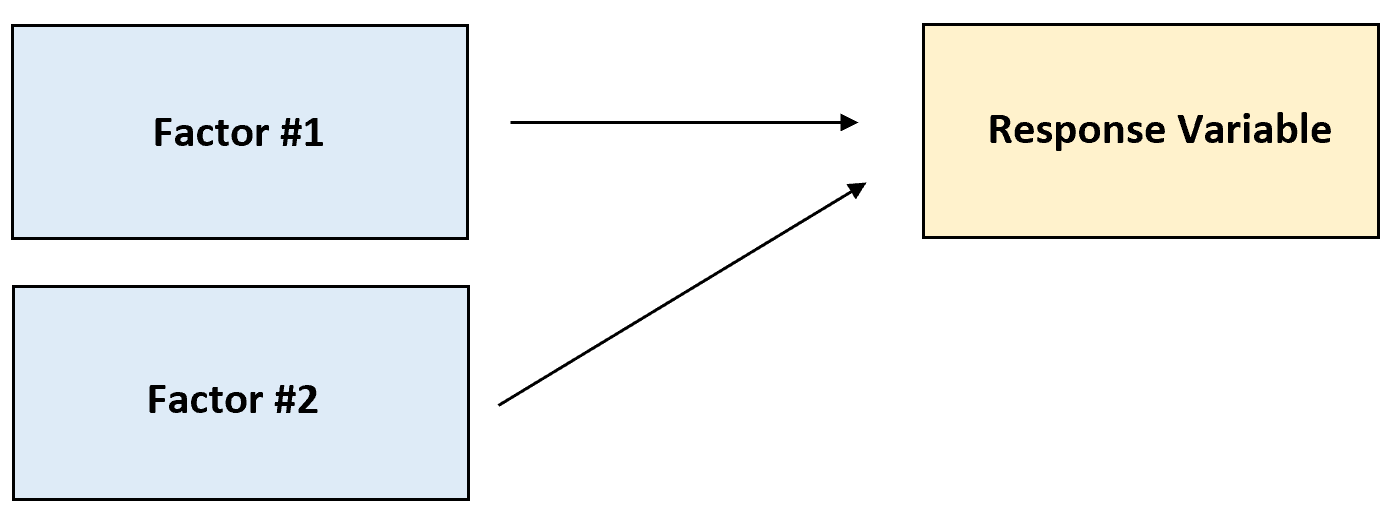
အောက်ဖော်ပြပါ ဥပမာများသည် ANOVA အမျိုးအစားတစ်ခုစီကို မည်သို့လုပ်ဆောင်ရမည်ကို ဥပမာပေးပါသည်။

ဥပမာ- တစ်လမ်းမောင်း ANOVA

မတူညီသော လေ့လာမှုနည်းပညာသုံးမျိုးတွင် မတူညီသော စာမေးပွဲရမှတ်များ ဖြစ်ပေါ်လာခြင်းရှိမရှိကို ပါမောက္ခတစ်ဦးက သိချင်သည်ဆိုပါစို့။ ၎င်းကိုစမ်းသပ်ရန်၊ လေ့လာမှုတစ်ခုတွင်ပါဝင်ရန်ကျောင်းသား 30 ကိုစုဆောင်းပြီးစာမေးပွဲအတွက်ပြင်ဆင်ရန်နည်းပညာသုံးမျိုးထဲမှတစ်ခုစီကိုကျပန်းတောင်းဆိုသည်။ တစ်လကြာပြီးနောက် ကျောင်းသားအားလုံး တူညီသော စာမေးပွဲကို ဖြေဆိုကြသည်။

ကျောင်းသားတစ်ဦးစီ၏ စာမေးပွဲရလဒ်များကို အောက်တွင် ဖော်ပြထားသည်။

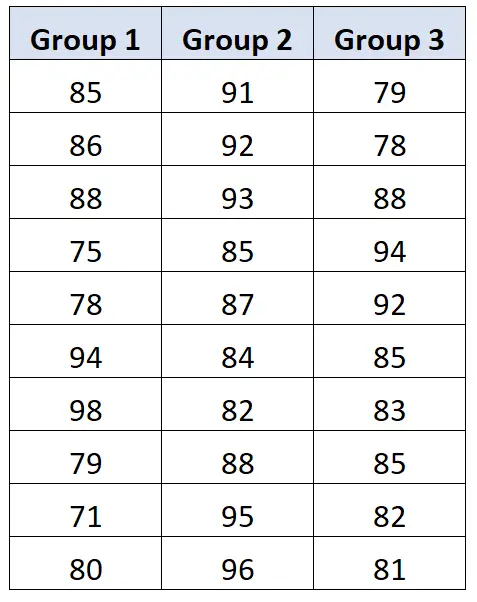
ပါမောက္ခသည် တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ပြီး အောက်ပါရလဒ်များကို ရရှိသည်-

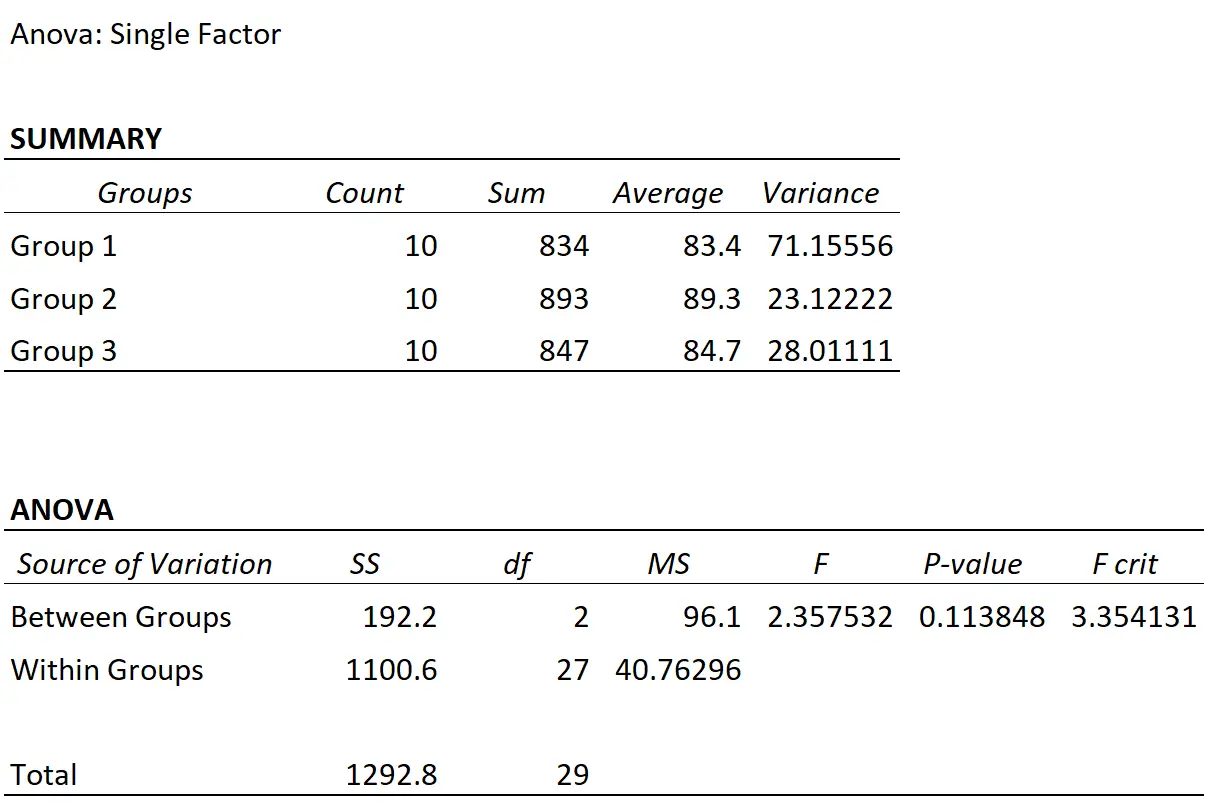
F-test statistic သည် 2.3575 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် 0.1138 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ လေ့လာမှုနည်းလမ်းသုံးခုသည် မတူညီသောပျမ်းမျှစာမေးပွဲရမှတ်များဆီသို့ ဦးတည်သည်ဟုဆိုရန် လုံလောက်သောအထောက်အထားမရှိပါ။

ဥပမာ- နှစ်လမ်းသွား ANOVA

ရုက္ခဗေဒပညာရှင်တစ်ဦးသည် နေရောင်ခြည်နှင့် ထိတွေ့မှုအကြိမ်ရေကြောင့် အပင်ကြီးထွားမှုအပေါ် လွှမ်းမိုးမှုရှိမရှိ သိချင်သည်ဆိုပါစို့။ အစေ့အစေ့ ၄၀ ကို စိုက်ပျိုးပြီး နေရောင်ခြည်နှင့် ရေလောင်းအကြိမ်ရေ မတူညီသော အခြေအနေများတွင် နှစ်လကြာ ကြီးထွားစေပါသည်။ နှစ်လကြာပြီးနောက် အပင်တစ်ပင်ချင်းစီ၏ အမြင့်ကို မှတ်တမ်းတင်သည်။ ရလဒ်များကို အောက်တွင် ပြထားသည်။

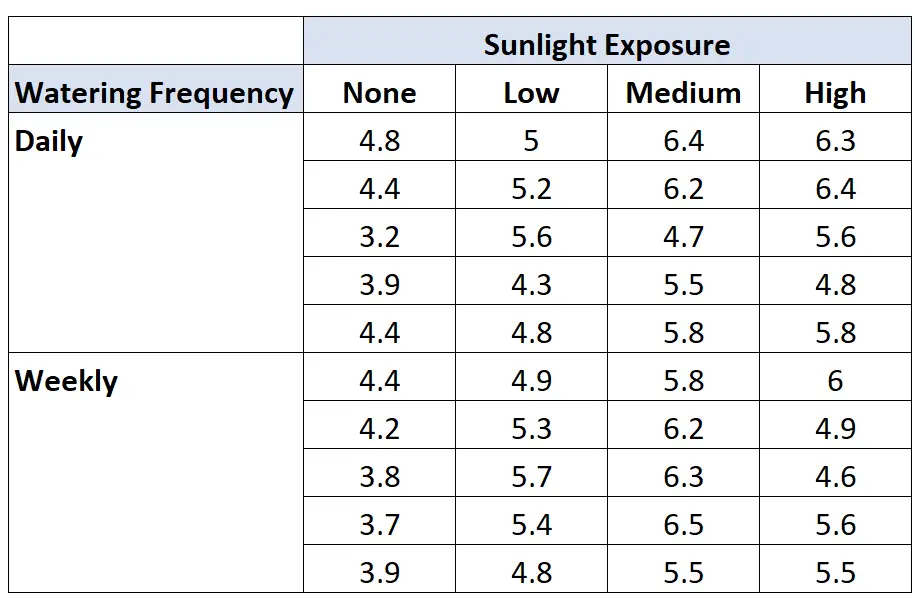
ပါမောက္ခသည် နှစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ပြီး အောက်ပါရလဒ်များကို ရရှိသည်။

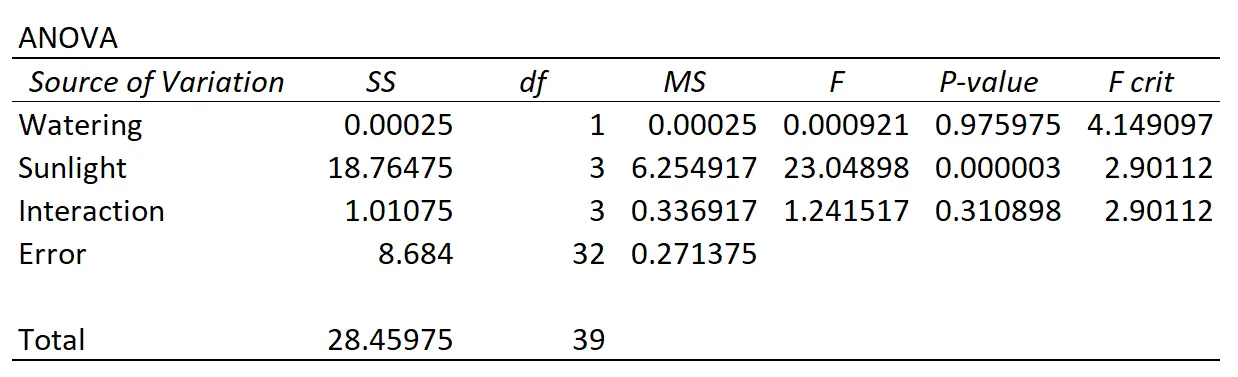
ဤသည်မှာ ရလဒ်များကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• ရေလောင်းအကြိမ်ရေနှင့် နေရောင်ခြည်ထိတွေ့မှုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုအတွက် p-တန်ဖိုးသည် 0.310898 ဖြစ်သည်။ ၎င်းသည် 0.05 alpha အဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်မဟုတ်ပါ။
• ရေလောင်းအကြိမ်ရေအတွက် p-တန်ဖိုးသည် 0.975975 ဖြစ်သည်။ ၎င်းသည် 0.05 alpha အဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်မဟုတ်ပါ။
• နေရောင်ခြည်ထိတွေ့မှုအတွက် p-တန်ဖိုးသည် 0.000003 ဖြစ်သည်။ ၎င်းသည် 0.05 ၏ alpha အဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်။

ဤရလဒ်များသည် အပင်အမြင့်အပေါ် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော အကျိုးသက်ရောက်မှုရှိသော တစ်ခုတည်းသောအချက်မှာ နေရောင်ခြည်နှင့်ထိတွေ့ခြင်းဖြစ်သည်ဟု ဖော်ပြသည်။

အပြန်အလှန်အကျိုးသက်ရောက်မှုမရှိသောကြောင့်၊ နေရောင်ခြည်ထိတွေ့မှုအကျိုးသက်ရောက်မှုသည် ရေလောင်းအကြိမ်ရေအဆင့်တိုင်းတွင် တသမတ်တည်းဖြစ်သည်။ ရိုးရိုးရှင်းရှင်းပြောရလျှင် အပင်တစ်ပင်ကို နေ့စဉ် သို့မဟုတ် အပတ်စဉ် ရေလောင်းသည်ဖြစ်စေ နေရောင်ထိတွေ့မှုသည် အပင်အပေါ် သက်ရောက်မှုမရှိပေ။

လက်တွေ့ကျကျ- မည်သည့် ANOVA ကို သင်အသုံးပြုသင့်သနည်း။

တစ်လမ်းသွား သို့မဟုတ် နှစ်လမ်း ANOVA ကိုသုံးသင့်သည့်အခါတွင် ပိုမိုကောင်းမွန်စွာနားလည်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။

ပြဿနာနံပါတ် ၁- စိုက်ပျိုးရေး

မတူကွဲပြားသော မြေသြဇာသုံးမျိုးက အထွက်နှုန်းမတူညီနိုင်သည်ကို တောင်သူတစ်ဦး သိချင်သည်။ ၎င်းကို စမ်းသပ်ရန်အတွက် မြေသြဇာတစ်မျိုးစီကို နယ်ပယ် ၁၀ ခုတွင် ဖြန့်ကျက်ပြီး စိုက်ပျိုးရာသီကုန်ဆုံးချိန်တွင် စုစုပေါင်းအထွက်နှုန်းကို တိုင်းတာသည်။

မတူညီသောမြေသြဇာများသည် မတူညီသောသီးနှံအထွက်နှုန်းကိုဖြစ်ပေါ်စေခြင်းရှိမရှိဆုံးဖြတ်ရန် ANOVA အမျိုးအစားကိုအသုံးပြုသင့်သည်။

အဖြေ- ဓာတ်မြေဩဇာတစ်ခုတည်းကိုသာ ကြည့်သောကြောင့် တစ်လမ်းမောင်း ANOVA ကို သုံးသင့်သည်။ တစ်လမ်းသွား ANOVA သည် ဓာတ်မြေသြဇာ အမျိုးအစားသုံးမျိုးကြား သီးနှံအထွက်နှုန်းတွင် ကိန်းဂဏန်း သိသိသာသာ ကွာခြားမှု ရှိ၊ မရှိ သူ့ကို ပြောပြနိုင်သည်။

ပြဿနာ #2- ဇီဝဗေဒ

ဇီဝဗေဒပညာရှင်တစ်ဦးသည် မတူညီသောမြေဆီလွှာအဆင့် (အနိမ့်၊ အလတ်စား၊ မြင့်) နှင့် ရေလောင်းကြိမ်နှုန်းများ (အပတ်စဉ်၊ လစဉ်) သည် အပင်တစ်ပင်၏ကြီးထွားမှုကို မည်ကဲ့သို့အကျိုးသက်ရောက်သည်ကို သိရှိလိုသည်။

ကွဲပြားသောနေရောင်ခြည်ထိတွေ့မှုနှင့် ရေလောင်းမှုအကြိမ်ရေ ပေါင်းစပ်မှုများသည် အပင်ကြီးထွားမှုအဆင့်ကို ကွဲပြားစေခြင်းရှိမရှိ ဆုံးဖြတ်ရန် ANOVA အမျိုးအစားကို အသုံးပြုသင့်သည်။

အဖြေ- နေရောင်ခြည်နှင့် ထိတွေ့မှု နှင့် ရေလောင်းအကြိမ်ရေ ဟူသော အချက်နှစ်ချက်ကို ကြည့်သောကြောင့် သူမသည် နှစ်လမ်းသွား ANOVA ကို အသုံးပြုသင့်သည်။ နှစ်လမ်းသွား ANOVA သည် အချက်တစ်ခုစီ၏ မတူညီသောအဆင့်များသည် အပင်ကြီးထွားမှုအပေါ် သက်ရောက်မှုရှိမရှိနှင့် အပင်ကြီးထွားမှုအပေါ် နေရောင်ခြည်နှင့် ရေလောင်းမှုအကြိမ်ရေကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုရှိမရှိတို့ကို ပြောပြနိုင်သည်။

ပြဿနာ နံပါတ် ၃- ဆေးဝါးများ

ဆေးသုတေသီတစ်ဦးသည် မတူညီသော ဆေးဝါးလေးမျိုးသည် လူနာများတွင် မတူညီသော သွေးပေါင်ချိန်ကို ပျမ်းမျှလျော့ကျစေခြင်း ရှိ၊မရှိ သိလိုသည်။ ၎င်းသည် လူနာအယောက် 20 ကို ကျပန်းတစ်လလျှင် ဆေးဝါးတစ်ခုစီအသုံးပြုရန် ကျပန်းသတ်မှတ်ပေးကာ လူနာတစ်ဦးစီတွင် သွေးပေါင်ချိန်ကျဆင်းမှုကို တိုင်းတာသည်။

မတူညီသော ဆေးလေးမျိုးသည် သွေးပေါင်ချိန်ကို လျှော့ချရာတွင် ကွဲပြားသော အာနိသင်ရှိမရှိ ဆုံးဖြတ်ရန် ANOVA အမျိုးအစားကို အသုံးပြုသင့်သည်။

အဖြေ- ဆေးအမျိုးအစားတစ်ခုတည်းကိုသာ ကြည့်သောကြောင့် တစ်ကြောင်း ANOVA ကို သုံးသင့်သည်။ တစ်လမ်းသွား ANOVA သည် ဆေးအမျိုးအစားလေးမျိုးကြားရှိ ပျမ်းမျှသွေးပေါင်ချိန်လျှော့ချမှုတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိကို ပြောပြနိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

တစ်လမ်းသွား ANOVA ကို ပိုမိုနားလည်ရန် အောက်ပါသင်ခန်းစာများကို အသုံးပြုပါ။

• One-Way ANOVA မိတ်ဆက်
• Excel တွင် One-Way ANOVA လုပ်ဆောင်နည်း
• တစ်လမ်းမောင်း ANOVA ကို R ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း။

နှစ်လမ်းသွား ANOVA ကို ပိုမိုနားလည်ရန် ဤသင်ခန်းစာများကို အသုံးပြုပါ။

• နှစ်လမ်းသွား ANOVA မိတ်ဆက်
• Excel တွင် Two-Way ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
• R ဖြင့် နှစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်နည်း