ကျန်နေတဲ့ကွာဟချက်ကဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

ကျန်ရှိသောကွဲလွဲမှု (တစ်ခါတစ်ရံ “ ရှင်းပြမထားသောကွဲလွဲမှု” ဟုခေါ်သည်) သည် မော်ဒယ်ကိန်းရှင်များဖြင့် ရှင်းပြ၍မရသော မော်ဒယ်တစ်ခုရှိ ကွဲလွဲမှုကို ရည်ညွှန်းသည်။

မော်ဒယ်တစ်ခု၏ ကျန်ရှိသောကွဲလွဲမှု မြင့်မားလေ၊ မော်ဒယ်သည် ဒေတာကွဲလွဲမှုကို ရှင်းပြနိုင်မှု နည်းပါးလေဖြစ်သည်။

ကွဲပြားသော ကိန်းဂဏန်းပုံစံနှစ်ခု၏ ရလဒ်များတွင် ကျန်ရှိသောကွဲလွဲမှု ပေါ်လာသည်-

1. ANOVA: အမှီအခိုကင်းသော အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော အဓိပ္ပါယ်များကို နှိုင်းယှဉ်ရန် အသုံးပြုသည်။

2. Regression- တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် ကြား ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် အသုံးပြုသည်။

အောက်ပါနမူနာများသည် ဤနည်းလမ်းတစ်ခုစီတွင် ကျန်ရှိသောကွဲလွဲမှုကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံကို ပြသထားသည်။

ANOVA မော်ဒယ်များတွင် ကျန်ရှိသောကွဲလွဲမှု

ကျွန်ုပ်တို့သည် ANOVA (“ ကွဲလွဲမှုကို ခွဲခြမ်းစိတ်ဖြာခြင်း” ) မော်ဒယ်နှင့် အံဝင်ခွင်ကျတိုင်း၊ ကျွန်ုပ်တို့သည် အောက်ပါပုံသဏ္ဍာန်ရှိသော ANOVA ဇယားကို အဆုံးသတ်လိုက်သည်-

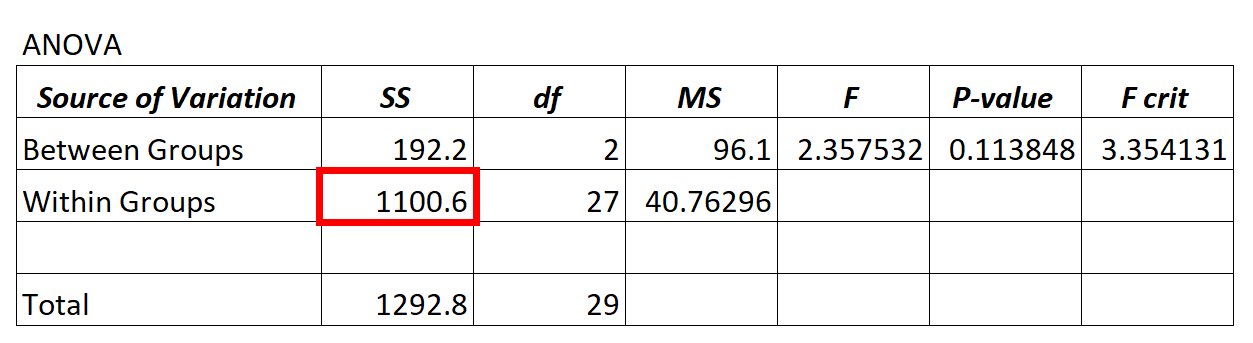
အုပ်စုတွင်း ကွဲလွဲမှုအတွက် ANOVA မော်ဒယ်မှ ကျန်ရှိသောတန်ဖိုးကို SS (“ စတုရန်းများ” ) ကော်လံတွင် တွေ့နိုင်သည်။

ဤတန်ဖိုးကို “ နှစ်ထပ်ကိန်းအမှားများပေါင်းလဒ်” ဟုလည်းခေါ်ပြီး အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်သည်-

Σ(X _ij – X _j ) ^၂

ရွှေ-

• Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• X _ij : အုပ်စု j ၏ စောင့်ကြည့် ^{လေ့လာမှု}
• X _j : အုပ်စု j ၏ ပျမ်းမျှ

အထက်ဖော်ပြပါ ANOVA မော်ဒယ်တွင် ကျန်ရှိသောကွဲလွဲမှုမှာ 1100.6 ဖြစ်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်ရပါသည်။

ဤကျန်နေသောကွဲလွဲမှုသည် “ မြင့်မားသည်” ကိုဆုံးဖြတ်ရန်၊ အုပ်စုများအတွင်းအတွက် ပျမ်းမျှစတုရန်းနှစ်ခုနှင့် အုပ်စုများကြားအတွက် ပျမ်းမျှနှစ်ထပ်ကိန်းများကို တွက်ချက်နိုင်ပြီး ANOVA ဇယားရှိ အလုံးစုံ F တန်ဖိုးကိုပေးသည့် နှစ်ခုကြားအချိုးကို ရှာဖွေနိုင်သည်။

• F = MS _enters /MS _in
• F = 96.1 / 40.76296
• F = 2.357

အထက်ပါ ANOVA ဇယားရှိ F တန်ဖိုးသည် 2.357 ဖြစ်ပြီး သက်ဆိုင်ရာ p တန်ဖိုးမှာ 0.113848 ဖြစ်သည်။ ဤ p-value သည် α = 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကိုငြင်းပယ်ရန် လုံလောက်သောအထောက်အထားမရှိပါ။

ဆိုလိုသည်မှာ ကျွန်ုပ်တို့ နှိုင်းယှဉ်နေသော အုပ်စုများကြား ပျမ်းမျှ ကွာခြားချက်မှာ သိသိသာသာ ကွာခြားသည်ဟု ဆိုရန် လုံလောက်သော သက်သေ မရှိပါ။

၎င်းသည် ANOVA မော်ဒယ်၏ ကျန်ရှိနေသော ကွဲလွဲမှုသည် မော်ဒယ် အမှန်တကယ် ရှင်းပြနိုင်သည့် ကွဲလွဲမှုနှင့် နှိုင်းယှဉ်ပါက မြင့်မားကြောင်း ကျွန်ုပ်တို့ကို ပြောပြသည်။

ဆုတ်ယုတ်မှုပုံစံများတွင် ကျန်ရှိသောကွဲလွဲမှု

ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင်၊ ကျန်ရှိသောကွဲလွဲမှုကို ခန့်မှန်းထားသည့်ဒေတာမှတ်များနှင့် စောင့်ကြည့်လေ့လာထားသည့်ဒေတာအချက်များကြားရှိခြားနားချက်များ၏နှစ်ထပ်ကိန်းများအဖြစ်သတ်မှတ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

Σ(ŷ _i – y _i ) ^၂

ရွှေ-

• Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• ŷ _i : ခန့်မှန်းထားသော ဒေတာအချက်များ
• y _i : စောင့်ကြည့်လေ့လာထားသော ဒေတာအချက်များ

ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို အံဝင်ခွင်ကျသောအခါတွင်၊ ကျွန်ုပ်တို့သည် များသောအားဖြင့် အောက်ပါအတိုင်း ရလဒ်ကို ရရှိသည်-

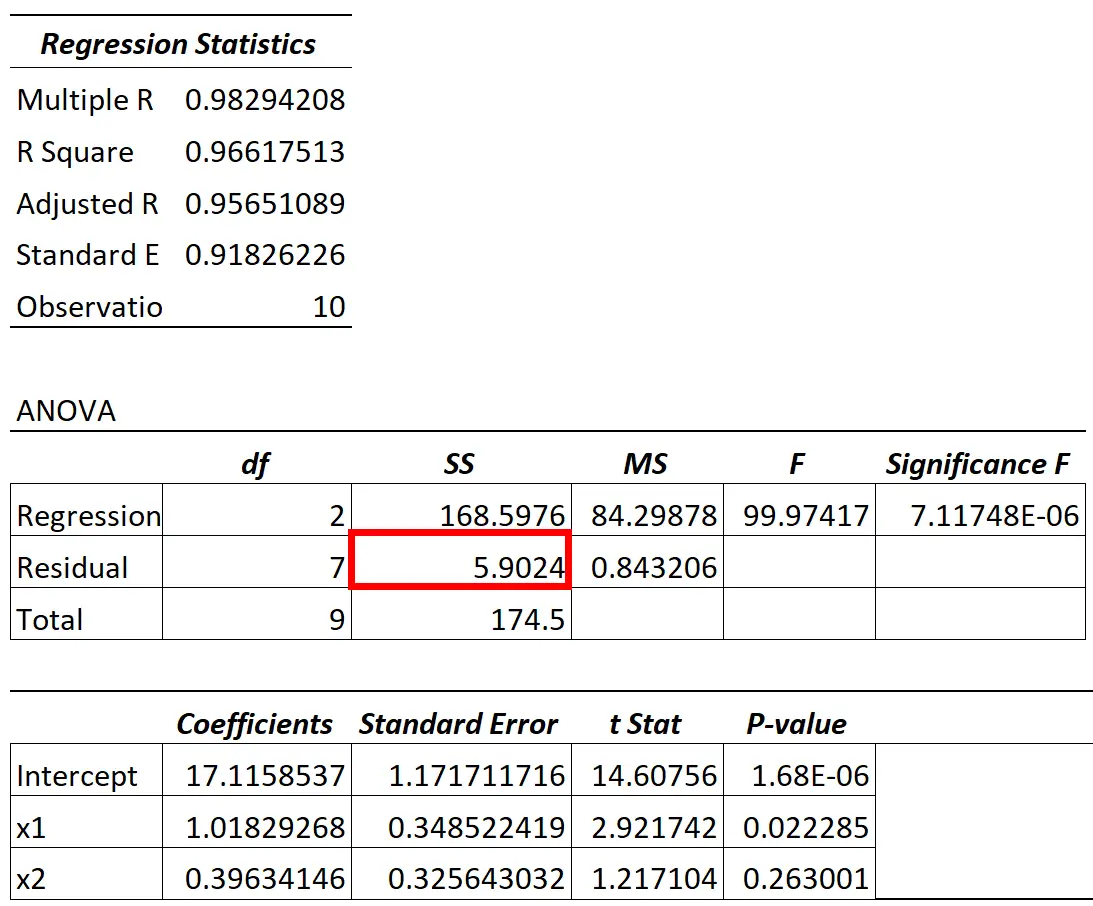
ANOVA မော်ဒယ်မှ ကျန်ရှိသော ကွဲလွဲမှုတန်ဖိုးကို SS (“ စတုရန်းများ” ) ကော်လံတွင် တွေ့ရှိနိုင်သည်။

မော်ဒယ်ရှိ အကြွင်းအကျန်ကွဲလွဲချက်နှင့် စုစုပေါင်းကွဲလွဲမှုအချိုးသည် မော်ဒယ်ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင်များမှ ရှင်းပြမရနိုင်သော တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှုရာခိုင်နှုန်းကို ပြောပြသည်။

ဥပမာအားဖြင့်၊ အထက်ဖော်ပြပါဇယားတွင်၊ ဤရာခိုင်နှုန်းကို အောက်ပါအတိုင်း တွက်ချက်ရမည်ဖြစ်ပါသည်။

• မရှင်းပြနိုင်သော ကွဲလွဲချက် = SS Residual / SS စုစုပေါင်း
• မရှင်းပြနိုင်သော ကွဲလွဲချက် = 5.9024 / 174.5
• မရှင်းပြနိုင်သော ကွဲလွဲချက် = 0.0338

ဤတန်ဖိုးကိုလည်း အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်နိုင်သည်။

• မရှင်းပြနိုင်သော ကွဲလွဲချက် = 1 – R ²
• မရှင်းပြနိုင်သော ကွဲလွဲချက် = 1 – 0.96617
• မရှင်းပြနိုင်သော ကွဲလွဲချက် = 0.0338

မော်ဒယ်၏ R-squared တန်ဖိုးသည် ခန့်မှန်းသူကိန်းရှင်ဖြင့် ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်၏ ကွဲလွဲမှုရာခိုင်နှုန်းကို ပြောပြသည်။

ထို့ကြောင့်၊ မရှင်းပြနိုင်သော ကွဲလွဲမှု နိမ့်လေ၊ တုံ့ပြန်မှု ကိန်းရှင်၏ ကွဲလွဲမှုကို ရှင်းပြရန် ခန့်မှန်းသူ ကိန်းရှင်များကို အသုံးပြု၍ မော်ဒယ်တစ်ခု စွမ်းဆောင်ရည် ပိုများလေဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

ကောင်းသော R-squared တန်ဖိုးဆိုသည်မှာ အဘယ်နည်း။
Excel တွင် R-squared တွက်ချက်နည်း
R ဖြင့် R-squared တွက်နည်း