လက်ဖြင့်ကျန်ရှိသောလမ်းကိုဖန်တီးနည်း

ကျန်ရှိသောကွက်ကွက် သည် x-ဝင်ရိုးတစ်လျှောက်နှင့် y-ဝင်ရိုးတစ်လျှောက် အကြွင်းအကျန် များ၏တန်ဖိုးများကို ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင် ခန့်မှန်းသူကိန်းရှင်၏တန်ဖိုးများကို ပြသသည့်ကွက်ကွက်အမျိုးအစားတစ်ခုဖြစ်သည်။

ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ ကျန်ရှိသော အစိတ်အပိုင်းများကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်း ရှိ၊ မရှိ အကဲဖြတ်ရန် ဤကြံစည်မှုကို အသုံးပြု သည်။

အောက်ဖော်ပြပါ အဆင့်ဆင့်သော ဥပမာသည် ဆုတ်ယုတ်မှုပုံစံအတွက် ကျန်နေသောကွက်ကွက်တစ်ခုကို ကိုယ်တိုင်ဖန်တီးနည်းကို ပြသထားသည်။

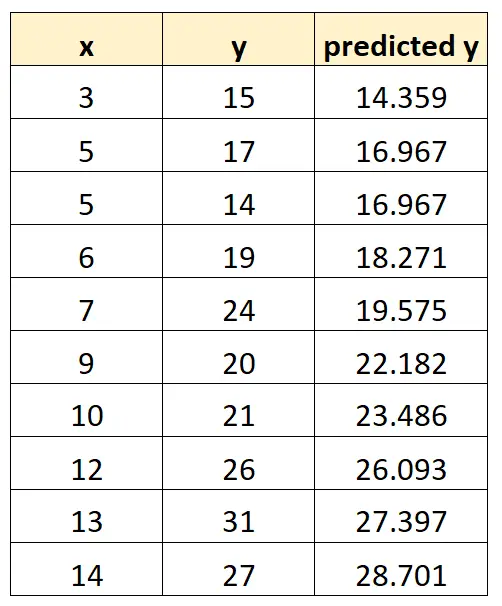
အဆင့် 1- ခန့်မှန်းတန်ဖိုးများကို ရှာပါ။

ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ ဒေတာအစုံနှင့် ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေလိုသည်ဆိုပါစို့။

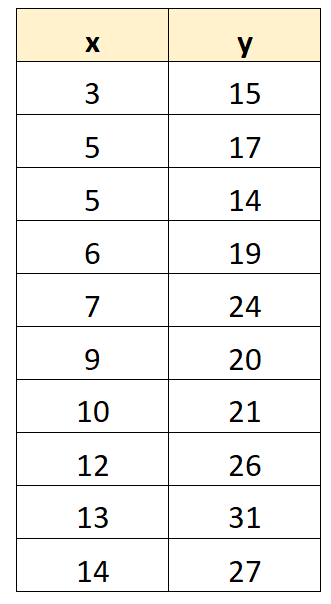
စာရင်းအင်းဆော့ဖ်ဝဲ (Excel၊ R၊ Python၊ SPSS စသည်ဖြင့်) ကို အသုံးပြု၍ တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံသည် အောက်ပါတို့ကို တွေ့ရှိနိုင်သည်-

y = 10.4486 + 1.3037(x)

ထို့နောက် x ၏တန်ဖိုးအပေါ်အခြေခံ၍ y တန်ဖိုးကို ခန့်မှန်းရန် ဤပုံစံကို အသုံးပြုနိုင်သည်။ ဥပမာ x = 3 ဆိုရင် y ဖြစ်မယ်လို့ ခန့်မှန်းတယ်။

y = 10.4486 + 1.3037(3) = 14.359

ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် ကြည့်ရှုမှု တစ်ခုစီအတွက် ဤလုပ်ငန်းစဉ်ကို ပြန်လုပ်နိုင်ပါသည်။

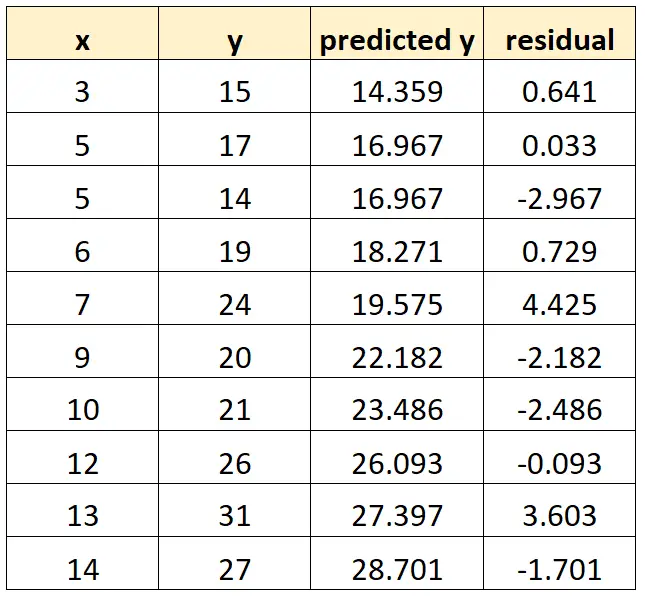
အဆင့် 2: အကြွင်းအကျန်များကိုရှာပါ။

ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် ပေးထားသည့် စောင့်ကြည့်မှုတစ်ခုအတွက် ကျန်နေသေးသည့်အရာအား အောက်ပါအတိုင်း တွက်ချက်သည်-

အကြွင်း = သတိပြုမိသောတန်ဖိုး – ခန့်မှန်းတန်ဖိုး

ဥပမာအားဖြင့်၊ ပထမရှုမြင်မှု၏ကျန်ကြွင်းအား အောက်ပါအတိုင်း တွက်ချက်ရမည်ဖြစ်ပါသည်။

လက်ကျန် = 15 – 14.359 = 0.641

ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် ကြည့်ရှုမှုတစ်ခုစီအတွက် ဤလုပ်ငန်းစဉ်ကို ပြန်လုပ်နိုင်ပါသည်။

အဆင့် 3: ကျန်ရှိသောကွက်ကွက်ကိုဖန်တီးပါ။

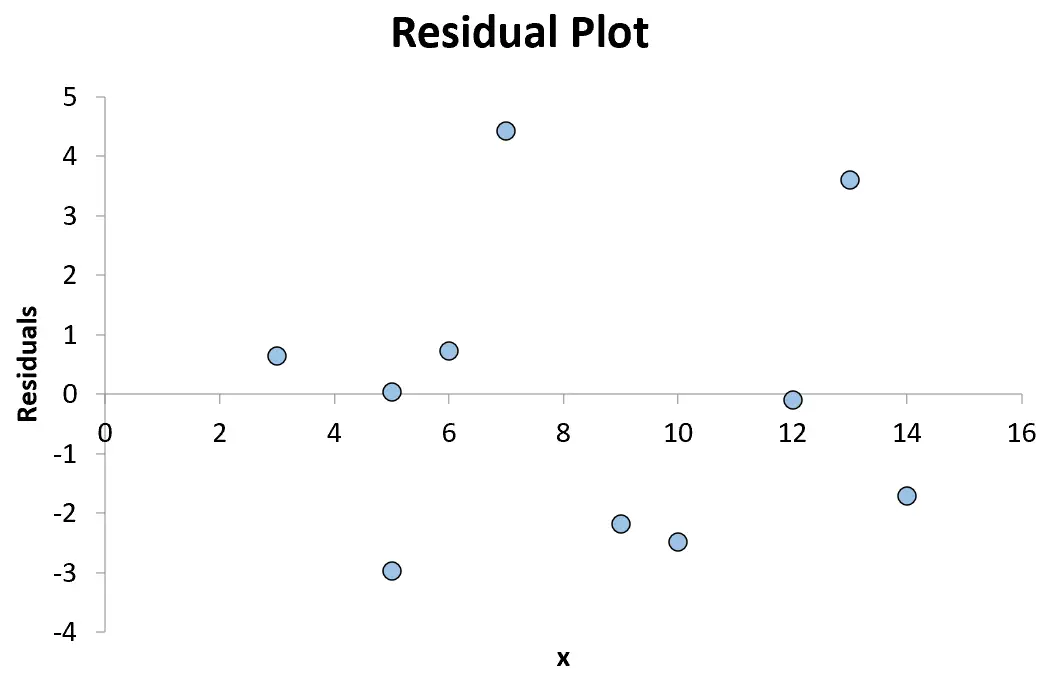
နောက်ဆုံးတွင်၊ x-ဝင်ရိုးတစ်လျှောက်နှင့် y-ဝင်ရိုးတစ်လျှောက် အကြွင်းအကျန်များကို x-တန်ဖိုးများထားခြင်းဖြင့် ကျန်ရှိသောကွက်ကွက်တစ်ခုကို ဖန်တီးနိုင်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ဂရပ်၌ ကျွန်ုပ်တို့ထည့်ရမည့် ပထမအချက်မှာ (၃၊ ၀.၆၄၁)၊

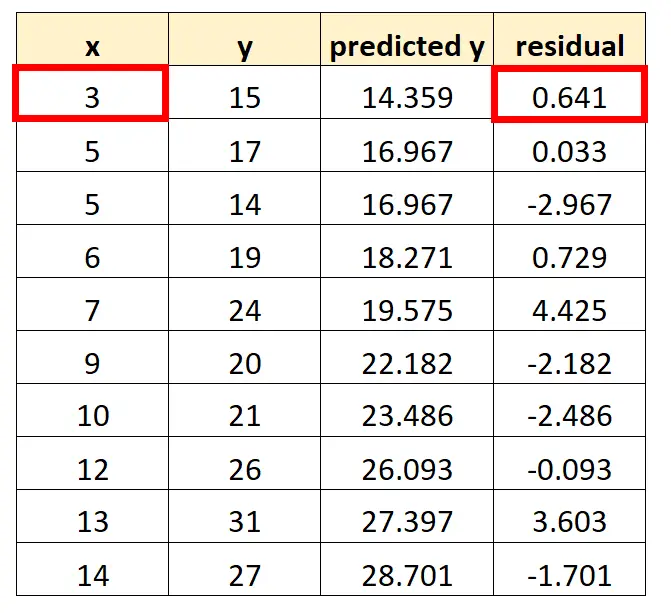
ကျွန်ုပ်တို့၏ဂရပ်တွင် ကျွန်ုပ်တို့ထည့်မည့် နောက်ထပ်အမှတ်မှာ (၅၊ ၀.၀၃၃)၊

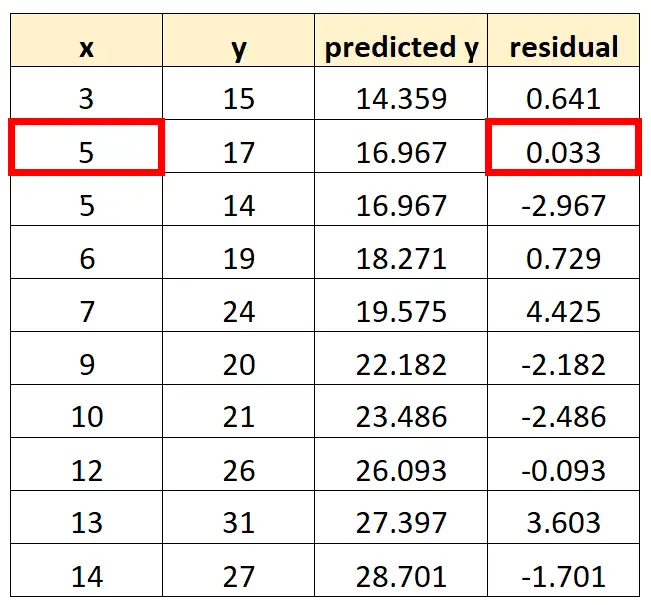
ကျွန်ုပ်တို့သည် ဇတ်ကွက်တွင် x-တန်ဖိုးများနှင့် ကျန်ရှိသော အတွဲ ၁၀ ခုလုံးကို တွဲလျက်ထားရှိသည်အထိ ကျွန်ုပ်တို့ ဆက်လက်လုပ်ဆောင်ပါမည်-

ဂရပ်ရှိ သုညအထက် အမှတ်သည် အပြုသဘောဆောင်သော အကြွင်းအကျန်ကို ကိုယ်စားပြုသည်။ ဆိုလိုသည်မှာ y အတွက် သတိပြုမိသောတန်ဖိုးသည် ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးထက် ကြီးနေခြင်းဖြစ်သည်။

သုညထက်နည်းသော မည်သည့်အမှတ်မဆို အနှုတ်ကျန်အကြွင်းကို ကိုယ်စားပြုသည်။ ဆိုလိုသည်မှာ y အတွက် သတိပြုမိသောတန်ဖိုးသည် ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးထက် နိမ့်နေခြင်းဖြစ်သည်။

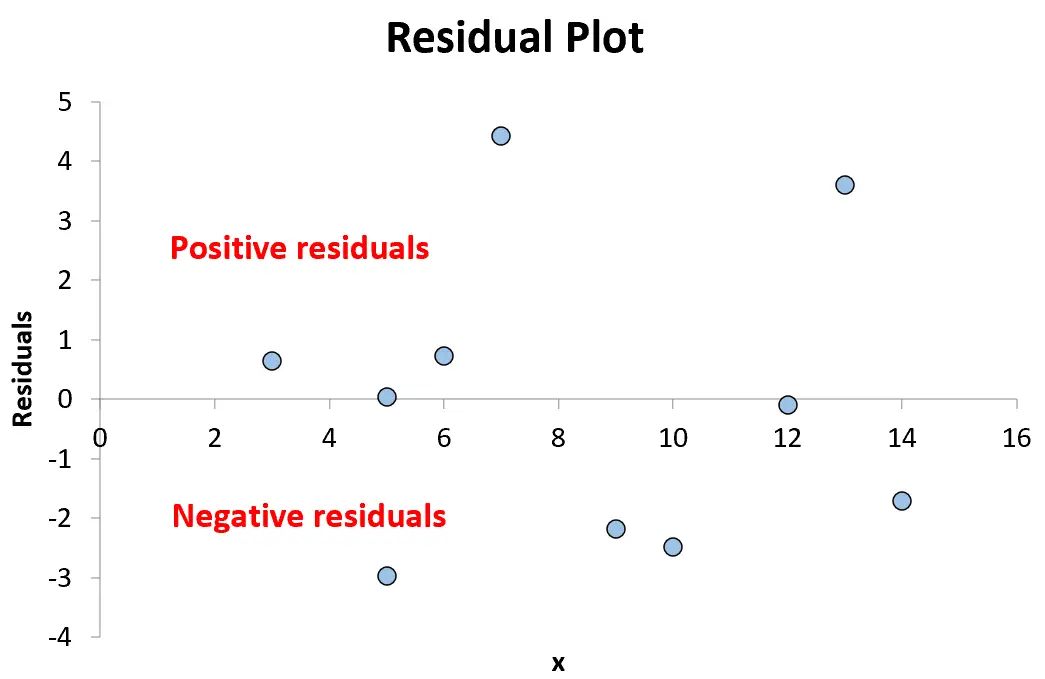
ဂရပ်ပေါ်ရှိ အမှတ်များသည် ရှင်းရှင်းလင်းလင်းမရှိသော 0 ၏ကျန်ရှိသောတစ်ဝိုက်တွင် ကျပန်းဖြန့်ကျဲထားသောကြောင့် x နှင့် y အကြားဆက်နွယ်မှုသည် linear ဖြစ်ပြီး linear regression model ကိုအသုံးပြုရန်သင့်လျော်ကြောင်းဖော်ပြသည်။

အကြွင်းအကျန်များသည် ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်များ တိုးလာသည်နှင့်အမျှ စနစ်တကျ တိုး သို့မဟုတ် လျော့မသွားသောကြောင့်၊ ဆိုလိုသည်မှာ heteroscedasticity သည် ဤဆုတ်ယုတ်မှုပုံစံအတွက် ပြဿနာမဟုတ်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော ကိန်းဂဏန်းဆော့ဖ်ဝဲကို အသုံးပြု၍ ကျန်ရှိသောကွက်ကွက်များကို ဖန်တီးနည်းကို ရှင်းပြသည်-

TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် ကျန်ရှိသော ဇာတ်ကွက်တစ်ခုကို ဖန်တီးနည်း
Excel တွင် Residual Plot ဖန်တီးနည်း
R တွင်ကျန်ရှိသောကွက်ကွက်ဖန်တီးနည်း
Python တွင် Residual Plot ဖန်တီးနည်း