တိုးပွားလာသော အကြိမ်ရေ

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် တိုးပွားလာသောအကြိမ်ရေကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ စုစည်းမှုကြိမ်နှုန်း၏ အဓိပ္ပါယ်၊ ဥပမာများဖြင့် တိုးပွားလာသော ကြိမ်နှုန်းကို မည်ကဲ့သို့ တွက်ချက်ရသနည်း၊ နောက်ဆုံးတွင် ရှိနေသည့် တိုးပွားလာသော ကြိမ်နှုန်းများ၏ အမျိုးအစားများကို လေ့လာပါမည်။

စုစည်းမှုကြိမ်နှုန်းဆိုတာဘာလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ စုဆောင်းမှုအကြိမ်ရေ သည် ကြိမ်နှုန်းများ၏ စုစည်းပေါင်းလဒ်ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ တန်ဖိုးတစ်ခု၏ တိုးပွားလာသော ကြိမ်နှုန်းသည် ထိုတန်ဖိုး၏ ကြိမ်နှုန်းနှင့် အောက်တန်ဖိုးများအားလုံး၏ ကြိမ်နှုန်းများနှင့် ညီမျှသည်။

စုစည်းမှု ကြိမ်နှုန်း နှစ်မျိုး ရှိသည်- စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း နှင့် စုစည်း နှိုင်းရ ကြိမ်နှုန်း။ စုစည်းမှု အကြိမ်ရေ အမျိုးအစား တစ်ခုစီကို မည်ကဲ့သို့ တွက်ချက်ထားသည်ကို အောက်တွင် ကြည့်ရှုပါမည်။

စာရင်းဇယားများတွင် တိုးပွားလာသော ကြိမ်နှုန်း၏ အဓိပ္ပါယ်ကို နားလည်ရန်၊ ကြိမ်နှုန်း၏ သဘောတရားကို ဦးစွာ ရှင်းရှင်းလင်းလင်း သိထားရပါမည်။ ထို့ကြောင့် ရှင်းလင်းချက်မပြမီ အောက်ပါပို့စ်ကို ဝင်ရောက်ကြည့်ရှုရန် အကြံပြုအပ်ပါသည်။

စုစည်းမှုအကြိမ်ရေကို ဘယ်လိုတွက်ရမလဲ

ကိန်းဂဏန်းနမူနာတစ်ခု၏ တိုးပွားလာသော ကြိမ်နှုန်းကို တွက်ချက် ရန် အဆင့်များမှာ-

1. အသေးဆုံးမှ အကြီးဆုံးမှ အကြီးဆုံးသို့ စီထားသော ဒေတာအစုံတွင် ပေါ်လာသည့် မတူညီသောတန်ဖိုးများပါသော ဇယားတစ်ခုကို ဖန်တီးပါ။
2. တန်ဖိုးတစ်ခုစီ၏ ပကတိအကြိမ်ရေကို ရှာပါ။
3. တန်ဖိုး၏ ကြိမ်နှုန်းနှင့် သေးငယ်သော တန်ဖိုးအားလုံး၏ ကြိမ်နှုန်းများကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်ထားသည့် တန်ဖိုးတစ်ခုစီ၏ တိုးပွားလာသော ကြိမ်နှုန်းကို ရှာပါ။

ထို့ကြောင့် တိုးပွားလာသော ကြိမ်နှုန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

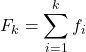
ရွှေ-

• 

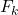
  တန်ဖိုး၏ တိုးပွားလာသော ကြိမ်နှုန်းဖြစ်သည်။

  

  .

• 

  တန်ဖိုး၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။

  

  .

ဤအဆင့်များသည် စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို တွက်ချက်ရန်အတွက် ဖြစ်သည်၊ သို့သော် တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းလည်း ရှိပါသည်။ အောက်တွင် စုဆောင်းထားသော ကြိမ်နှုန်း နှစ်မျိုးနှင့် အမျိုးအစား တစ်ခုစီကို တွေ့ရှိပုံတို့ အကြား ခြားနားချက်ကို ကျွန်ုပ်တို့ မြင်ရပါမည်။

တိုးပွားလာသော ကြိမ်နှုန်းအမျိုးအစားများ

ကိန်းဂဏန်းစာရင်းဇယားများတွင် စုစည်းမှုကြိမ်နှုန်း နှစ်မျိုးရှိသည်။

• စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း : ၎င်းသည် ပကတိ ကြိမ်နှုန်းများ ၏ စုစည်းမှု ပေါင်းလဒ် ဖြစ်သည်။
• တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း : ၎င်းသည် နှိုင်းရကြိမ်နှုန်း များ၏ စုစည်းပေါင်းလဒ်ဖြစ်သည်။

စုဆောင်းထားသော ကြိမ်နှုန်းအမျိုးအစားတစ်ခုစီ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် တစ်ခုချင်းစီကို မည်သို့ရယူပုံ၏ ဥပမာကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။

စုစည်းမှု ပကတိ အကြိမ်ရေ

စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း ကို F _i သင်္ကေတဖြင့် ကိုယ်စားပြုပြီး မေးခွန်းရှိ တန်ဖိုးထက် နည်းသော တန်ဖိုးများနှင့် ညီမျှသော ပကတိကြိမ်နှုန်းများကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်သည်။ ထို့နောက်၊ သင့်တွင် ကိန်းဂဏန်းအချက်အလက်အစုအဝေးတစ်ခု၏ ပကတိအကြိမ်ရေကို တွက်ချက်သည့် ခိုင်မာသောဥပမာတစ်ခုရှိသည်။

• ကျောင်းသား 30 ရှိသော အတန်းတစ်တန်းတွင် စာရင်းအင်းဘာသာရပ်တွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။ မှတ်စုတစ်ခုစီ၏ ပကတိအကြွင်းမဲ့ ကြိမ်နှုန်းသည် အဘယ်နည်း။

ဂဏန်းများအားလုံးသည် ကိန်းပြည့်များသာဖြစ်နိုင်သောကြောင့် ၎င်းသည် သီးခြားကွဲလွဲချက်ဖြစ်သည်။ ထို့ကြောင့် အချက်အလက်များကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ရန် မလိုအပ်ပါ။

ထို့ကြောင့်၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို ဆုံးဖြတ်ရန်၊ ကိန်းဂဏန်းနမူနာတွင် တန်ဖိုးတစ်ခုစီတွင် ပေါ်လာသည့် အကြိမ်အရေအတွက်ဖြစ်သည့် တန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ဦးစွာရှာဖွေရပါမည်။

ယခု ကျွန်ုပ်တို့သည် တန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို သိရှိပြီး၊ ကျွန်ုပ်တို့သည် ၎င်းတို့၏ တိုးပွားလာသော ပကတိကြိမ်နှုန်းများကို တွက်ချက်နိုင်ပါသည်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်- ကျွန်ုပ်တို့သည် တန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် အသေးငယ်ဆုံးတန်ဖိုးများ၏ ပကတိကြိမ်နှုန်းအားလုံးကို ပေါင်းထည့်ခြင်း သို့မဟုတ် ဆန့်ကျင်ဘက်အနေနှင့်၊ ကျွန်ုပ်တို့သည် တန်ဖိုး၏ absolute frequency နှင့် ယခင်တန်ဖိုးများ၏ ပကတိအကြိမ်ရေကို ပေါင်းထည့်သည် . တန်ဖိုး။

အတိုချုပ်အားဖြင့်၊ လေ့ကျင့်ခန်း၏ ပကတိ တိုးပွားလာသော အကြိမ်ရေနှင့် ဇယားမှာ အောက်ပါအတိုင်း ဖြစ်သည်။

နောက်ဆုံးတန်ဖိုး၏ စုဆောင်းထားသော ပကတိကြိမ်နှုန်းသည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် အမြဲတိုက်ဆိုင်နေကြောင်း သတိပြုပါ။ မဟုတ်ပါက သင်သည် တွက်ချက်မှုတွင် မှားယွင်းသွားသည်ဟု ဆိုလိုသည်။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း ကို H _i သင်္ကေတဖြင့် ကိုယ်စားပြုပြီး မေးခွန်းရှိတန်ဖိုးထက် နည်းသော တန်ဖိုးများ ဆွေမျိုးကြိမ်နှုန်းများကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်သည်။ အောက်တွင် စုစည်းမှု နှိုင်းရကြိမ်နှုန်းကို ဆုံးဖြတ်သည့် ယခင်ပြဿနာနှင့် တူညီသော ဒေတာဖြင့် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကို သင်တွေ့မြင်နိုင်ပါသည်။

• အတန်းတစ်တန်းတွင် ကျောင်းသား အယောက် ၃၀ ၏ စာရင်းဇယားတွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်း ဖြစ်သည်။ မှတ်စုတစ်ခုစီ၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းသည် အဘယ်နည်း။

ဤကိစ္စတွင်၊ ကိန်းရှင်သည် ဒဿမတန်ဖိုးကိုမယူနိုင်သောကြောင့် ကွဲပြားသည်။ ထို့ကြောင့် ဒေတာများကို ကြားကာလအလိုက် အုပ်စုဖွဲ့ရန် မလိုအပ်သော်လည်း တွက်ချက်မှုများကို တိုက်ရိုက်လုပ်ဆောင်နိုင်ပါသည်။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ကြိမ်နှုန်းဇယားကိုရေးဆွဲပြီး မတူညီသောတန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ဆုံးဖြတ်သည်-

ထို့နောက်၊ ကျွန်ုပ်တို့သည် အကြွင်းမဲ့ ကြိမ်နှုန်းကို လေ့လာသုံးသပ်မှု အရေအတွက် (၃၀) ဖြင့် ပိုင်းခြား၍ ဆုံးဖြတ်သည့် တန်ဖိုးတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်ပါသည်။

ပြီးတော့ dataset ရဲ့ absolute frequency နဲ့ relative frequency ကို တွက်ချက်ပြီးတာနဲ့၊ cumulative relative frequency ကို ရနိုင်ပါတယ်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ သင်သည် မေးခွန်းရှိတန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်းနှင့် ယခင်နှိုင်းရကြိမ်နှုန်းများအားလုံးကို ပေါင်းထည့်ရမည်ဖြစ်ပြီး၊ သို့မဟုတ် တူညီသောပမာဏဖြစ်သည့် ယခင်စုဆောင်းထားသော ဆွေမျိုးကြိမ်နှုန်းကို ပေါင်းထည့်ရမည်-

အတိုချုပ်အားဖြင့်၊ absolute frequency၊ relative frequency နှင့် cumulative relative frequency ပါသော ကြိမ်နှုန်းဇယားမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း၏ နောက်ဆုံးတန်ဖိုးသည် အမြဲတမ်း 1 ဖြစ်သင့်သည်။ အခြားနံပါတ်ရပါက၊ တွက်ချက်မှုတွင် သင်သည် မှားယွင်းသွားသည်ဟု ဆိုလိုသည်။