ဘီတာ ဖြန့်ဝေခြင်း။
ဤဆောင်းပါးတွင် ဘီတာဖြန့်ချီခြင်းမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ အလားတူ၊ ဘီတာဖြန့်ချီရေးဂရပ်နှင့် ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကို သင်မြင်နိုင်မည်ဖြစ်သည်။
ဘီတာ ဖြန့်ဖြူးမှုကား အဘယ်နည်း။
ဘီတာ ဖြန့်ဝေမှုသည် ကြားကာလ (0,1) တွင် သတ်မှတ်ထားသော ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုဖြစ်ပြီး အပြုသဘောဆောင်သော ဘောင်နှစ်ခု- α နှင့် β ဖြင့် ကန့်သတ်ချက်များ ပြုလုပ်ထားသည်။ တစ်နည်းဆိုရသော် ဘီတာဖြန့်ဖြူးမှုတန်ဖိုးများသည် α နှင့် β ဘောင်များပေါ်တွင် မူတည်သည်။
ထို့ကြောင့်၊ ဘီတာဖြန့်ဖြူးမှု၏ အဓိကအင်္ဂါရပ်မှာ ၎င်း၏ပုံသဏ္ဍာန်ကို α နှင့် β ဘောင်များဖြင့် ထိန်းချုပ်နိုင်ခြင်းဖြစ်သည်။ ထို့အပြင်၊ ဘီတာဖြန့်ဝေမှုကို 0 နှင့် 1 အကြား တန်ဖိုးရှိသော ကျပန်းပြောင်းလွဲချက်များကို သတ်မှတ်ရန် အသုံးပြုသည်။
စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲခြင်းကို ဘီတာဖြန့်ဝေမှုဖြင့် ထိန်းချုပ်ထားကြောင်း ညွှန်ပြရန် မှတ်သားစရာများစွာရှိသည်၊ အဖြစ်အများဆုံးမှာ-
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ee1d0d8a1624a017b8ef9ce8a67c694e_l3.png)
စာရင်းဇယားများတွင်၊ ဘီတာဖြန့်ဖြူးမှုတွင် အလွန်ကွဲပြားသော အပလီကေးရှင်းများရှိသည်။ ဥပမာအားဖြင့်၊ မတူညီသောနမူနာများတွင် ရာခိုင်နှုန်းကွဲပြားမှုများကို လေ့လာရန် ဘီတာဖြန့်ဝေမှုကို အသုံးပြုသည်။ အလားတူ၊ ပရောဂျက်စီမံခန့်ခွဲမှုတွင် Pert ခွဲခြမ်းစိတ်ဖြာမှုလုပ်ဆောင်ရန် ဘီတာဖြန့်ဝေမှုကို အသုံးပြုသည်။
ဘီတာဖြန့်ချီရေး ကြံစည်မှု
ဘီတာဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် ဘီတာဖြန့်ဝေမှု၏ သိပ်သည်းဆနှင့် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို အောက်တွင် ပုံဖော်ထားသည်။
အောက်တွင် ဘီတာဖြန့်ဝေမှု၏ သိပ်သည်းဆလုပ်ဆောင်ပုံဂရပ်သည် α နှင့် β ဘောင်များပေါ်မူတည်၍ ကွဲပြားသည်ကို သင်မြင်နိုင်သည်။
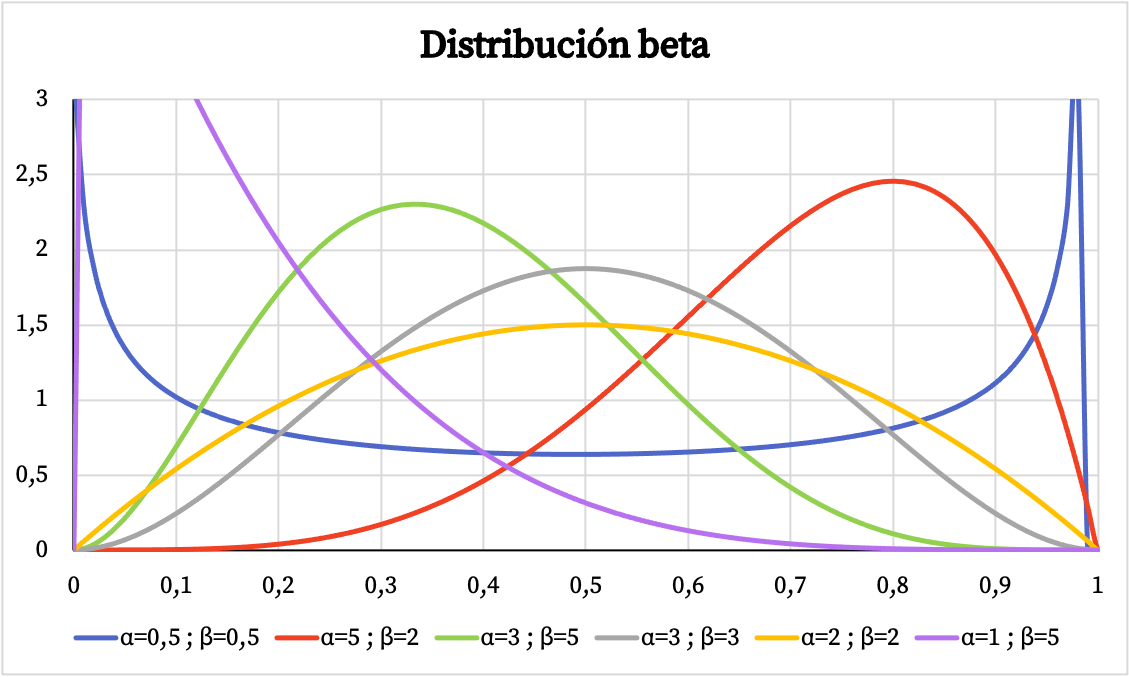
အလားတူ၊ အောက်တွင် ပါရာမီတာများ α နှင့် β တို့ကို အခြေခံ၍ ဘီတာဖြန့်ဖြူးခြင်း၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေ၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုကို သင်တွေ့မြင်နိုင်ပါသည်။
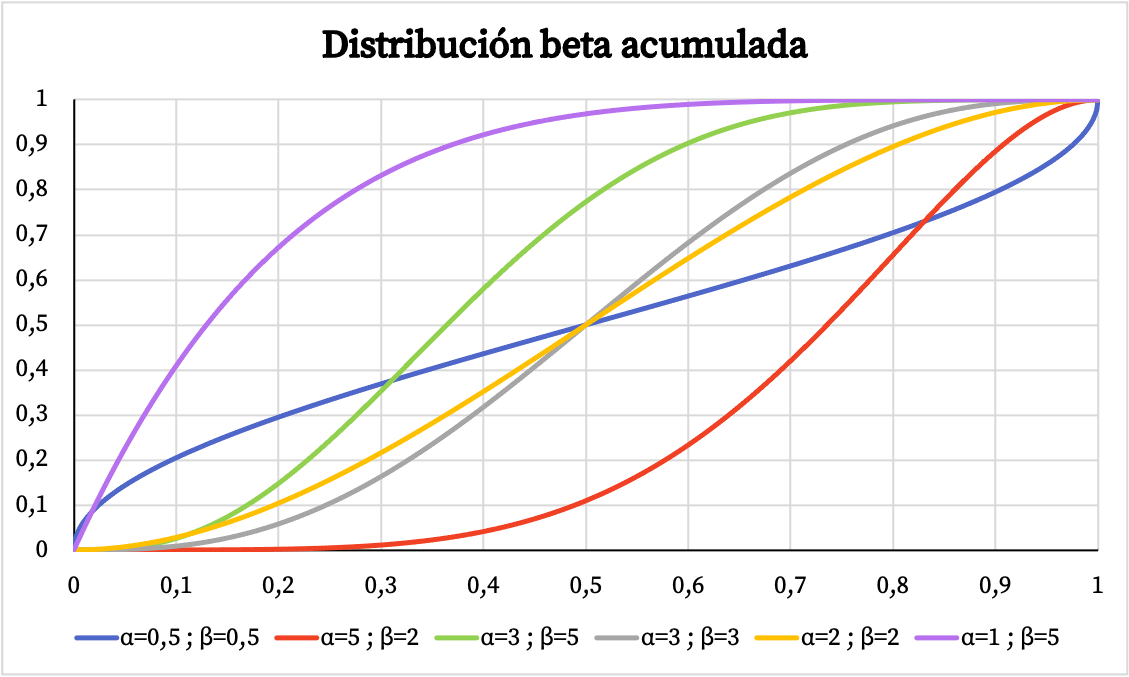
ဘီတာ ဖြန့်ဖြူးခြင်း၏ လက္ခဏာများ
ဤကဏ္ဍတွင် ဘီတာဖြန့်ချီခြင်း၏ အရေးကြီးဆုံးဝိသေသလက္ခဏာများကို ကျွန်ုပ်တို့ကြည့်ရှုပါမည်။
- beta ဖြန့်ဖြူးမှု၏ α နှင့် β ဘောင်များသည် အစစ်အမှန်နှင့် အပြုသဘောဆောင်သော ဂဏန်းများဖြစ်သည်။
![\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=” Rendered by QuickLaTeX.com” height=” 54″ width=” 44″ style=” vertical-align: 0px;” ></p>
</p>
<ul>
<li> ဘီတာ ဖြန့်ဖြူးမှု၏ ဒိုမိန်းသည် 0 မှ 1 အထိ ကွဲပြားသည်၊ အစွန်းနှစ်ခု မပါဝင်ပါ။</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-442bebaba847543d6db71cdf0127a4b0_l3.png)
![]()
- ဘီတာ ဖြန့်ဖြူးမှု၏ ပျမ်းမျှ သည် အယ်လ်ဖာ အပေါင်း ဘီတာ ဖြင့် ပိုင်းခြားထားသော အယ်လ်ဖာ နှင့် ညီမျှသည်။
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4530a8b72211111e8bec79b6388e00a7_l3.png)
- ဘီတာဖြန့်ဝေမှု၏ကွဲလွဲမှုကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်နိုင်သည်-
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-71c6ef40db833722e63c56cd763d6601_l3.png)
- 1 ထက်ကြီးသော alpha နှင့် beta တန်ဖိုးများအတွက်၊ beta distribution mode ကို အောက်ပါအသုံးအနှုန်းများဖြင့် အလွယ်တကူ ရှာတွေ့နိုင်သည်-
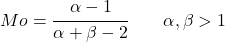
![]()
B(α,β) သည် beta လုပ်ဆောင်ချက်ဖြစ်ပြီး၊ ၎င်းသည် အောက်ပါအတိုင်း သတ်မှတ်သည်။
![]()
- ဘီတာ ဖြန့်ဝေမှု၏ စုစည်းဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်မှာ-
![]()
B(x;α,β) သည် မပြည့်စုံသော beta လုပ်ဆောင်ချက်ဖြစ်ပြီး၊ သတ်မှတ်ထားသောနေရာတွင်၊
![]()
- X သည် ဘီတာဖြန့်ဖြူးမှုမှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်ပါက၊ 1-X သည် ဘီတာဖြန့်ဝေမှုတစ်ခုမှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်ပြီး အယ်လ်ဖာနှင့်ဘီတာကန့်သတ်ချက်များသည် မူလဘီတာဖြန့်ဝေမှု၏ ဘီတာနှင့် အယ်လ်ဖာဘောင်များ အသီးသီးဖြစ်သည်။
![]()
- ဘီတာ ဖြန့်ဖြူးမှု၏ အယ်လ်ဖာနှင့် ဘီတာ ဘောင်များသည် 1 နှင့် ညီမျှပါက၊ ဖြန့်ဝေမှုသည် ကန့်သတ်ဘောင် 0 နှင့် 1 တို့၏ တစ်ပြေးညီ ဖြန့်ဖြူးမှုနှင့် ညီမျှသည်။
![]()