Mae vs. rmse- ဘယ် metric ကို သုံးသင့်သလဲ။

ဆုတ်ယုတ်မှုပုံစံများကို တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် တစ်ခုအကြား ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန်အတွက် အသုံးပြုသည်။

ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို အံဝင်ခွင်ကျဖြစ်စေသည့်အခါတိုင်း၊ တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးကို ခန့်မှန်းရန် တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးများကို ခန့်မှန်းရန်အတွက် မော်ဒယ်သည် ခန့်မှန်းသူကိန်းရှင်များ၏ တန်ဖိုးများကို မည်မျှကောင်းစွာအသုံးပြုနိုင်သည်ကို ကျွန်ုပ်တို့နားလည်လိုပါသည်။

အောက်ပါအတိုင်း တွက်ချက်ထားသည့် မော်ဒယ်တစ်ခုသည် ဒေတာအစုံနှင့် ကိုက်ညီမှု မည်မျှ ကောင်းမွန်ကြောင်း တိုင်းတာရန် ကျွန်ုပ်တို့ အသုံးပြုလေ့ရှိသည့် မက်ထရစ်နှစ်ခုမှာ ပျမ်းမျှ အကြွင်းမဲ့ အမှား (MAE) နှင့် အောက်ပါအတိုင်း တွက်ချက်ထားသည့် အရင်းအနှီးစတုရန်းအမှား (RMSE) ဖြစ်သည်။

MAE : ဒေတာအတွဲတစ်ခုရှိ ခန့်မှန်းတန်ဖိုးများနှင့် အမှန်တကယ်တန်ဖိုးများအကြား ပျမ်းမျှအကြွင်းမဲ့ကွာခြားချက်ကို ပြောပြသော မက်ထရစ်တစ်ခု။ MAE နိမ့်လေ၊ မော်ဒယ်တစ်ခုသည် ဒေတာအစုံနှင့် လိုက်ဖက်လေဖြစ်သည်။

MAE = 1/n * Σ|y _i – ŷ _i |

ရွှေ-

• ∑ သည် “ပေါင်း” ဟူသော သင်္ကေတတစ်ခုဖြစ်သည်။
• y _i သည် ^ith observation အတွက် မှတ်သားထားသောတန်ဖိုးဖြစ်သည်။
• ŷ _i သည် i ^th observation အတွက် ခန့်မှန်းတန်ဖိုးဖြစ်သည်။
• n သည် နမူနာအရွယ်အစားဖြစ်သည်။

RMSE : ခန့်မှန်းတန်ဖိုးများနှင့် ဒေတာအတွဲတစ်ခုရှိ အမှန်တကယ်တန်ဖိုးများကြားတွင် ခန့်မှန်းတန်ဖိုးများနှင့် ကိန်းဂဏန်းများအကြား နှစ်ထပ်ကိန်းအမြစ်၏ နှစ်ထပ်ကိန်းကို ပြောပြသော မက်ထရစ်တစ်ခု။ RMSE နိမ့်လေ၊ မော်ဒယ်တစ်ခုသည် ဒေတာအစုံနှင့် ကိုက်ညီလေလေဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

RMSE = √ Σ(y _i – ŷ _i ) ² / n

ရွှေ-

• ∑ သည် “ပေါင်း” ဟူသော သင်္ကေတတစ်ခုဖြစ်သည်။
• ŷ _i သည် i ^th observation အတွက် ခန့်မှန်းတန်ဖိုးဖြစ်သည်။
• y _i သည် ^ith observation အတွက် မှတ်သားထားသောတန်ဖိုးဖြစ်သည်။
• n သည် နမူနာအရွယ်အစားဖြစ်သည်။

ဥပမာ- RMSE နှင့် MAE တွက်ချက်ခြင်း။

ဘတ်စကတ်ဘောဂိမ်းတစ်ခုတွင် ကစားသမား 10 ဂိုးသွင်းမည်ကို ခန့်မှန်းရန် ဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့အသုံးပြုသည်ဆိုပါစို့။

အောက်ဖော်ပြပါဇယားသည် ကစားသမားများမှ ရရှိသည့်အမှန်တကယ်ရမှတ်များနှင့် မော်ဒယ်မှ ခန့်မှန်းထားသော အမှတ်များကို ပြသသည်-

MAE ဂဏန်းတွက်စက်ကို အသုံးပြု၍ MAE သည် 3.2 ဖြစ်ကြောင်း တွက်ချက်နိုင်ပါသည်။

၎င်းသည် မော်ဒယ်မှ ခန့်မှန်းထားသော တန်ဖိုးများနှင့် အမှန်တကယ်တန်ဖိုးများအကြား ပျမ်းမျှအကြွင်းမဲ့ ကွာခြားချက်မှာ 3.2 ဖြစ်သည်။

RMSE ဂဏန်းတွက်စက် ကို အသုံးပြု၍ RMSE သည် 4 နှင့် ညီမျှကြောင်း တွက်ချက်နိုင်ပါသည်။

၎င်းသည် ခန့်မှန်းထားသော ရမှတ်များနှင့် အမှန်တကယ်ရမှတ်များအကြား လေးထပ်ကိန်း၏ နှစ်ထပ်ကိန်းကို ဆိုလိုသည်မှာ နှစ်ထပ်ကိန်း ကွာခြားချက်မှာ 4 ဖြစ်သည်။

မက်ထရစ်တစ်ခုစီသည် မော်ဒယ်မှပြုလုပ်သော ခန့်မှန်းတန်ဖိုးနှင့် ဒေတာအတွဲရှိ အမှန်တကယ်တန်ဖိုးကြား ပုံမှန်ကွာခြားချက်ကို အကြံဉာဏ်ပေးသည်ကို သတိပြုပါ၊ သို့သော် မက်ထရစ်တစ်ခုစီ၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်မှာ အနည်းငယ်ကွဲပြားပါသည်။

RMSE နှင့် MAE- မည်သည့် Metric ကို သုံးသင့်သနည်း။

အကယ်၍ သင်သည် ပျမ်းမျှမှ ဝေးကွာသော မှတ်သားမှုများကို အလေးချိန်ပို၍ သတ်မှတ်လိုပါက (ဆိုလိုသည်မှာ 20 ၏ သွေဖည်မှု သည် 10 ၏ သွေဖည်မှုထက် နှစ်ဆပိုဆိုးသည်)၊ RMSE သည် အမှားအယွင်းကို တိုင်းတာရန် RMSE ကို အသုံးပြုခြင်းသည် ပိုကောင်းသည်၊ ဆိုလိုရင်းမှ ဝေးကွာသော ရှုမြင်ချက်များကို ပို၍ ထိလွယ်ရှလွယ်သည်။

သို့သော်၊ 20 တွင် “ offset” သည် 10 တွင် “ offset” ဖြစ်ခြင်းထက်နှစ်ဆပိုဆိုးပါက MAE ကိုအသုံးပြုခြင်းသည်ပိုမိုကောင်းမွန်သည်။

ယင်းကို သရုပ်ဖော်ရန်၊ ကျွန်ုပ်တို့တွင် ရမှတ်အရေအတွက်အရ ရှင်းရှင်းလင်းလင်း သာလွန်သော ကစားသမားတစ်ဦးရှိသည် ဆိုပါစို့။

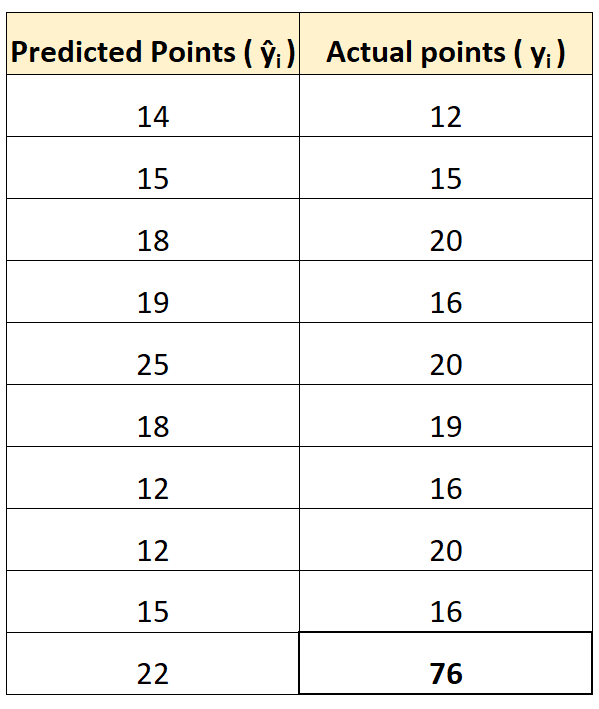
အစောပိုင်းတွင်ဖော်ပြထားသောအွန်လိုင်းဂဏန်းတွက်စက်များကိုအသုံးပြု၍ MAE နှင့် RMSE တို့ကိုတွက်ချက်နိုင်သည်-

• MAE : ၈
• RMSE : 16.4356

RMSE သည် MAE ထက်များစွာတိုးကြောင်းသတိပြုပါ။

အကြောင်းမှာ RMSE သည် ၎င်း၏ဖော်မြူလာတွင် နှစ်ထပ်ကိန်းကွဲလွဲချက်များကို အသုံးပြုပြီး 76 နှင့် 22 ခန့်မှန်းတန်ဖိုးကြား နှစ်ထပ်ကိန်းခြားနားချက်သည် အလွန်ကြီးမားသောကြောင့်ဖြစ်သည်။ ၎င်းသည် RMSE တန်ဖိုးကို သိသာထင်ရှားစွာ မြင့်တက်လာစေသည်။

လက်တွေ့တွင်၊ ကျွန်ုပ်တို့သည် ပုံမှန်အားဖြင့် များစွာသော ဆုတ်ယုတ်မှုပုံစံများကို ဒေတာအတွဲတစ်ခုတွင် တပ်ဆင်ပြီး မော်ဒယ်တစ်ခုစီအတွက် ဤမက်ထရစ်များထဲမှ တစ်ခုကိုသာ တွက်ချက်ပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် မတူညီသော ဆုတ်ယုတ်မှုပုံစံသုံးမျိုးနှင့် ကိုက်ညီပြီး မော်ဒယ်တစ်ခုစီအတွက် RMSE ကို တွက်ချက်နိုင်သည်။ ထို့နောက် ကျွန်ုပ်တို့သည် အနိမ့်ဆုံး RMSE တန်ဖိုးရှိသော မော်ဒယ်ကို “ အကောင်းဆုံး” မော်ဒယ်အဖြစ် ရွေးချယ်မည်ဖြစ်သောကြောင့်၊ ၎င်းသည် ဒေတာအတွဲရှိ အမှန်တကယ်တန်ဖိုးများနှင့် ခန့်မှန်းချက်များကို အနီးစပ်ဆုံးပြုလုပ်ပေးသောကြောင့် ဖြစ်ပါသည်။

မည်သည့်အခြေအနေမျိုးတွင်မဆို၊ မော်ဒယ်တစ်ခုစီအတွက် တူညီသောမက်ထရစ်ကို သေချာတွက်ချက်ပါ။ ဥပမာအားဖြင့်၊ မော်ဒယ်တစ်ခုအတွက် MAE နှင့် အခြားမော်ဒယ်တစ်ခုအတွက် RMSE ကို မတွက်ချက်ပါနှင့်၊ ထို့နောက် ဤအတိုင်းအတာနှစ်ခုကို နှိုင်းယှဉ်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲကို အသုံးပြု၍ MAE တွက်ချက်နည်းကို ရှင်းပြသည်-

Excel တွင် Mean Absolute Error တွက်ချက်နည်း
R တွင် ဆိုလိုသည့် absolute error တွက်ချက်နည်း
Python တွင် Mean Absolute Error တွက်ချက်နည်း

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲကို အသုံးပြု၍ RMSE တွက်ချက်နည်းကို ရှင်းပြသည်-

Excel တွင် Mean Square Error တွက်ချက်နည်း
R တွင် အဓိပ္ပာယ် နှစ်ထပ် အမှားကို တွက်နည်း
Python တွင် Mean Squared Error ကို တွက်ချက်နည်း