Linear regression တွင် t-test ကို နားလည်ခြင်း။
Linear regression ကို ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန်အတွက် အသုံးပြုသည်။
ကျွန်ုပ်တို့သည် linear regression ကိုလုပ်ဆောင်သည့်အခါတိုင်း၊ ခန့်မှန်းသူ variable နှင့် response variable အကြား ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ဆက်နွယ်မှုရှိမရှိ သိလိုပါသည်။
regression slope အတွက် t-test ကို လုပ်ဆောင်ခြင်းဖြင့် အရေးပါမှုကို ကျွန်ုပ်တို့ စမ်းသပ်ပါသည်။ ဤ t-test အတွက် ကျွန်ုပ်တို့သည် အောက်ပါ null နှင့် အခြား သီအိုရီကို အသုံးပြုသည်-
- H 0 : β 1 = 0 (လျှောစောက်သည် သုညနှင့် ညီသည်)
- H A : β 1 ≠ 0 (လျှောစောက်သည် သုညနှင့် မညီပါ)
ထို့နောက် စမ်းသပ်စာရင်းအင်းကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။
t = b / SE b
ရွှေ-
- b : coefficient ၏ ခန့်မှန်းချက်
- SE b : ကိန်းဂဏန်းခန့်မှန်းချက်၏ စံအမှား
t နှင့် သက်ဆိုင်သော p-value သည် သတ်မှတ်ထားသော အတိုင်းအတာတစ်ခုအောက်၌ ရှိနေပါက (ဥပမာ α = 0.05)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်ပြီး ခန့်မှန်းသူ variable နှင့် response variable အကြား ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ဆက်နွယ်မှုရှိကြောင်း ကောက်ချက်ချပါသည်။
အောက်ပါဥပမာသည် လက်တွေ့တွင် linear regression model အတွက် t-test ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။
ဥပမာ- linear regression အတွက် t-test ကို လုပ်ဆောင်ခြင်း။
ပါမောက္ခတစ်ဦးသည် ၎င်း၏ကျောင်းသား ၄၀ အတွက် စာသင်ချိန်နှင့် စာမေးပွဲအဆင့်များကြား ဆက်စပ်မှုကို ခွဲခြမ်းစိတ်ဖြာလိုသည်ဆိုပါစို့။
၎င်းသည် ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် လက်ခံရရှိသော စာမေးပွဲရမှတ်များအဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်သည်။
အောက်ပါဇယားသည် ဆုတ်ယုတ်မှုပုံစံ၏ ရလဒ်များကို ပြသသည်-
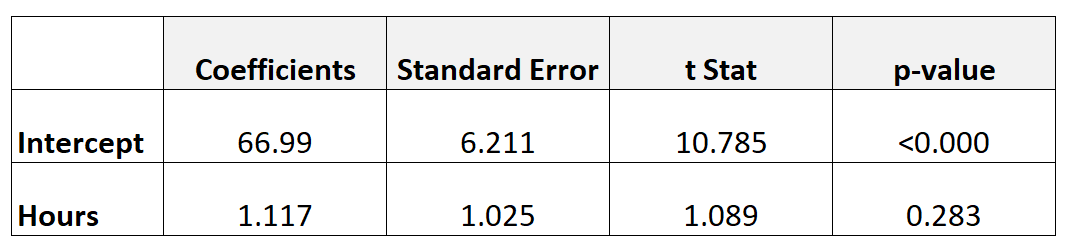
သင်ကြားသည့်နာရီများသည် နောက်ဆုံးစာမေးပွဲအဆင့်နှင့် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ဆက်စပ်မှုရှိမရှိ ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် t-test ကို လုပ်ဆောင်နိုင်ပါသည်။
ဤ t-test အတွက် ကျွန်ုပ်တို့သည် အောက်ပါ null နှင့် အခြား သီအိုရီကို အသုံးပြုသည်-
- H 0 : β 1 = 0 (လေ့လာခဲ့သော နာရီများ၏ လျှောစောက်သည် သုညနှင့် ညီမျှသည်)
- H A : β 1 ≠ 0 (လေ့လာထားသော နာရီများ၏ လျှောစောက်သည် သုညနှင့် ညီမျှသည်မဟုတ်ပါ)
ထို့နောက် စမ်းသပ်စာရင်းအင်းကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။
- t = b / SE b
- t = 1.117 / 1.025
- t = 1.089
df=n-2=40–2=38 နှင့် t = 1.089 နှင့် သက်ဆိုင်သော p-တန်ဖိုးသည် 0.283 ဖြစ်သည်။
ဤ p တန်ဖိုးကိုတွက်ချက်ရန် ကျွန်ုပ်တို့သည် T ရမှတ်မှ P တန်ဖိုးဂဏန်းတွက်စက် ကိုလည်း အသုံးပြုနိုင်ကြောင်း သတိပြုပါ။

ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။
ဆိုလိုသည်မှာ လေ့လာမှုနာရီများသည် နောက်ဆုံးစာမေးပွဲရလဒ်များကြားတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်စပ်မှု မရှိပါ ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် linear regression နှင့်ပတ်သက်သော နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-
Simple Linear Regression နိဒါန်း
Multiple Linear Regression အကြောင်း နိဒါန်း
regression coefficient ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။
ဆုတ်ယုတ်မှုတွင် အလုံးစုံအရေးပါမှုအတွက် F စစ်ဆေးမှုအား မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုမည်နည်း။