ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးခြင်းအကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ပုံမှန်ဖြန့်ဝေမှု၏ ဂုဏ်သတ္တိများနှင့် ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂရပ်များကို သင်တွေ့ရှိနိုင်မည်ဖြစ်သည်။

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

လော့ဂရစ်သမ်သည် ပုံမှန်ဖြ န့်ဝေမှု နောက်ဆက်တွဲဖြစ်သော ကျပန်းကိန်းရှင်တစ်ခုကို သတ်မှတ်ပေးသည့် လော့ဂရစ်သမ်ဖြင့် ပုံမှန်ဖြန့်ဝေမှုဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

ထို့ကြောင့်၊ variable X တွင် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုရှိလျှင် exponential function e ^x တွင် lognormal distribution တစ်ခုရှိသည်။

$X\sim \text{Lognormal}(\mu,\sigma^2)$

လော့ဂရစ်သမ်သည် အပြုသဘောဆောင်သည့် အငြင်းအခုံတစ်ခုသာယူသည့် လုပ်ဆောင်ချက်တစ်ခုဖြစ်သောကြောင့် ကိန်းရှင်တန်ဖိုးများသည် အပြုသဘောဆောင်သည့်အချိန်တွင်သာ လော့ဂ်ပုံမှန်ဖြန့်ဝေမှုကို အသုံးပြုနိုင်မည်ဖြစ်သည်။

စာရင်းဇယားများတွင် ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှု၏ မတူညီသောအသုံးချပရိုဂရမ်များကြားတွင်၊ ကျွန်ုပ်တို့သည် ငွေကြေးရင်းနှီးမြှုပ်နှံမှုများကို ပိုင်းခြားစိတ်ဖြာရန်နှင့် ယုံကြည်စိတ်ချရမှုဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာမှုများကို လုပ်ဆောင်ရန် ဤဖြန့်ဖြူးမှုအသုံးပြုမှုကို ပိုင်းခြားထားပါသည်။

lognormal ဖြန့်ဝေခြင်းကို Tinaut ဖြန့်ဖြူးမှုဟုလည်း ခေါ်ကြပြီး၊ တစ်ခါတစ်ရံတွင် lognormal distribution သို့မဟုတ် log-normal distribution အဖြစ်လည်း ရေးသားကြသည်။

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှု ဇာတ်ကွက်

ယခု ကျွန်ုပ်တို့သည် lognormal ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ကို သိပြီးသောအခါ၊ လော့ဂ်နမာဖြန့်ဝေမှု၏ ဂရပ်ဖစ်ကိုယ်စားပြုပုံသည် ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှတန်ဖိုးများနှင့် ၎င်း၏စံသွေဖည်မှုအပေါ် မူတည်၍ မည်သို့ကွဲပြားသည်ကို ဤအပိုင်းတွင် တွေ့ရမည်ဖြစ်ပါသည်။

ပုံမှန်ဖြန့်ဝေမှု၏သိပ်သည်းဆလုပ်ဆောင်မှု၏ဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်-

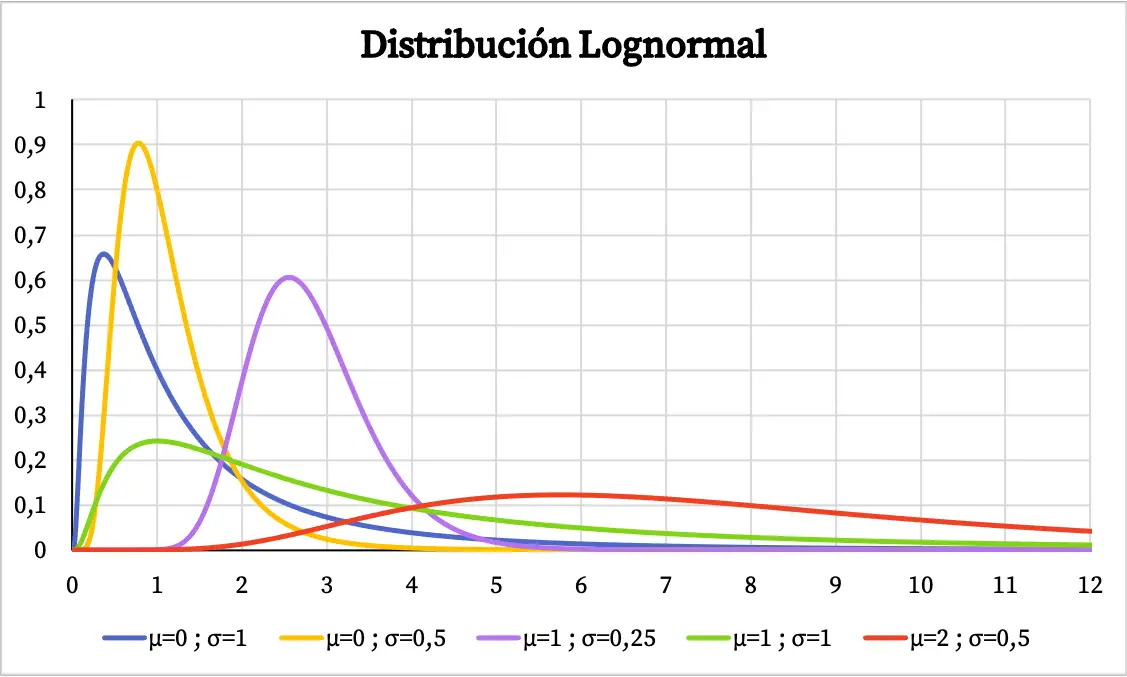
အခြားတစ်ဖက်တွင်၊ ပုံမှန်ဖြန့်ဝေမှု၏ စုစည်းဖြစ်နိုင်ခြေဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်-

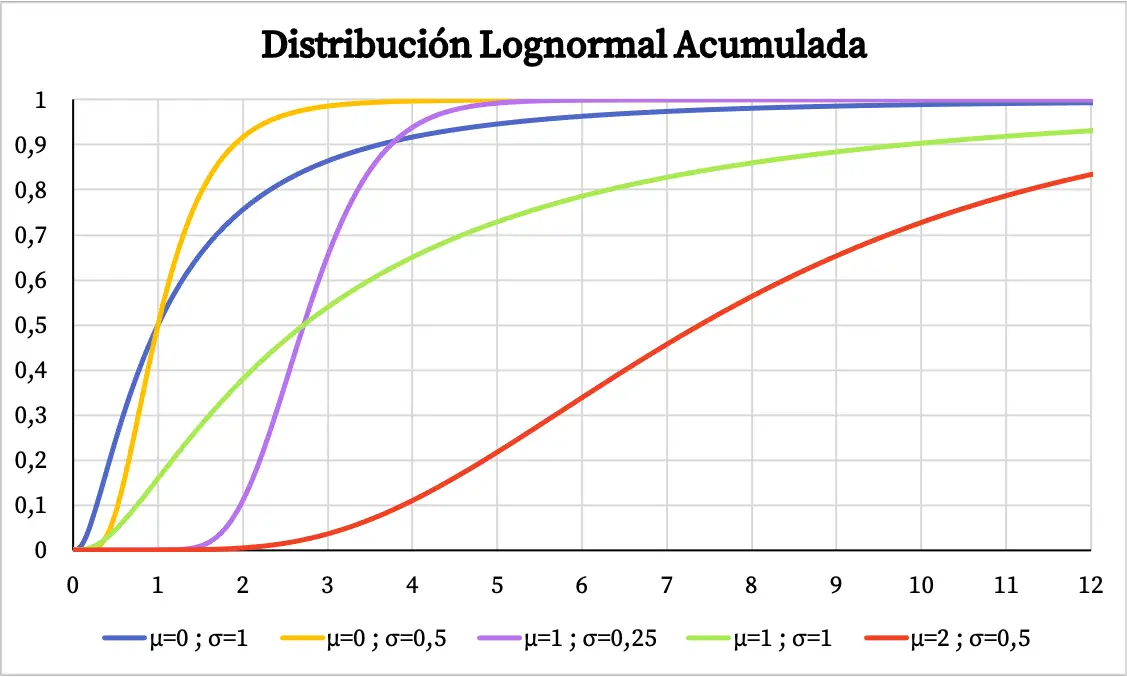
ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေကွက်

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးခြင်း၏ လက္ခဏာများ

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှုတွင် အောက်ပါလက္ခဏာများရှိသည်။

ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုကို ဘောင်နှစ်ခု၏တန်ဖိုး၊ ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှ µ နှင့် ၎င်း၏ကွဲလွဲမှု σ ^{2 တို့} ဖြင့် သတ်မှတ်သည်။

$X\sim \text{Lognormal}(\mu,\sigma^2)$

လော့ဂရစ်သမ်သည် အနုတ် သို့မဟုတ် သုညတန်ဖိုးများကို လက်မခံသောကြောင့် လော့ဂရစ်သမ်သည် အနုတ်လက္ခဏာ သို့မဟုတ် သုညတန်ဖိုးများကို လက်မခံနိုင်သောကြောင့် ပုံမှန်ဖြန့်ဝေမှု၏ ဒိုမိန်းတွင် အပြုသဘောရှိသော ကိန်းဂဏာန်းများပါရှိသည်။

$x\in (0,+\infty)$

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှုတစ်ခု၏မျှော်လင့်ချက်သည် ပျမ်းမျှ၏ပေါင်းလဒ်နှင့် နှစ်ခုဖြင့်ခွဲထားသောကွဲလွဲမှုအား e နှင့်ညီမျှသည်။

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

အခြားတစ်ဖက်တွင်၊ ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်နိုင်သည်-

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှု၏မုဒ်သည် ဖြန့်ဖြူးမှု၏ပျမ်းမျှသို့ မြှင့်တင်ထားသော နံပါတ် e နှင့် ညီမျှသည်။

$Mo=e^\mu$

အောက်ဖော်ပြပါ ပုံသေနည်းကို အသုံးပြုခြင်းဖြင့် ပုံမှန်ဖြန့်ဝေမှု၏ လွဲချော်နေသော ကိန်းဂဏန်းကို ဆုံးဖြတ်နိုင်သည်-

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

ပုံမှန်ဖြန့်ဝေမှု၏ သိပ်သည်းဆလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

ပုံမှန်ဖြန့်ဝေမှု၏ စုစည်းဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

ရွှေ

$\Phi$

စံပုံမှန်ဖြန့်ဝေမှု ၏ စုစည်းဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်ဖြစ်သည်။

ပုံမှန်ဖြန့်ဝေမှုတစ်ခု၏ ဂဏန်းသင်္ချာပျမ်းမျှသည် ၎င်း၏ပျမ်းမျှတန်ဖိုးထက် ကြီးသည်။

$\mu > Me” title=” Rendered by QuickLaTeX.com” height=” 16″ width=” 61″ style=” vertical-align: -4px;” ></p></p> </div>  <div class=$

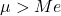
စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှု ဇာတ်ကွက်

ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးခြင်း၏ လက္ခဏာများ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။