ကွဲလွဲမှု
ဤဆောင်းပါးတွင် ကိန်းဂဏန်းများ ကွဲလွဲမှုမှာ အဘယ်အရာဖြစ်ကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ quasivariance ကို တွက်ချက်နည်း၊ ဖြေရှင်းထားသော လေ့ကျင့်ခန်း နှင့် quasivariance နှင့် varianance အကြား ကွာခြားချက်များ သည် အဘယ်နည်း။ ထို့အပြင်၊ သင်သည်အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့်မည်သည့်ဒေတာအစုံ၏ကွဲပြားမှုကိုတွက်ချက်နိုင်သည်။
ကွဲလွဲမှုဆိုတာ ဘာလဲ?
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ quasivariance သည် နမူနာတစ်ခု၏ ကွဲပြားမှုကို ညွှန်ပြသော ပြန့်ကျဲနေသော အတိုင်းအတာတစ်ခုဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ quasivariance သည် ရှုမြင်မှုစုစုပေါင်း အနှုတ်တစ်ခုဖြင့် ပိုင်းခြားထားသော သွေဖည်မှုများ၏ နှစ်ထပ်ကိန်းများနှင့် ညီမျှသည်။
ခြားနားခြင်းအတွက် သင်္ကေတသည် ဖြစ်၏။
![]()
ဖြစ်ဖြစ်၊
![]()
. တခါတရံမှာ သင်္ကေတကိုလည်း သုံးတယ်။
![]()
quasivariance ကိုကိုယ်စားပြုရန်။
Quasivariance ကို ဘက်မလိုက်ဘဲ ကွဲလွဲမှုကို ရှောင်ရှားနေစဉ်နမူနာတစ်ခု၏ ကွဲလွဲမှုကို ဆုံးဖြတ်ရန် အသုံးပြုသည်၊ ထို့ကြောင့် ၎င်းကို ဘက်မလိုက်သောကွဲလွဲမှုဟု မကြာခဏခေါ်သည်။ ထို့ကြောင့် quasivariance သည် လူဦးရေကွဲပြားမှု၏ ကောင်းသော ခန့်မှန်းချက်ဖြစ်သည်။ အမှန်မှာ၊ နမူနာကွဲလွဲမှုကို တွက်ချက်သောအခါ၊ ကွဲလွဲမှုပုံစံဖော်မြူလာကို ကွဲလွဲမှုဖော်မြူလာအစား မကြာခဏအသုံးပြုသည်။ အောက်တွင် ဤစာရင်းအင်းဆိုင်ရာ တိုင်းတာမှုနှစ်ခုကြား ခြားနားချက်အကြောင်း အသေးစိတ်ကို အောက်တွင် ဖော်ပြပါမည်။
Quasivariance ဖော်မြူလာ
quasivariance ကို တွက်ချက်ရန်၊ တန်ဖိုးများနှင့် data set ၏ mean အကြား ခြားနားချက်၏ နှစ်ထပ်ကိန်းများကို ရှာရန်လိုအပ်ပြီး နောက်ပိုင်းတွင် ၎င်းကို စုစုပေါင်း data အရေအတွက် အနှုတ် 1 ဖြင့် ပိုင်းခြားပါ။
ထို့ကြောင့် quasivariance ကို တွက်ချက်ရန် ဖော်မြူလာ မှာ အောက်ပါအတိုင်း ဖြစ်သည်။

ရွှေ-
-
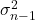
ကွဲလွဲမှု ဖြစ်၏။
-

ဒေတာတန်ဖိုး

.
-

ဒေတာစုစုပေါင်းအရေအတွက်ဖြစ်သည်။
-

data set ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
👉 မည်သည့်ဒေတာအစုံ၏ ကွဲပြားမှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။
n-1 နဲ့ n ကိုမခွဲဘဲ ဘာကြောင့် ခွဲတာလဲ သိချင်နေပါလိမ့်မယ်။ ကောင်းပြီ၊ ဘက်လိုက်မှုကို ဖယ်ရှားခြင်းအကြောင်းဖြစ်သည်၊ ဤနည်းဖြင့် ကျွန်ုပ်တို့သည် ဘက်မလိုက်သော ခန့်မှန်းချက်တစ်ခုကို ရရှိနိုင်သည်။ ထို့ကြောင့် quasivariance သည် လူဦးရေကွဲလွဲမှု၏ ကောင်းမွန်သော ခန့်မှန်းချက်တစ်ခု အဘယ်ကြောင့်ဖြစ်သည်။
quasivariance တွက်ချက်မှု ဥပမာ
ယခု ကျွန်ုပ်တို့သည် quasivariance ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို သိရှိပြီး၊ ကျွန်ုပ်တို့သည် ရိုးရှင်းသော ဥပမာတစ်ခုကို ဖြေရှင်းပါမည်၊ သို့မှသာ ဒေတာစီးရီးတစ်ခု၏ quasivariance ကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်မြင်နိုင်မည်ဖြစ်သည်။
- နိုင်ငံစုံကုမ္ပဏီတစ်ခုမှ ကျွန်ုပ်တို့သည် ပြီးခဲ့သည့်ငါးနှစ်အတွင်း ရရှိခဲ့သော စီးပွားရေးရလဒ်ကို သိရှိကြပြီး အများစုမှာ အမြတ်အစွန်းများရရှိခဲ့သော်လည်း တစ်နှစ်လျှင် ယူရို ၁၁.၅၊ ၂၊ -၉၊ ၇ သန်းအထိ အများအပြား ဆုံးရှုံးခဲ့သည်။ ဤဒေတာအတွဲ၏ ကွဲပြားမှုကို တွက်ချက်ပါ။
ဒေတာအတွဲတစ်ခု၏ quasivariance ကိုရရှိရန် ပထမဆုံးလုပ်ဆောင်ရမည့်အရာမှာ ၎င်း၏ဂဏန်းသင်္ချာဆိုလိုအား တွက်ချက်ရန်ဖြစ်သည်-
![]()
ဒေတာ၏ ပျမ်းမျှတန်ဖိုးကို သိသည်နှင့်၊ quasivariance ဖော်မြူလာကို အသုံးပြုသည်-
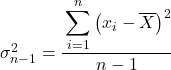
ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် လေ့ကျင့်ခန်း ညွှန်ကြားချက်မှ ပေးထားသော အချက်အလက်ကို ဖော်မြူလာအဖြစ် အစားထိုးသည်-
![]()
နောက်ဆုံးတွင်၊ quasivariance ကိုတွက်ချက်ရန် လုပ်ဆောင်ချက်များကို ဖြေရှင်းရန် လုံလောက်ပါသည်။
![Rendered by QuickLaTeX.com \begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d64d58e69b766d9075ec1220386d8c0_l3.png)
quasivariance ၏ ယူနစ်များသည် ကိန်းဂဏန်းအချက်အလက်များ၏ ယူနစ်များနှင့် တူညီသော်လည်း နှစ်ထပ်ကိန်းဖြစ်သောကြောင့် ဤဒေတာအတွဲ၏ quasivariance သည် 57.2 သန်း 2 ဖြစ်သည်။
Quasivariance ဂဏန်းတွက်စက်
၎င်း၏ ကွဲပြားမှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်း အချက်အလက် သတ်မှတ်မှု ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။
ကွဲလွဲမှုနှင့် ကွဲလွဲမှု
နောက်ဆုံးတွင်၊ ကွဲကွဲပြားပြားနှင့် ကွဲလွဲမှုအကြား ခြားနားချက်ကို ကျွန်ုပ်တို့တွေ့မြင်ရမည်၊ အကြောင်းမှာ ၎င်းတို့၏ အမည်တွင် တူညီနေသော်လည်း ၎င်းတို့ကိုလည်း အလွန်တူညီစွာ တွက်ချက်ထားသောကြောင့် ဖြစ်သည်။
ကွဲကွဲပြားပြားနှင့် ကွဲလွဲမှုအကြား ခြားနားချက် မှာ ဖော်မြူလာ၏ ပိုင်းခြေဖြစ်သည်။ quasivariance ကို တွက်ချက်ရန် n-1 ဖြင့် ပိုင်းရမည်၊ သို့သော် ကွဲလွဲမှုကို n ဖြင့် တွက်ခြင်းဖြင့် တွက်ချက်ပါသည်။
ထို့ကြောင့်၊ quasivariance နှင့် variance သည် သင်္ချာအရ ဆက်စပ်နေသည်၊ quasivariance သည် n (ဒေတာစုစုပေါင်းအရေအတွက်) နှင့် n-1 ဖြင့် ပိုင်းထားသော varianance နှင့် ညီမျှသောကြောင့် ဖြစ်သည်။
![]()
ထို့ကြောင့် တူညီသောဒေတာအတွဲအတွက်၊ quasivariance တန်ဖိုးသည် ကွဲလွဲမှုတန်ဖိုးထက် အမြဲကြီးနေမည်ဖြစ်သည်။