R တွင် bray-curtis ကွဲပြားမှုကို တွက်နည်း

Bray-Curtis ကွဲပြားမှု သည် မတူညီသောဆိုဒ်နှစ်ခုကြားရှိ ကွဲပြားမှုကိုတိုင်းတာသည့်နည်းလမ်းတစ်ခုဖြစ်သည်။

၎င်းကို ဂေဟဗေဒနှင့် ဇီဝဗေဒတွင် ဆိုက်နှစ်ခုကြားရှိ ကွာခြားချက်ကို တွက်ချက်ရန် ထိုနေရာများတွင် တွေ့ရသော မျိုးစိတ်များအကြောင်း မကြာခဏ အသုံးပြုသည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

ရွှေ-

• C _ij : ဆိုက်တစ်ခုစီတွင်တွေ့ရှိရသော မျိုးစိတ်များအတွက် အနိမ့်ဆုံးတန်ဖိုးများ ပေါင်းလဒ်။
• S _i : site i တွင် ရေတွက်ထားသော နမူနာစုစုပေါင်း အရေအတွက်
• S _j : site j တွင်ရေတွက်ထားသောနမူနာစုစုပေါင်းအရေအတွက်

Bray-Curtis တူညီမှုမှာ 0 နှင့် 1 ကြားတွင် အမြဲရှိနေသည်-

• ၀က် ဆိုက်နှစ်ခုသည် တူညီမှုမရှိဟု ဖော်ပြသည်။ တစ်နည်းဆိုရသော် ၎င်းတို့သည် မျိုးစိတ်တစ်ခုစီ၏ တူညီသောအရေအတွက်ကို မျှဝေပါသည်။
• 1 သည် ဝဘ်ဆိုက်နှစ်ခုတွင် လုံးဝတူညီမှုရှိကြောင်း ညွှန်ပြသည်။ တစ်နည်းဆိုရသော် ၎င်းတို့သည် အမျိုးအစားတူမျိုးစိတ်များကို မျှဝေခြင်းမပြုပါ။

ဥပမာအားဖြင့်၊ ရုက္ခဗေဒပညာရှင်တစ်ယောက်သည် ကွဲပြားသောနေရာနှစ်ခုတွင် မတူညီသော အပင်မျိုးစိတ်ငါးမျိုး (A, B, C, D, E) ကို ရေတွက်သည်ဆိုပါစို့။

အောက်ပါဇယားသည် သူစုဆောင်းထားသော အချက်အလက်ကို အကျဉ်းချုပ်ဖော်ပြသည်-

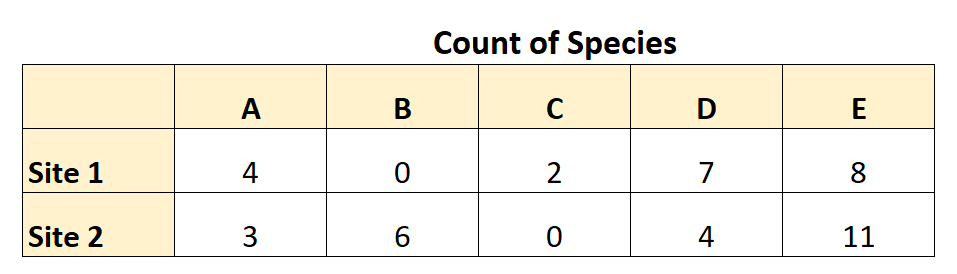
ဤဒေတာကို အသုံးပြု၍ Bray-Curtis ကွဲပြားမှုကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်။

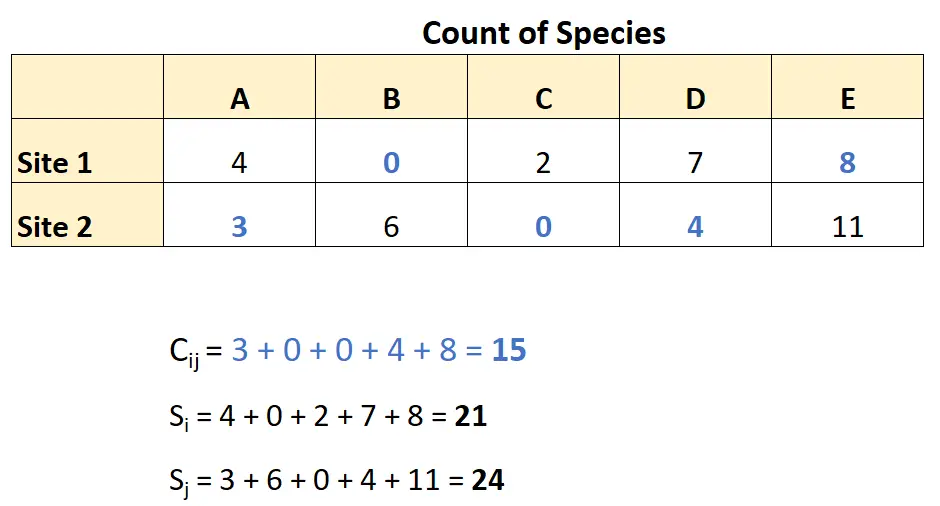
ဤနံပါတ်များကို Bray-Curtis ကွဲပြားခြင်းဖော်မြူလာတွင် ပေါင်းစပ်ခြင်းဖြင့်၊ ကျွန်ုပ်တို့ ရရှိသည်-

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0.33

ဤဆိုဒ်နှစ်ခုကြားရှိ Bray-Curtis ကွဲပြားမှုသည် 0.33 ဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် R တွင် Bray-Curtis ကွဲပြားမှုကို တွက်ချက်ပုံပြသည်။

ဥပမာ- R တွင် Bray-Curtis ကွဲပြားမှုကို တွက်ချက်ခြင်း။

ဦးစွာ၊ ကျွန်ုပ်တို့၏ဒေတာတန်ဖိုးများကိုထိန်းထားရန် အောက်ပါဒေတာဘောင်ကို R တွင်ဖန်တီးကြပါစို့။

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

ဒေတာဘောင်ရှိ အတန်းနှစ်ခုကြားရှိ Bray-Curtis ကွဲပြားမှုကို တွက်ချက်ရန် အောက်ပါကုဒ်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Bray-Curtis သည် 0.33 ကွဲပြားသည်။

၎င်းသည် အစောပိုင်းက ကျွန်ုပ်တို့ကိုယ်တိုင်တွက်ချက်ထားသော တန်ဖိုးနှင့် ကိုက်ညီပါသည်။

မှတ်ချက် – ဒေတာဘောင်ရှိ အတန်းတစ်ခုစီသည် သီးခြားဆိုက်တစ်ခုကို ကိုယ်စားပြုမှသာ ဤဖော်မြူလာသည် အလုပ်လုပ်မည်ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားဆင်တူသည့် မက်ထရစ်များကို တွက်ချက်နည်းကို ရှင်းပြသည်-

R တွင် Jaccard တူညီမှုကို တွက်နည်း
R တွင် cosine တူညီမှုကို တွက်နည်း