အချိုးအစားနမူနာ ဖြန့်ဝေခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် စာရင်းအင်းဆိုင်ရာ အချိုးအစားနမူနာခွဲဝေမှုကား အဘယ်နည်းကို ရှင်းပြထားသည်။ အလားတူပင်၊ အချိုးအစားနမူနာဖြန့်ချီရေးဖော်မြူလာကို တွေ့ရမည်ဖြစ်ပြီး၊ ထို့အပြင်၊ အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကိုလည်း တွေ့ရပါမည်။

အချိုးအစားနမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။

အချိုးအစားနမူနာဖြန့်ဝေခြင်း (သို့မဟုတ် အချိုးအစားနမူနာဖြန့်ဝေခြင်း ) သည် လူဦးရေတစ်ခုစီမှ ဖြစ်နိုင်သည့်နမူနာတစ်ခုစီ၏ အချိုးအစားကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဖြူးမှုဖြစ်သည်။ ဆိုလိုသည်မှာ လူဦးရေမှ ဖြစ်နိုင်ခြေရှိသောနမူနာများအားလုံး၏ နမူနာအချိုးများသည် အချိုးအစားနမူနာခွဲဝေမှုကို ဖြစ်စေသည်။

တစ်နည်းအားဖြင့်ဆိုရသော် လူဦးရေတစ်ခုစီ၏နမူနာတစ်ခုစီ၏နမူနာအချိုးအစားကိုရွေးချယ်နိုင်သောနမူနာအားလုံးကိုလေ့လာခြင်းဖြင့်ရရှိသောအချိုးအစားနမူနာကိုရရှိခြင်းဖြစ်သည်။ ထို့ကြောင့် တွက်ချက်ထားသောနမူနာအချိုးအစားအစုသည် အချိုးအစားနမူနာခွဲဝေမှုကို ဖွဲ့စည်းသည်။

နမူနာခွဲဝေမှု၏အချိုးအစားသည် ဘာအတွက်ဖြစ်သည်ကို သင်အံ့သြနေပါက၊ နမူနာတစ်ခုတည်းကို ခွဲခြမ်းစိတ်ဖြာသောအခါ လူဦးရေအချိုးအစားတန်ဖိုးသို့ချဉ်းကပ်နိုင်ခြေကို တွက်ချက်ရန်အတွက် စာရင်းဇယားများတွင် ၎င်းကိုအသုံးပြုသည်။

➤ ဆိုလိုတာက နမူနာဖြန့်ချီတာကို ကြည့်ပါ။

အချိုးကျနမူနာဖြန့်ဝေမှုဖော်မြူလာ

တကယ်တော့၊ နမူနာတစ်ခုရဲ့ အချိုးအစားတစ်ခုကို လေ့လာတဲ့အခါ၊ အောင်မြင်မှုကိစ္စတွေကို ခွဲခြမ်းစိတ်ဖြာပါတယ်။ ထို့ကြောင့်၊ လေ့လာမှုရှိ ကျပန်းကိန်းရှင်သည် binomial probability ဖြန့်ဝေမှု နောက်ဆက်တွဲဖြစ်သည်။

ဗဟိုကန့်သတ်သီအိုရီအရ၊ ကြီးမားသောအရွယ်အစားများ (n>30) အတွက် ကျွန်ုပ်တို့သည် သာမန်ဖြန့်ဖြူးမှုတစ်ခုနှင့် ပို၍နီးကပ်စွာ binomial distribution ကို ယူဆောင်လာနိုင်သည်။ ထို့ကြောင့်၊ အချိုးအစားနမူနာဖြန့်ဝေမှုသည် အောက်ပါဘောင်များနှင့်အတူ ပုံမှန်ဖြန့်ဖြူးမှုကို ခန့်မှန်းသည်-

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

ရွှေ

$p$

အောင်မြင်မှု၏ ဖြစ်နိုင်ခြေနှင့်

$q$

ပျက်ကွက်ခြင်း၏ ဖြစ်နိုင်ခြေဖြစ်သည်။

$q=1-p$

မှတ်ချက်- အကယ်၍ binomial ဖြန့်ဝေမှုသည် သာမန်ဖြန့်ဝေမှုတစ်ခုနှင့်သာ ခန့်မှန်းနိုင်သည်။

$n>30″ title=” Rendered by QuickLaTeX.com” height=” 14″ width=” 52″ style=” vertical-align: -2px;” > ၊ <p class=$ $np\ge 5$

နှင့်

$nq\ge 5$

➤ ပုံမှန် ဖြန့်ဝေမှု နမူနာများကို ကြည့်ပါ။

ထို့ကြောင့်၊ အချိုးအစားနမူနာခွဲဝေမှုကို ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုအဖြစ် ခန့်မှန်းနိုင်သောကြောင့်၊ နမူနာတစ်ခု၏ အချိုးအစားနှင့်ဆက်စပ်သည့် ဖြစ်နိုင်ခြေမှန်သမျှကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

ရွှေ-

$\widehat{p}$

နမူနာအချိုးဖြစ်သည်။
$p$

လူဦးရေအချိုးအစားဖြစ်ပါသည်။
$q$

လူဦးရေ၏ ကျရှုံးမှုဖြစ်နိုင်ခြေ၊

$q=1-p$

.
$n$

နမူနာအရွယ်အစားဖြစ်သည်။
$Z$

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။

အချိုးအစားနမူနာဖြန့်ဝေခြင်း၏ ကွန်ကရစ်နမူနာ

Proportion Sampling Distribution ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဆက်စပ်ဖော်မြူလာများဟူသည် သဘောတရားကို အပြည့်အဝနားလည်ရန် အောက်တွင် တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းထားသော ဥပမာတစ်ခုကို ပေးထားပါသည်။

စက်မှုကုမ္ပဏီတစ်ခုသည် အစိတ်အပိုင်းများကို ၃ ရာခိုင်နှုန်းသာ ချို့ယွင်းနေသော အစိတ်အပိုင်းများ ထုတ်လုပ်ရန် အခိုင်အမာဆိုထားသော စက်ရုံမှ အစိတ်အပိုင်းများကို ဝယ်ယူသည်။ ဒါကိုစစ်ဆေးဖို့အတွက် ကုမ္ပဏီက အစိတ်အပိုင်း 500 ရဲ့ အမှာစာတစ်ခုကို ခွဲခြမ်းစိတ်ဖြာဖို့ ဆုံးဖြတ်လိုက်ပါတယ်။ နမူနာတွင် ချို့ယွင်းချက် 5% ထက်ပိုသော အစိတ်အပိုင်းများကို ရှာဖွေရန် ဖြစ်နိုင်ခြေရှိသနည်း။

ဤအခြေအနေတွင်၊ ကျွန်ုပ်တို့လေ့လာလိုသော လူဦးရေအချိုးအစားသည် 0.03 ဖြစ်သောကြောင့် ကန့်သတ်ချက် q သည် 0.97 နှင့် ညီမျှသည်။

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

ထို့ကြောင့်၊ ၎င်းတို့မေးသော ဖြစ်နိုင်ခြေကို ရှာရန်၊ ကျွန်ုပ်တို့သည် ယခင်အပိုင်းတွင် တွေ့ခဲ့သည့် ဖော်မြူလာကို အသုံးပြုခြင်းဖြင့် သက်ဆိုင်ရာ စာရင်းအင်းကို တွက်ချက်ရပါမည်-

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

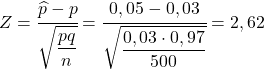
ထို့ကြောင့် ချို့ယွင်းနေသော အစိတ်အပိုင်းများ 5% ကျော်ရရှိရန် ဖြစ်နိုင်ခြေသည် အောက်ပါဖြစ်နိုင်ခြေနှင့် ညီမျှသည်-

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 360″ style=” vertical-align: -5px;” > နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် <a href=$ Z ဖြန့်ဖြူးမှုဇယား တွင် P[Z≤2.62] ဖြစ်နိုင်ခြေကို ရှာဖွေပြီး ပြဿနာမေးသည့် ဖြစ်နိုင်ခြေကို တွက်ချက်သည်-

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=” Rendered by QuickLaTeX.com” height=” 167″ width=” 162″ style=” vertical-align: 0px;” > နိဂုံးချုပ်အားဖြင့်၊ ခွဲခြမ်းစိတ်ဖြာထားသောနမူနာတွင် ချို့ယွင်းချက် 5% ထက်ပိုသော အစိတ်အပိုင်းများကို ရှာဖွေရန် ဖြစ်နိုင်ခြေမှာ 0.44% ဖြစ်သည်။ </div>  <div class=$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

အချိုးအစားနမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။

အချိုးကျနမူနာဖြန့်ဝေမှုဖော်မြူလာ

အချိုးအစားနမူနာဖြန့်ဝေခြင်း၏ ကွန်ကရစ်နမူနာ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။