ဆုံးဖြတ်ခြင်းဆိုင်ရာ ကိန်းဂဏန်း (r နှစ်ထပ်ကိန်း)

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် ပြဌာန်းခြင်း၏ကိန်းဂဏန်း (သို့မဟုတ် R စတုရန်း) ဟူသည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ဆုံးဖြတ်ခြင်း၏ coefficient တွက်ချက်နည်း၊ ၎င်းကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံနှင့် ဒေတာနမူနာတစ်ခု၏ ကိန်းဂဏန်းသတ်မှတ်ခြင်းဆိုင်ရာ ကိန်းဂဏန်းများကို တွက်ချက်ရန် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်ပါသည်။

ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်း (R နှစ်ထပ်ကိန်း) ကဘာလဲ။

R ² ( R နှစ်ထပ်ကိန်း ) သင်္ကေတဖြစ်သော ဆုံးဖြတ်ချက်ချခြင်း၏ကိန်းဂဏန်း သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အံဝင်ခွင်ကျကောင်းမွန်မှုကို တိုင်းတာသည့် ကိန်းဂဏန်းတစ်ခုဖြစ်သည်။ ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်းသည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုသည် ဒေတာအစုတစ်ခုနှင့် မည်မျှကိုက်ညီကြောင်းပြသသည်၊ ဆိုလိုသည်မှာ၊ ဆုတ်ယုတ်မှုပုံစံဖြင့် ရှင်းပြထားသော ရာခိုင်နှုန်းကို ညွှန်ပြသည်။

ထို့ကြောင့်၊ ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်း မြင့်မားလေ၊ ဆုတ်ယုတ်မှုပုံစံသည် ပိုကောင်းလေဖြစ်သည်။ ဤအခြေအနေသည် အမြဲတမ်းမပြည့်မီသော်လည်း၊ ကျွန်ုပ်တို့သည် မူအရအားဖြင့် ဖြစ်နိုင်သမျှကြီးမားသော ဆုံးဖြတ်ခြင်းဆိုင်ရာကိန်းဂဏန်းကို စိတ်ဝင်စားပါသည်။ အဆုံးအဖြတ်၏ coefficient ကို မည်သို့အနက်ပြန်ဆိုရမည်ကို အောက်တွင်ဖော်ပြထားသည်။

Coefficient ကို ဆုံးဖြတ်ခြင်း ဖော်မြူလာ

အဆုံးအဖြတ်ပေးသောကိန်းသည် ကျန်ရှိသောကွဲလွဲချက်နှင့် မှီခိုကိန်းရှင်၏ကွဲလွဲမှုအကြား အချိုးအနုတ်တစ်ခုနှင့် ညီမျှသည်။ အဆုံးအဖြတ်၏ ကိန်းဂဏန်းအား လေးထောင့်စုစုပေါင်း၏ ပေါင်းလဒ်များအတွင်း အကြွင်းအကျန်များမှ တစ်နှုတ်နှုတ်ကိန်းများကို နုတ်ခြင်းဖြင့်လည်း တွက်ချက်နိုင်သည်။

ထို့ကြောင့် coefficient of determination ကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်း ဖြစ်ပါသည်။

ကိန်းဂဏန်းသတ်မှတ်ခြင်းအတွက် ဖော်မြူလာ၊ r စတုရန်းအတွက် ဖော်မြူလာ

ရွှေ-

$R^2$

အဆုံးအဖြတ်၏ကိန်းဂဏန်းဖြစ်သည်။
$\sigma_r^2$

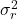
ကျန်ရှိသောကွဲလွဲမှုဖြစ်သည်။
$\sigma^2$

မှီခိုပြောင်းလဲနိုင်သော Y ၏ကွဲလွဲမှုဖြစ်သည်။
$y_{i}$

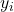
observation dependent variable i ၏တန်ဖိုးဖြစ်သည်။
$\widehat{y}_{i}$

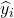
ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးသည် i.
$\overline{y}$

လေ့လာသုံးသပ်မှုအားလုံးရှိ မှီခိုကိန်းရှင်၏ ဆိုလိုရင်းဖြစ်သည်။

👉 မည်သည့်ဒေတာအစုံအတွက်မဆို coefficient of determination ကိုတွက်ချက်ရန် အောက်ပါ calculator ကိုသုံးနိုင်သည်။

linear regression model ၏ဖြစ်ရပ်အတွက်၊ ဆုံးဖြတ်ခြင်း၏ coefficient သည် correlation coefficient ၏စတုရန်းနှင့် ညီမျှသည်-

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

ရွှေ

$\sigma_{XY}^2$

ကိန်းရှင် X နှင့် Y တို့၏ ကွဲလွဲမှု ၊

$\sigma_X^2$

နှင့်

$\sigma_Y^2$

အမှီအခိုကင်းသော ကိန်းရှင် X နှင့် မှီခိုသော ကိန်းရှင် Y တို့၏ ကွဲလွဲမှုများ အသီးသီးဖြစ်သည်။

Coefficient of Determination Calculator

ရိုးရှင်းသော linear regression model နှင့် ကိုက်ညီပြီး ၎င်း၏ coefficient of determination ကို တွက်ချက်ရန် အောက်တွင် နမူနာဒေတာကို ဂဏန်းပေါင်းစက်ထဲသို့ ထည့်ပါ။ သင်သည် ဒေတာအတွဲများကို ခွဲခြားထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ပထမအကွက်တွင် အမှီအခိုကင်းသော ကိန်းရှင် X ၏ တန်ဖိုးများသာ ရှိပြီး ဒုတိယအကွက်တွင် မှီခိုနေသော ကိန်းရှင် Y ၏ တန်ဖိုးများသာ ရှိနေမည်ဖြစ်သည်။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အဆုံးအဖြတ်၏ ကိန်းဂဏန်းကို အဓိပ္ပာယ်ပြန်ဆိုခြင်း။

ဤအပိုင်းတွင် သင်က ဘာကိုဆိုလိုသည်ကို သင်မသိပါက နောက်ပိုင်းတွင် ဆုံးဖြတ်ခြင်း၏ coefficient ၏တန်ဖိုးကို သိရှိရန်အချက်မရှိသောကြောင့် ဤအပိုင်းတွင် ဆုံးဖြတ်ခြင်း၏ ဖော်ကိန်းကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

ဆုံးဖြတ်ခြင်း၏ ကိန်းဂဏန်းတန်ဖိုးသည် 0 မှ 1 အထိ ရှိနိုင်သော်လည်း၊ ၎င်းကို များသောအားဖြင့် ရာခိုင်နှုန်းအဖြစ် ဖော်ပြသည်၊ ထို့ကြောင့် အနိမ့်ဆုံးမှာ 0% ဖြစ်ပြီး အမြင့်ဆုံးမှာ 100% ဖြစ်သည်။

ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်း၏အဓိပ္ပာယ်ဖွင့်ဆိုချက် နှင့်ပတ်သက်၍ ၎င်း၏တန်ဖိုးသည် မြင့်မားလေလေ ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာနမူနာကို ပိုမိုကောင်းမွန်စွာရှင်းပြသည်ကို ဆိုလိုသည်။ ထို့ကြောင့်၊ ဆုံးဖြတ်ခြင်း၏ coefficient သည် 1 သို့ ပိုနီးစပ်လေ၊ မော်ဒယ်ကို ချိန်ညှိလေလေ ဖြစ်သည်။ အခြားတစ်ဖက်တွင်၊ ၎င်းသည် 0 နှင့် နီးကပ်လေ၊ ထုတ်လုပ်ထားသော regression model သည် ယုံကြည်စိတ်ချရမှုနည်းလေဖြစ်သည်။

သို့ရာတွင်၊ ဆုတ်ယုတ်မှုပုံစံနှစ်ခုကို နှိုင်းယှဉ်သောအခါ၊ ပိုမိုမြင့်မားသော ဆုတ်ယုတ်မှုကိန်းဂဏန်းဖြင့် မော်ဒယ်သည် အမြဲတမ်းပိုကောင်းမည်မဟုတ်ပေ။ ဥပမာအားဖြင့်၊ regression model တစ်ခုတွင် regression coefficient R ² = 100% ရှိနိုင်သည်၊ အကြောင်းမှာ၊ အကြောင်းမှာ ရှင်းလင်းချက်များစွာသော variable များကို မော်ဒယ်တွင် ထည့်သွင်းထားပြီးဖြစ်သောကြောင့်၊ လေ့လာတွေ့ရှိချက်အားလုံးကို ပြီးပြည့်စုံစွာ ရှင်းပြနိုင်ပါသည်။ သို့သော် ဤပုံစံသည် ဆုတ်ယုတ်မှုပုံစံကိုတည်ဆောက်ရန် အသုံးမပြုခဲ့သော တန်ဖိုးအသစ်အတွက် အလွန်ညံ့ဖျင်းသော ခန့်မှန်းချက်တစ်ခုကို သေချာပေါက်ပြုလုပ်သည်။

ရလဒ် ဆုတ်ယုတ်မှုပုံစံသည် ယခင်ယူဆချက်များနှင့် ကိုက်ညီကြောင်းလည်း မှတ်သားထားသင့်သည်။ ထို့ကြောင့်၊ အကြွင်းအကျန်များ၏ ကွဲပြားမှုမှာ မတည်မြဲခြင်း (homoscedasticity) မရှိလျှင် အလွန်မြင့်မားသော ကိန်းသေသတ်မှတ်မှုရှိသော မော်ဒယ်သည် အသုံးမဝင်ပေ။

ထို့အပြင်၊ အဆုံးအဖြတ်ပေးသည့်ကိန်းဂဏန်းသည် ရှင်းလင်းချက်ဆိုင်ရာကိန်းရှင်များပါ၀င်မှုကို အပြစ်ပေးခြင်းမရှိသောကြောင့် အရေးကြီးသောကန့်သတ်ချက်တစ်ခုရှိသည် ။ ယုတ္တိနည်းအရ၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင် ရှင်းပြနိုင်သော ကိန်းရှင်များ ပိုများလေ၊ မော်ဒယ်သည် ပို၍ရှုပ်ထွေးလေဖြစ်သော်လည်း ၎င်းသည် လေ့လာတွေ့ရှိထားသောဒေတာကို ရှင်းပြလေလေ၊ ထို့ကြောင့်၊ အဆုံးအဖြတ်ပေးသောကိန်းဂဏန်းသည် ပိုမိုမြင့်မားလေဖြစ်သည်။ သို့သော်လည်း၊ ချိန်ညှိထားသော ကိန်းဂဏန်းသည် မော်ဒယ်ရှိ ကိန်းရှင်အရေအတွက်ကို ထည့်သွင်းစဉ်းစားသည် (၎င်းကို အောက်တွင် တွက်ချက်ပုံကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်)။

နိဂုံးချုပ်အနေနှင့်၊ ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာအစုံနှင့် မည်မျှကိုက်ညီသည်ကို သိရှိနိုင်သောကြောင့် နိဂုံးချုပ်အားဖြင့် အဆုံးအဖြတ်ပေးသည့်ကိန်းဂဏန်းသည် ဆုတ်ယုတ်မှုပုံစံကို ပိုင်းခြားစိတ်ဖြာရန် အလွန်အသုံးဝင်ပါသည်။ သို့သော်၊ ကိန်းဂဏန်းဂရပ်များ ကဲ့သို့သော ရလဒ်ပုံစံကို ပြန်လည်သုံးသပ်ရန် အခြားကိရိယာများကိုလည်း အသုံးပြုသင့်သည်။

ချိန်ညှိဆုံးဖြတ်ခြင်း ကိန်းဂဏန်း

ချိန်ညှိသော ဆုံးဖြတ်ခြင်းဆိုင်ရာ ညှိယူသောကိန်းဂဏန်းသည် ချိန်ညှိသောကိန်းဂဏန်း ဟုလည်း ခေါ်သည်၊၊ မော်ဒယ်တွင်ပါရှိသော ရှင်းပြကိန်းရှင်အရေအတွက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အံဝင်ခွင်ကျကောင်းမွန်မှုကို တိုင်းတာသည်။

ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်းနှင့် ချိန်ညှိသောကိန်းဂဏန်းများ ကြား ခြားနားချက်မှာ ကိန်းရှင်၏အရည်အသွေးကို ထည့်သွင်းတွက်ချက်ခြင်းမရှိဘဲ ချိန်ညှိမှုအရည်အသွေးကို တိုင်းတာခြင်းဖြစ်ပြီး အခြားတစ်ဖက်တွင်၊ ချိန်ညှိသောကိန်းဂဏန်းသည် ချိန်ညှိမှုအရည်အသွေးကို တိုင်းတာခြင်းဖြစ်သည်။ ပေါင်းထည့်ထားသော ကိန်းရှင်တစ်ခုစီအတွက် အပြစ်ပေးခြင်း။

ချိန်ညှိထားသော ကိန်းဂဏန်းကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

ရွှေ-

$\bar{R}^2$

ချိန်ညှိထားသော ကိန်းဂဏန်းသည် ဆုံးဖြတ်ချက်တစ်ခုဖြစ်သည်။
$R^2$

အဆုံးအဖြတ်၏ကိန်းဂဏန်းဖြစ်သည်။
$N$

နမူနာအရွယ်အစားဖြစ်သည်။
$k$

ဆုတ်ယုတ်မှုပုံစံတွင် ရှင်းပြထားသော ကိန်းရှင်အရေအတွက်များဖြစ်သည်။

ထို့ကြောင့်၊ မော်ဒယ်များတွင် ကွဲပြားသော ရှင်းပြကိန်းရှင်များ အများအပြားရှိနိုင်သောကြောင့်၊ ချိန်ညှိထားသော ကိန်းဂဏန်းသည် မတူညီသော မော်ဒယ်နှစ်ခုကို နှိုင်းယှဉ်ရန် ဆုံးဖြတ်ခြင်းဆိုင်ရာ ကိန်းဂဏန်းထက် ပိုမိုကောင်းမွန်ပါသည်။

➤ ကြည့်ပါ- ချိန်ညှိထားသော ဆုံးဖြတ်ချက်ကိန်းဂဏန်း

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။