လိင်တူဆက်ဆံခြင်း

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် လိင်တူဆက်ဆံခြင်းဟူသည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ homoscedasticity ၏အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ homoscedasticity မရှိခြင်း၏ဆုတ်ယုတ်မှုပုံစံ၏အကြောင်းရင်းများနှင့်အခြားအရာများ၊ ၎င်းကိုမည်သို့ပြုပြင်ရမည်ကိုသင်တွေ့လိမ့်မည်။

လိင်တူဆက်ဆံခြင်းဟူသည် အဘယ်နည်း။

Homoscedasticity သည် အဆက်မပြတ်ကွဲလွဲမှုရှိသည့် ဆုတ်ယုတ်မှုပုံစံ၏ လက္ခဏာတစ်ရပ်ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အမှားအယွင်းကွဲလွဲမှုသည် စဉ်ဆက်မပြတ်ဖြစ်နေသောအခါ၊ အဆိုပါပုံစံသည် မျိုးရိုးဗီဇကိုပြသပြီး ထို့ကြောင့်၊ ၎င်းသည် homoscedastic ပုံစံဖြစ်သည်။

အမှား (သို့မဟုတ် ကျန်ရှိသော) ကို အစစ်အမှန်တန်ဖိုးနှင့် ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးအကြား ကွာခြားချက်အဖြစ် သတ်မှတ်ကြောင်း သတိရပါ။

ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို လုပ်ဆောင်သောအခါ၊ လေ့လာမှုတစ်ခုစီအတွက် ယခင်ဖော်ပြချက်နှင့် မတူညီသောတန်ဖိုးကို ကျွန်ုပ်တို့ရရှိမည်ဖြစ်သည်။ ထို့ကြောင့်၊ homoskedastic statistical model သည် တွက်ချက်ထားသော error များ၏ကွဲလွဲမှုကို လေ့လာသုံးသပ်မှုများတစ်လျှောက်လုံးတွင် အမြဲမပြတ်ရှိနေသော တစ်ခုဖြစ်သည်။

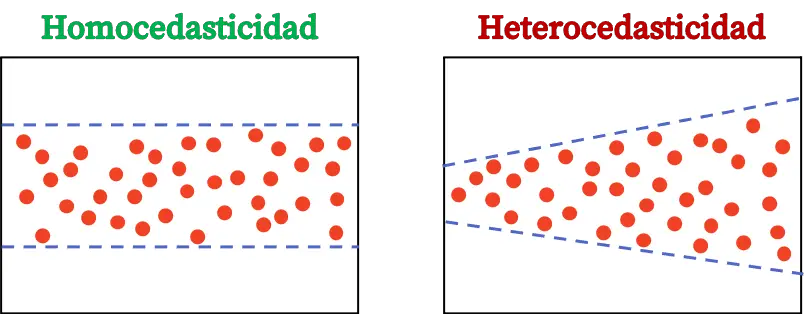
ဆုတ်ယုတ်မှုပုံစံသည် လိင်တူဆက်ဆံမှုကို ပြသရန် အရေးကြီးပါသည်။ တကယ်တော့ ဒါက ဆုတ်ယုတ်မှုပုံစံတွေရဲ့ ယခင်ယူဆချက်တွေထဲက တစ်ခုပါ။ အကြွင်းအကျန်များသည် homoscedastic မဟုတ်ပါက၊ homoscedasticity ရရှိရန် အခြားနည်းလမ်းဖြင့် မော်ဒယ်ကို ပြန်လုပ်ခြင်းက ပိုကောင်းပါတယ်။ မဟုတ်ပါက၊ regression coefficients ၏ ခန့်မှန်းခြေသည် မှားယွင်းဖွယ်ရှိပြီး အယူအဆ စစ်ဆေးမှု တွင် အမှားအယွင်းများ အမှန်တကယ် ပယ်ချသင့်သည့် null hypotheses များကို လက်ခံခြင်းဖြင့် ဖြစ်ပေါ်လာမည်ဖြစ်ပါသည်။

လိင်တူဆက်ဆံခြင်း မရှိခြင်း၏ အကြောင်းရင်းများ

မော်ဒယ်တစ်ခုတွင် လိင်တူဆက်ဆံခြင်း မရှိရသည့် အကြောင်းရင်းများမှာ-

• ဒေတာအကွာအဝေး သည် ပျမ်းမျှထက်စာလျှင် အလွန်ကျယ်ပြန့်သည်။ တူညီသော ကိန်းဂဏန်းနမူနာတွင် အလွန်ကြီးမားသော တန်ဖိုးများနှင့် အလွန်သေးငယ်သော တန်ဖိုးများရှိပါက၊ ရရှိသော ဆုတ်ယုတ်မှုပုံစံသည် တူညီမှုမရှိဟု ဖြစ်နိုင်ခြေရှိသည်။
• ဆုတ်ယုတ်မှုပုံစံရှိ ကိန်းရှင်များကို ချန်လှပ်ထားခြင်းသည် တူညီမှုမရှိခြင်းကိုလည်း ဖြစ်စေသည်။ ယုတ္တိနည်းအားဖြင့်၊ သက်ဆိုင်ရာ ကိန်းရှင်သည် မော်ဒယ်တွင် မပါဝင်ပါက၊ ၎င်း၏ ကွဲလွဲမှုကို ကျန်ရှိသော များတွင် ထည့်သွင်းမည်ဖြစ်ပြီး သေချာပေါက် ပြုပြင်မည်မဟုတ်ပါ။
• ဖွဲ့စည်းတည်ဆောက်ပုံ အပြောင်းအလဲသည် ဒေတာအစုံနှင့် မော်ဒယ်၏ အံဝင်ခွင်ကျ ညံ့ဖျင်းမှုကို ဖြစ်ပေါ်စေနိုင်ပြီး ထို့ကြောင့် ကျန်အကြွင်းအကျန်များ၏ ကွဲလွဲမှုသည် မတည်မြဲပါ။
• အချို့သော ကိန်းရှင်များသည် အခြားရှင်းပြကိန်းရှင်များထက် ပိုကြီးသောတန်ဖိုးများရှိပါက မော်ဒယ်တွင် တူညီမှုမရှိနိုင်ပါ။ ဤကိစ္စတွင်၊ ပြဿနာကိုဖြေရှင်းရန် variable များကို relativized လုပ်နိုင်သည်။

သို့ရာတွင်၊ မျိုးရိုးဗီဇအဖြစ် တင်ပြရန် ခက်ခဲသော အချို့သောကိစ္စများ ရှိပါသည်။ ဥပမာအားဖြင့်၊ လူတစ်ဦး၏ ဝင်ငွေကို ၎င်းတို့၏ စားနပ်ရိက္ခာအသုံးစရိတ်ဖြင့် စံနမူနာပြုပါက၊ ချမ်းသာသောသူများသည် ဆင်းရဲသူများထက် ၎င်းတို့၏ စားနပ်ရိက္ခာအသုံးစရိတ်တွင် များစွာကွာခြားမှုရှိသည်။ အဘယ်ကြောင့်ဆိုသော် ချမ်းသာသူတစ်ဦးသည် စျေးပေါသော စားသောက်ဆိုင်များတွင် အမြဲစားလေ့ရှိသော ဆင်းရဲသူနှင့်မတူဘဲ ဈေးပေါသော စားသောက်ဆိုင်များတွင် တစ်ခါတစ်ရံ စားလေ့ရှိသောကြောင့် ဖြစ်သည်။ ထို့ကြောင့်၊ regression model တွင် homoscedasticity ရရှိရန် ခက်ခဲသည်။

လိင်တူဆက်ဆံခြင်းကို ရရှိရန် ဒေတာကို ပြုပြင်ခြင်း။

ရရှိသော ဆုတ်ယုတ်မှုပုံစံသည် တူညီခြင်းမရှိပါက၊ တူညီသော တူညီမှုရရှိရန် အောက်ပါပြင်ဆင်ချက်များကို ကြိုးပမ်းနိုင်သည်-

• အမှီအခိုကင်းသော ကိန်းရှင်၏ သဘာဝ လော့ဂရစ်သမ်ကို တွက်ချက်ပါ၊ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုသည် ဂရပ်တွင် တိုးလာသောအခါ ယေဘုယျအားဖြင့် အသုံးဝင်သည်။
• ကျန်ရှိသောကွက်ကွက်ပေါ်မူတည်၍ သီးခြားပြောင်းလွဲပြောင်းခြင်း၏ အခြားပုံစံပြောင်းလဲခြင်းသည် ပို၍လက်တွေ့ကျပေမည်။ ဥပမာအားဖြင့်၊ ဂရပ်သည် parabola ပုံသဏ္ဍာန်ဖြစ်နေပါက၊ အမှီအခိုကင်းသော variable ၏စတုရန်းကို တွက်ချက်နိုင်ပြီး ထိုကိန်းရှင်ကို မော်ဒယ်သို့ထည့်နိုင်သည်။
• မော်ဒယ်အတွက် အခြားသော ကိန်းရှင်များကိုလည်း အသုံးပြုနိုင်သည်။ ကိန်းရှင်တစ်ခုကို ဖယ်ရှားခြင်း သို့မဟုတ် ပေါင်းထည့်ခြင်းဖြင့်၊ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုကို ပြင်ဆင်နိုင်သည်။
• အနည်းဆုံး စတုရန်းစံသတ်မှတ်ချက်ကို အသုံးပြုမည့်အစား၊ အလေးချိန်အနည်းဆုံး စတုရန်းစံနှုန်းကို အသုံးပြုနိုင်သည်။

လိင်တူဆက်ဆံခြင်း နှင့် မျိုးကွဲကွဲပြားခြင်း

နောက်ဆုံးတွင်၊ ၎င်းတို့သည် ဆုတ်ယုတ်မှုပုံစံများ၏ အရေးကြီးသော စာရင်းအင်းဆိုင်ရာ အယူအဆနှစ်ခုဖြစ်သောကြောင့် homoskedasticity နှင့် heteroskedasticity အကြား ခြားနားချက်ကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

Heteroscedasticity သည် ဆုတ်ယုတ်မှုပုံစံ၏ ကျန်ရှိသော ကိန်းသေကွဲလွဲမှု မရှိဟု ဆိုလိုသည့် ကိန်းဂဏန်းလက္ခဏာတစ်ခုဖြစ်ပြီး ကွက်ကွက်တစ်လျှောက် အမှားအယွင်းများ၏ ကွဲပြားမှုမှာ မတူညီနိုင်စေရန် ကိန်းသေဖြစ်သည်။

မျိုးတူပွားခြင်း နှင့် မျိုးကွဲကွဲပြားခြင်း အကြား ခြားနားချက် သည် အမှားကွဲလွဲမှု ၏ တည်မြဲမှု ဖြစ်သည်။ Homoskedasticity သည် အမှားကွဲလွဲမှုမှာ စဉ်ဆက်မပြတ်ရှိကြောင်းကို ရည်ညွှန်းပြီး heteroscedasticity သည် အမှားကွဲလွဲမှုကို မတည်မြဲဟု ဆိုလိုသည်။