စာရင်းအင်းဖော်မြူလာများ

အားဖြင့် Benjamin Anderson ဩဂုတ် 1, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤနေရာတွင် ပင်မစာရင်းအင်းဖော်မြူလာများကို တွေ့ရပါမည်။ စာရင်းအင်းဖော်မြူလာတစ်ခုစီ၏ အသုံးချပုံနမူနာများကို သင်တွေ့မြင်နိုင်သည့် ကျွန်ုပ်တို့၏ဆောင်းပါးများနှင့် ချိတ်ဆက်ထားခဲ့ပြီး ထို့အပြင် တွက်ချက်မှုများပြုလုပ်ရန်နှင့် ဖော်မြူလာ၏ရလဒ်ကို တိုက်ရိုက်သိရန်မလိုစေရန် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်အသုံးပြုနိုင်ပါသည်။

ဗဟိုသဘောထား၏ ကိန်းဂဏန်းတိုင်းတာမှုများအတွက် ဖော်မြူလာများ

တစ်ဝက်

ပျမ်းမျှတွက်ချက်ရန်၊ တန်ဖိုးများအားလုံးကို ပေါင်းထည့်ပြီးနောက် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းပါ။ ထို့ကြောင့် ပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

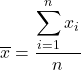
ကိန်းဂဏန်းစာရင်းအင်းများတွင် ပျမ်းမျှ အား ဂဏန်းသင်္ချာ ပျမ်းမျှ သို့မဟုတ် ပျမ်းမျှ ဟုလည်း ခေါ်သည်။

➤ ဂဏန်းသင်္ချာ ပျမ်းမျှဂဏန်းတွက်စက်ကို ကြည့်ပါ။

မီဒီယံ

ပျမ်းမျှ သည် အသေးဆုံးမှ အကြီးဆုံးသို့ စီထားသော ဒေတာအားလုံး၏ အလယ်တန်ဖိုးဖြစ်သည်။ တစ်နည်းဆိုရသော် အလယ်အလတ်သည် သတ်မှတ်ထားသော ဒေတာများကို အညီအမျှ နှစ်ပိုင်းခွဲသည်။

ပျမ်းမျှ တွက်ချက်မှုသည် ဒေတာ စုစုပေါင်း အရေအတွက်သည် လုံးခြင်း သို့မဟုတ် ထူးဆန်းခြင်း ရှိမရှိအပေါ် မူတည်သည်-

ဒေတာစုစုပေါင်းအရေအတွက်သည် ထူးဆန်း ပါက၊ ပျမ်းမျှသည် ဒေတာ၏အလယ်တွင် ညာဘက်ကျရောက်သည့်တန်ဖိုးဖြစ်သည်။ ဆိုလိုသည်မှာ စီထားသောဒေတာ၏ အနေအထား (n+1)/2 တွင်ရှိသော တန်ဖိုးကို ဆိုလိုခြင်းဖြစ်သည်။

$Me=x_{\frac{n+1}{2}$

ဒေတာအချက်များ စုစုပေါင်းအရေအတွက်သည် တူညီ ပါက၊ အလယ်ဗဟိုတွင်ရှိသော ဒေတာအချက်နှစ်ချက်၏ ပျမ်းမျှဖြစ်လိမ့်မည်။ ဆိုလိုသည်မှာ မှာယူထားသော ဒေတာ၏ ရာထူး n/2 နှင့် n/2+1 တွင် တွေ့ရသည့် ဂဏန်းသင်္ချာပျမ်းမျှတန်ဖိုးများကို ဆိုလိုသည်။

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

ရွှေ

$n$

နမူနာရှိဒေတာစုစုပေါင်းအရေအတွက်ဖြစ်ပြီး Me သင်္ကေတသည် ပျမ်းမျှအားညွှန်ပြသည်။

➤ အလယ်အလတ်ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ဖက်ရှင်

စာရင်းဇယားများတွင်၊ မုဒ် သည် အမြင့်ဆုံး ပကတိကြိမ်နှုန်းပါရှိသော ဒေတာအစုံတွင် တန်ဖိုးဖြစ်သည်၊ ဆိုလိုသည်မှာ မုဒ်သည် ဒေတာအတွဲတစ်ခုတွင် ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးဖြစ်သည်။

ထို့ကြောင့်၊ မုဒ်အတွက် တိကျသောဖော်မြူလာမရှိသော်လည်း၊ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏မုဒ်ကို တွက်ချက်ရန်၊ နမူနာတွင် ဒေတာဒြပ်စင်တစ်ခုစီတွင် ပေါ်လာသည့်အကြိမ်အရေအတွက်ကို ရိုးရိုးရေတွက်ပြီး ထပ်ခါတလဲလဲ အများဆုံးဒေတာသည် မုဒ်ဖြစ်လိမ့်မည်။

မုဒ်ကို စာရင်းအင်းမုဒ် သို့မဟုတ် မော်ဒယ်တန်ဖိုး ဟုလည်း ဆိုနိုင်သည်။

➤ ဖက်ရှင်ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ကွဲလွဲမှု၏ ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုများအတွက် ဖော်မြူလာများ

စံသွေဖည်

စံသွေဖည်မှု၊ စံသွေဖည်မှုဟုလည်း ခေါ်တွင်သည်၊ ဒေတာစီးရီး၏ သွေဖည်မှုများ၏ နှစ်ထပ်ကိန်းများ၏ နှစ်ထပ်ကိန်း၏ နှစ်ထပ်ကိန်းနှင့် ညီမျှသည်။

ထို့ကြောင့်၊ စံသွေဖည်မှုအတွက် ဖော်မြူလာ မှာ-

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ စံသွေဖည်ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

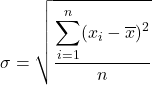
ကွဲလွဲမှု

ကွဲလွဲချက် သည် ရှုမြင်မှုစုစုပေါင်း၏ အကြွင်းအကျန်များ၏ နှစ်ထပ်ကိန်းများနှင့် ညီမျှသည်။ ထို့ကြောင့် ဤစာရင်းအင်းမက်ထရစ်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

ရွှေ-

$X$

ကွဲလွဲမှုကို သင်တွက်ချက်လိုသော ကျပန်းကိန်းရှင်ဖြစ်သည်။
$x_i$

ဒေတာတန်ဖိုး

$i$

.
$n$

လေ့လာချက် စုစုပေါင်း အရေအတွက် ဖြစ်ပါသည်။
$\overline{X}$

Random variable ၏ ဆိုလိုရင်းဖြစ်ပါသည်။

$X$

.

➤ Gap ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ကွဲလွဲမှု၏ကိန်းဂဏန်း

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ကွဲလွဲမှု၏ကိန်းဂဏန်း သည် ၎င်း၏ဆိုလိုရင်းနှင့် သက်ဆိုင်သော ဒေတာအစုတစ်ခု၏ ပြန့်ကျဲမှုကို ဆုံးဖြတ်ရန် အသုံးပြုသည့် ပြန့်ကျဲမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ကွဲလွဲမှု၏ coefficient ကို ဒေတာ၏ စံသွေဖည်မှုကို ၎င်း၏ ပျမ်းမျှအားဖြင့် ပိုင်းခြားပြီး ရာခိုင်နှုန်းတစ်ခုအဖြစ် တန်ဖိုးဖော်ပြရန် 100 ဖြင့် မြှောက်ခြင်းဖြင့် တွက်ချက်သည်။

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ ပြောင်းလဲမှုဂဏန်းတွက်စက်၏ Coefficient ကို ကြည့်ပါ။

သပ်ရပ်တယ်။

Statistical range သည် နမူနာတစ်ခုရှိ အမြင့်ဆုံးတန်ဖိုးနှင့် ဒေတာအနည်းဆုံးတန်ဖိုးအကြား ကွာခြားချက်ကို ညွှန်ပြသော ပြန့်ကျဲမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ လူဦးရေ သို့မဟုတ် စာရင်းအင်းနမူနာ၏အတိုင်းအတာကို တွက်ချက်ရန်၊ အများဆုံးတန်ဖိုးကို အနိမ့်ဆုံးတန်ဖိုးမှ နုတ်ရပါမည်။

$R=\text{M\'ax}-\text{M\'in}$

➤ ကိန်းဂဏန်းအကွာအဝေး၏ ဥပမာကို ကြည့်ပါ။

Interquartile အပိုင်းအခြား

interquartile အကွာအဝေး ( interquartile range) ဟုလည်း ခေါ်သည် ၊ သည် တတိယ နှင့် ပထမ quartiles အကြား ခြားနားချက်ကို ညွှန်ပြသော ကိန်းဂဏန်း ကွဲလွဲမှု အတိုင်းအတာ တစ်ခု ဖြစ်သည်။

ထို့ကြောင့်၊ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ interquartile အကွာအဝေးကို တွက်ချက်ရန်၊ တတိယနှင့် ပထမအကြိမ် quartiles ကို ဦးစွာရှာပြီးနောက် ၎င်းတို့ကို နုတ်ရပါမည်။

$IQR=Q_3-Q_1$

➤- Interquartile Range Calculator ကို ကြည့်ပါ။

အလယ်အလတ်ကွာခြားချက်

ပျမ်းမျှသွေဖည်မှု ( mean absolute deviation ) သည် ပကတိသွေဖည်မှုများ၏ ပျမ်းမျှဖြစ်သည်။ ထို့ကြောင့် ပျမ်းမျှသွေဖည်မှုသည် ဒေတာပစ္စည်းစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားသော ဂဏန်းသင်္ချာပျမ်းမျှမှ ဒေတာပစ္စည်းတစ်ခုစီ၏ သွေဖည်မှုပေါင်းလဒ်နှင့် ညီမျှသည်။

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ ပျမ်းမျှသွေဖည်ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ကိန်းဂဏန်းအနေအထားတိုင်းတာခြင်းအတွက် ဖော်မြူလာများ

လေးပုံတစ်ပုံ

စာရင်းဇယားများတွင်၊ quartiles များသည် မှာယူထားသောဒေတာအစုအဝေးကို လေးပိုင်းအညီအမျှ ပိုင်းခြားပေးသည့် တန်ဖိုးသုံးခုဖြစ်သည်။ ထို့ကြောင့် ပထမ၊ ဒုတိယနှင့် တတိယ ကွာတားများသည် ကိန်းဂဏန်းအချက်အလက်အားလုံး၏ 25%, 50% နှင့် 75% အသီးသီး ကိုယ်စားပြုသည်။

Quartile များကို အရင်းအနှီး Q နှင့် quartile အညွှန်းကိန်းဖြင့် ကိုယ်စားပြုသည်၊ ထို့ကြောင့် ပထမ quartile သည် Q ₁ ၊ ဒုတိယ quartile သည် Q ₂ ဖြစ်ပြီး တတိယ quartile သည် Q ₃ ဖြစ်သည်။

quartile ဖော်မြူလာ မှာ-

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် quartile ၏တန်ဖိုးမဟုတ်ဘဲ quartile ၏ အနေအထားကို ပြောပြသည်။ quartile သည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော အချက်အလက်ဖြစ်လိမ့်မည်။

သို့သော် တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ရလဒ်သည် ဒဿမ ဂဏန်း ဟုတ်၊ မဟုတ် ပေါ်မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ quartile သည် အထက်ဖော်မြူလာမှ ပေးထားသည့် အနေအထားတွင်ရှိသော ဒေတာဖြစ်သည်။
ဖော်မြူလာရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ quartile တန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$Q=x_i+d\cdot (x_{i+1}-x_i)$

x _i နှင့် x _i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။

➤ Quartile Calculator ကို ကြည့်ပါ။

ဆုံးဖြတ်ချက်များ

စာရင်းဇယားများတွင်၊ deciles များသည် မှာယူထားသောဒေတာအစုအဝေးကို ဆယ်ပိုင်းအညီအမျှ ပိုင်းခြားသည့် တန်ဖိုးကိုးခုဖြစ်သည်။ ထို့ကြောင့် ပထမ၊ ဒုတိယ၊ တတိယ၊… decile သည် နမူနာ သို့မဟုတ် လူဦးရေ၏ 10%, 20%, 30%,… ကိုကိုယ်စားပြုသည်။

Decile များကို စာလုံးအကြီး D နှင့် decile index ၊ ဆိုလိုသည်မှာ ပထမ decile သည် D ₁ ဖြစ်ပြီး ဒုတိယ decile သည် D ₂ ၊ တတိယ decile သည် D ₃ စသည်တို့ဖြစ်သည်။

Decile ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် decile ၏တန်ဖိုးမဟုတ်ဘဲ decile ၏ အနေအထားကို ပြောပြသည်။ decile သည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော ဒေတာဖြစ်လိမ့်မည်။

သို့သော်၊ တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်၊ ထို့ကြောင့် ရလဒ်သည် ဒဿမကိန်းဖြစ်ခြင်း ရှိ၊ မရှိအပေါ် မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ Decile သည် အထက်ဖော်ပြပါပုံသေနည်းမှ ပေးထားသည့် အနေအထားတွင်ရှိသော ဒေတာဖြစ်သည်။
ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ decile တန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$D=x_i+d\cdot (x_{i+1}-x_i)$

➤ Decile ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ရာခိုင်နှုန်းများ

ကိန်းဂဏန်းစာရင်းဇယားများတွင် ရာခိုင်နှုန်းများ ဆိုသည်မှာ မှာယူထားသောဒေတာအစုအဝေးကို အပိုင်းတစ်ရာစီခွဲထားသော တန်ဖိုးများဖြစ်သည်။ ထို့ကြောင့်၊ ရာခိုင်နှုန်းတစ်ခုသည် ဒေတာအစုတစ်ခု၏ ရာခိုင်နှုန်းတစ်ခုကျနေသည့် အောက်တန်ဖိုးကို ညွှန်ပြသည်။

Percentile များကို စာလုံးကြီး P ဖြင့် ကိုယ်စားပြုပြီး ရာခိုင်နှုန်းအညွှန်းကိန်း၊ ဆိုလိုသည်မှာ ပထမရာခိုင်နှုန်းသည် P _1၊ 40th ရာခိုင်နှုန်းသည် P _40၊ 79th percentile သည် P ₇₉ စသည်တို့ဖြစ်သည်။

ရာခိုင်နှုန်းပုံသေနည်း မှာ-

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် ကျွန်ုပ်တို့အား ရာခိုင်နှုန်းအလိုက် အနေအထားကို ပြောပြသည်၊ သို့သော် ၎င်း၏တန်ဖိုးကို မဟုတ်ပါ။ ရာခိုင်နှုန်းသည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော အချက်အလက်ဖြစ်လိမ့်မည်။

သို့သော်၊ တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်၊ ထို့ကြောင့် ရလဒ်သည် ဒဿမ နံပါတ်ဟုတ်မဟုတ်ပေါ်မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ ရာခိုင်နှုန်းသည် အထက်ဖော်မြူလာမှပေးဆောင်သည့် အနေအထားရှိ ဒေတာနှင့် ကိုက်ညီပါသည်။
ဖော်မြူလာရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ အတိအကျ ရာခိုင်နှုန်းတန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$P=x_i+d\cdot (x_{i+1}-x_i)$

x _i နှင့် x _i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ကိန်းဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။

➤ Percentile Calculator ကို ကြည့်ပါ။

ကိန်းဂဏန်း ပုံသဏ္ဍာန် တိုင်းတာခြင်း ဖော်မြူလာများ

asymmetry coefficient

skewness coefficient, သို့မဟုတ် skewness index, သည် ဖြန့်ဖြူးမှုတစ်ခု၏ skewness ကိုဆုံးဖြတ်ရန်အသုံးပြုသည့် ကိန်းဂဏန်းကိန်းဂဏန်းကိန်းဂဏန်းတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ asymmetry coefficient ကို တွက်ချက်ခြင်းဖြင့်၊ ၎င်းကို graphical ကိုယ်စားပြုမှု ပြုလုပ်ရန် မလိုအပ်ဘဲ ဖြန့်ဖြူးမှု၏ မညီမျှမှု အမျိုးအစားကို သိနိုင်သည်။

asymmetry coefficient အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်း ဖြစ်သည်။

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Fisher asymmetry coefficient ကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဖော်မြူလာနှစ်ခုမှ နှစ်ခုလုံးကို ညီမျှစွာအသုံးပြုနိုင်သည်-

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

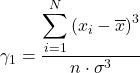
ရွှေ

$E$

သင်္ချာမျှော်လင့်ချက်၊

$\overline{x}$

ဂဏန်းသင်္ချာဆိုလို၊

$\sigma$

စံသွေဖည်မှုနှင့်

$n$

စုစုပေါင်းဒေတာ။

➤- Asymmetry coefficient ကို ကြည့်ပါ။

kurtosis ကိန်းဂဏန်း

စူးရှမှုဟုလည်း ခေါ်သော Kurtosis သည် ဖြန့်ဖြူးမှု၏ ပျမ်းမျှဝန်းကျင်တွင် မည်မျှ စုစည်းထားသည်ကို ဖော်ပြသည်။ တစ်နည်းဆိုရသော် ဖြန့်ချီမှုသည် မတ်စောက်ခြင်း သို့မဟုတ် ပြားခြင်းရှိမရှိ kurtosis ညွှန်ပြသည်။ အထူးသဖြင့်၊ ဖြန့်ဖြူးမှု၏ kurtosis ပိုကြီးလေ၊ ၎င်းသည် ပို၍ မတ်စောက်သည် (သို့မဟုတ်) ပိုပြတ်သားသည်။

kurtosis coefficient အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်း ဖြစ်သည်။

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

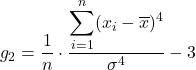
ရွှေ

$x_i$

စူးစမ်းလေ့လာခြင်းနဲ့ သက်ဆိုင်တဲ့ တန်ဖိုးဖြစ်ပါတယ်။

$i$

၊

$\overline{x}$

ဂဏန်းသင်္ချာဆိုလို၊

$\sigma$

စံသွေဖည်မှုနှင့်

$n$

စုစုပေါင်းဒေတာ။

➤- Flattening Coefficient Calculator ကို ကြည့်ပါ။

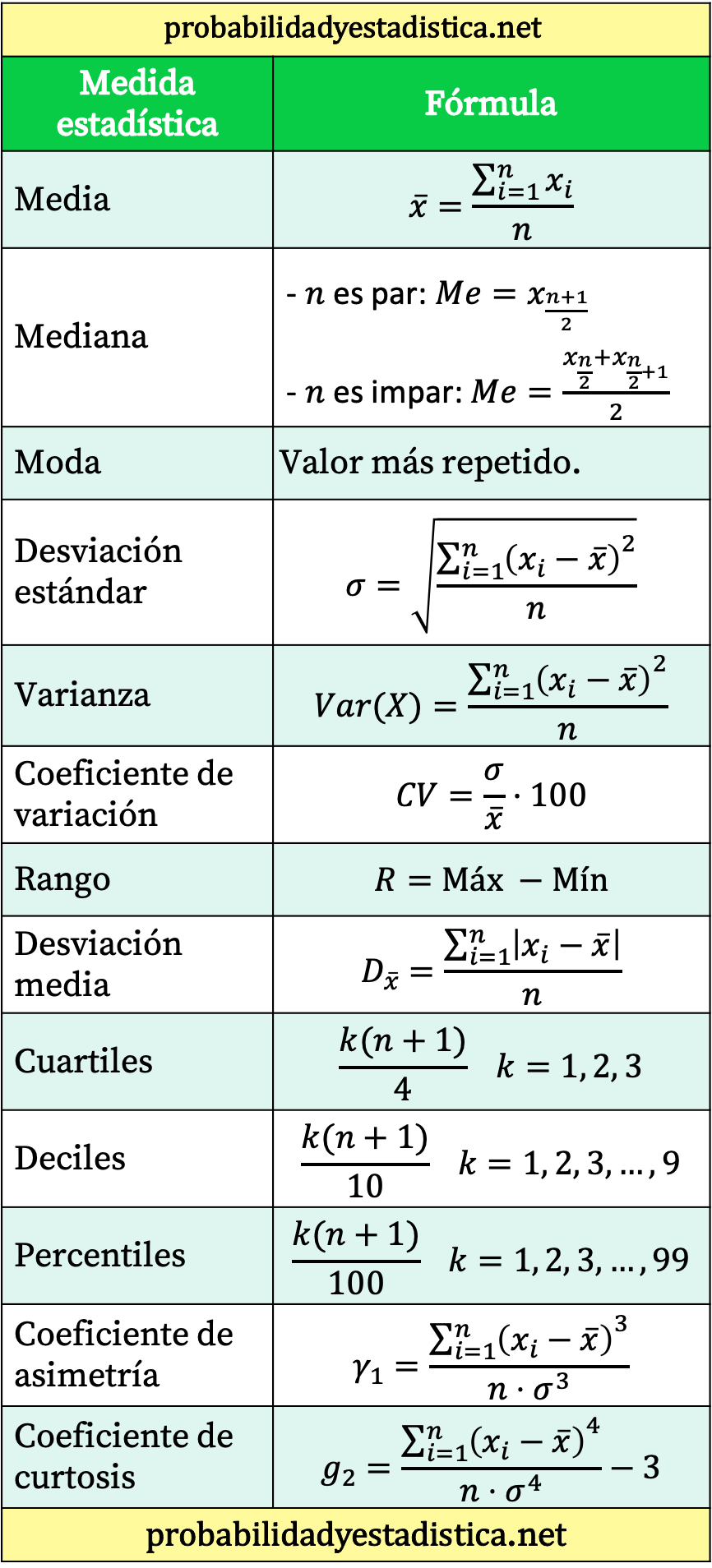
စာရင်းအင်းဖော်မြူလာအားလုံး၏ အကျဉ်းချုပ်ဇယား

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် သင့်အား ပင်မစာရင်းအင်းဖော်မြူလာများကို အကျဉ်းချုပ်ဖော်ပြသော ဇယားတစ်ခုထားခဲ့သည်။

➤ ဖြစ်နိုင်ခြေ ဖော်မြူလာများကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ဗဟိုသဘောထား၏ ကိန်းဂဏန်းတိုင်းတာမှုများအတွက် ဖော်မြူလာများ

တစ်ဝက်

မီဒီယံ

ဖက်ရှင်

ကွဲလွဲမှု၏ ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုများအတွက် ဖော်မြူလာများ

စံသွေဖည်

ကွဲလွဲမှု

ကွဲလွဲမှု၏ကိန်းဂဏန်း

သပ်ရပ်တယ်။

Interquartile အပိုင်းအခြား

အလယ်အလတ်ကွာခြားချက်

ကိန်းဂဏန်းအနေအထားတိုင်းတာခြင်းအတွက် ဖော်မြူလာများ

လေးပုံတစ်ပုံ

ဆုံးဖြတ်ချက်များ

ရာခိုင်နှုန်းများ

ကိန်းဂဏန်း ပုံသဏ္ဍာန် တိုင်းတာခြင်း ဖော်မြူလာများ

asymmetry coefficient

kurtosis ကိန်းဂဏန်း

စာရင်းအင်းဖော်မြူလာအားလုံး၏ အကျဉ်းချုပ်ဇယား

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။