စမ်းသပ်မှုဖြစ်နိုင်ခြေ

ဤတွင် စမ်းသပ်ဖြစ်နိုင်ခြေ၏ အဓိပ္ပါယ်နှင့် စမ်းသပ်ဖြစ်နိုင်ခြေကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ စမ်းသပ်ဖြစ်နိုင်ခြေကို တွက်ချက်ခြင်း၏ အဆင့်ဆင့်ဖြေရှင်းထားသော ဥပမာကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။

စမ်းသပ်မှုဖြစ်နိုင်ခြေကဘာလဲ။

Experimental probability သည် စမ်းသပ်မှုတစ်ခု၏ ရလဒ်များ သို့မဟုတ် လက်တွေ့ကျသော အချက်အလက်များအပေါ်အခြေခံ၍ ကိန်းဂဏန်းတိုင်းတာချက်တစ်ခုဖြစ်ပြီး ဖြစ်ရပ်တစ်ခုဖြစ်ပွားနိုင်ခြေကို ညွှန်ပြပါသည်။

ထို့အပြင်၊ စမ်းသပ်မှုကို ထပ်ခါထပ်ခါ ပြုလုပ်လေ၊ ရရှိသော စမ်းသပ်မှု ဖြစ်နိုင်ခြေ တိကျလေလေ ဖြစ်သည်။ ထို့ကြောင့်၊ စမ်းသပ်မှု ထောင်ပေါင်းများစွာကို လျင်မြန်စွာ ပုံဖော်နိုင်သော ကွန်ပျူတာပရိုဂရမ်များကို ယေဘုယျအားဖြင့် စမ်းသပ်မှုဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် အသုံးပြုသောကြောင့် ပိုမိုကောင်းမွန်သော တိကျမှုကို ရရှိစေသည်။

စမ်းသပ်မှုဖြစ်နိုင်ခြေကို empirical probability သို့မဟုတ် frequency probability ဟုလည်း ခေါ်သည်။

စမ်းသပ်မှုဖြစ်နိုင်ခြေသည် 0 နှင့် 1 အကြားရှိ ဂဏန်းတစ်ခုဖြစ်သည်။ ယုတ္တိနည်းအားဖြင့်၊ ဖြစ်ရပ်တစ်ခု၏ စမ်းသပ်မှုဖြစ်နိုင်ခြေတန်ဖိုး ကြီးမားလေ၊ ဖြစ်ပေါ်လာနိုင်ခြေ ပိုများလေ၊ အပြန်အလှန်အားဖြင့် တန်ဖိုးသေးငယ်လေ၊ ဖြစ်ပေါ်လာနိုင်ခြေ နည်းပါးလေဖြစ်သည်။ ဖြစ်ပေါ်လာဖွယ်ရှိသည်။ သို့မဟုတ် အဖြစ်အပျက် ဖြစ်ပေါ်လာသည်။ သို့သော် စမ်းသပ်မှုဖြစ်နိုင်ခြေ၏တန်ဖိုးသည် သုညနှင့်တစ်ခုကြားတွင် အမြဲရှိနေမည်ဖြစ်သည်။

စမ်းသပ်ဖြစ်နိုင်ခြေ ဖော်မြူလာ

စမ်းသပ်မှုဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာ သည် စမ်းသပ်မှုတစ်ခုအတွင်း ဖြစ်ရပ်တစ်ခုဖြစ်ပွားသည့်အကြိမ်အရေအတွက်ဖြစ်ပြီး စမ်းသပ်မှုပြုလုပ်ခဲ့သည့် စုစုပေါင်းအကြိမ်အရေအတွက်ဖြင့် ပိုင်းခြားထားသည်။

ဥပမာအားဖြင့်၊ လူတစ်ဦးသည် ပစ်မှတ်တစ်ခုသို့ လှံ ၁၀ ချောင်းပစ်၍ အလယ်ဗဟိုတွင် လှံ ၆ ချောင်းကို ထိရန် စီမံပါက၊ ထိုလူသည် အလယ်ဗဟိုရှိ လှံတံကို ထိနိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်သည်-

စမ်းသပ်မှုဖြစ်နိုင်ခြေ ဥပမာ

စမ်းသပ်မှုဖြစ်နိုင်ခြေ၏ သင်္ချာဆိုင်ရာ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကျွန်ုပ်တို့မြင်သည်နှင့်၊ ထို့နောက် ဤဖြစ်နိုင်ခြေအမျိုးအစားအပေါ် အဆင့်ဆင့်လေ့ကျင့်ခန်းတစ်ခုကို ဖြေရှင်းပါမည်။ ရည်ရွယ်ချက်မှာ ပွဲတစ်ခု၏ စမ်းသပ်မှုဖြစ်နိုင်ခြေကို မည်ကဲ့သို့ တွက်ချက်သည်ကို လေ့လာရန်ဖြစ်ပြီး သင့်တွင် မေးခွန်းများရှိပါက ၎င်းတို့ကို မှတ်ချက်များတွင် ရေးထားနိုင်ပါသည်။

• သေခြင်းကို လှိမ့်ခြင်း၏ ကျပန်းစမ်းသပ်မှုတွင် ပါဝင်သည့် မူလတန်းဖြစ်ရပ်များ၏ စမ်းသပ်ဖြစ်နိုင်ခြေကို တွက်ချက်ပါ။

စမ်းသပ်မှုဖြစ်နိုင်ခြေကို မရှာဖွေမီ၊ ရရှိလာသော စမ်းသပ်မှုရလဒ်များကို သီအိုရီရလဒ်များနှင့် နှိုင်းယှဉ်ရန် သီအိုရီဆိုင်ရာ ဖြစ်နိုင်ခြေကို တွက်ချက်ပါမည်။ သင်သိသည့်အတိုင်း၊ အသေကို လှိမ့်လိုက်သောအခါ ဖြစ်နိုင်ချေ ခြောက်ခုရှိသည် (၁၊ ၂၊ ၃၊ ၄၊ ၅ နှင့် ၆)၊ ထို့ကြောင့် မူလဖြစ်ရပ်တစ်ခုစီ၏ သီအိုရီဖြစ်နိုင်ခြေမှာ-

ဤလေ့ကျင့်ခန်းကိုဖြေရှင်းရန်၊ ကျွန်ုပ်တို့သည် သေတ္တာကို အကြိမ်များစွာ လှည့်ပတ်ကာ ရလဒ်များကို အရေးပေါ်ဇယားတွင် မှတ်တမ်းတင်ရပါမည်။ ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့သည် Excel ပရိုဂရမ်ဖြင့် simulations များကိုလုပ်ဆောင်မည်ဖြစ်သော်လည်း၊ သင်နှစ်သက်ရာပရိုဂရမ်ကို သိသိသာသာအသုံးပြုနိုင်ပါသည်။

ပထမဆုံး အကြိမ် ဆယ်ကြိမ်၊ ထို့နောက် အကြိမ်တစ်ရာ နှင့် နောက်ဆုံး အကြိမ် တစ်ထောင်ကို အတုလုပ်ပါမည်။ ဤနည်းဖြင့် ကျွန်ုပ်တို့သည် ရလဒ်များကို ပိုင်းခြားစိတ်ဖြာနိုင်ပြီး စမ်းသပ်မှု၏နမူနာအရွယ်အစားပေါ်မူတည်၍ ၎င်းတို့မည်သို့ပြောင်းလဲသည်ကို ကြည့်ရှုနိုင်မည်ဖြစ်သည်။ အန်စာတုံး ၁၀ ကြိမ် ကျပန်း ပုံဖော်ပြီးနောက် ရရှိသော ရလဒ်များမှာ အောက်ပါအတိုင်း ဖြစ်သည်။

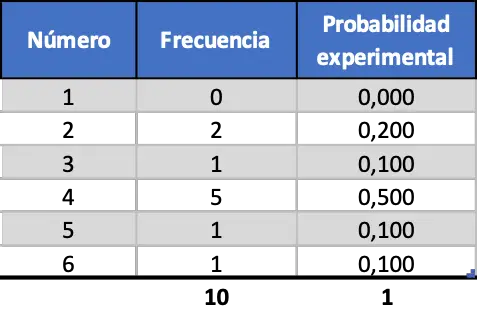
သင်တွေ့မြင်ရသည့်အတိုင်း၊ လက်ရှိရရှိသော စမ်းသပ်မှုဖြစ်နိုင်ခြေများသည် ယခင်က တွက်ချက်ထားသော သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေများ (0.167) နှင့် အတော်လေးကွာခြားပါသည်။

သို့သော် ကျွန်ုပ်တို့သည် စမ်းသပ်မှုအရေအတွက်ကို တိုးလာသည်နှင့်အမျှ၊ ဤမက်ထရစ်နှစ်ခုသည် ပို၍ဆင်တူလာသည်၊ လွှတ်တင်မှု 100 ၏ သရုပ်ဖော်ပုံကိုကြည့်ပါ-

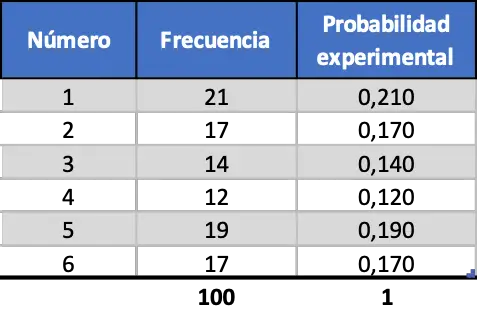
ယခု စမ်းသပ်မှုဖြစ်နိုင်ခြေသည် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေတန်ဖိုးနှင့် ပို၍တူသော်လည်း၊ ကျွန်ုပ်တို့သည် ဝေးကွာသောတန်ဖိုးများကို ရရှိဆဲဖြစ်သည်။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် တူညီသောလုပ်ထုံးလုပ်နည်းကို လုပ်ဆောင်သော်လည်း လွှတ်တင်မှုပေါင်း ၁၀၀၀ ကို ပုံဖော်ထားသည်။

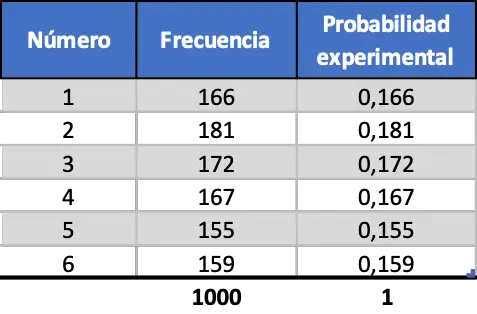
နောက်ဆုံးအခြေအနေဇယားတွင် သင်တွေ့မြင်ရသည့်အတိုင်း ယခုစမ်းသပ်မှုဖြစ်နိုင်ခြေများ၏တန်ဖိုးများသည် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေများနှင့် အလွန်ဆင်တူပါသည်။

အချုပ်အားဖြင့်၊ စမ်းသပ်မှုအရေအတွက် ပိုများလေ၊ ဖြစ်ရပ်တစ်ခု၏ စမ်းသပ်မှုဖြစ်နိုင်ခြေတန်ဖိုးသည် ၎င်း၏သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေနှင့် နီးစပ်လေဖြစ်သည်။ ဤစည်းမျဉ်းကို ကိန်းဂဏန်းများစွာ၏ ဥပဒေအဖြစ် သတ်မှတ်သည်၊ ဒေတာများများရှိလေ၊ စမ်းသပ်မှုတန်ဖိုးများသည် သီအိုရီတန်ဖိုးများနှင့် နီးကပ်လေလေဖြစ်ကြောင်း ဖော်ပြထားသည်။

အလားတူ၊ သင်သည် ကြိမ်နှုန်းဇယားသုံးခုကို နှိုင်းယှဉ်ပါက၊ စမ်းသပ်မှုဖြစ်နိုင်ခြေသည် အတိအကျမဟုတ်သော်လည်း ပြုလုပ်ခဲ့သည့် စမ်းသပ်မှုအရေအတွက်ပေါ် မူတည်၍ ပြောင်းလဲလာသည်ကို သင်တွေ့လိမ့်မည်။ ဆိုလိုချင်တာက သင်ရရှိထားတဲ့ တန်ဖိုးတွေကို ဘယ်လိုအဓိပ္ပာယ်ကောက်ရမယ်ဆိုတာ သိရပါမယ်။

စမ်းသပ်မှုဖြစ်နိုင်ခြေနှင့် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ

စမ်းသပ်မှုဖြစ်နိုင်ခြေနှင့် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ (သို့မဟုတ် ရှေးရိုးဖြစ်နိုင်ခြေ) အကြား ခြားနားချက် မှာ လက်တွေ့စမ်းသပ်မှုတစ်ခုမှ စုဆောင်းရရှိထားသော ဒေတာများမှ စမ်းသပ်မှုဖြစ်နိုင်ခြေကို တွက်ချက်ပြီး သီအိုရီဆိုင်ရာ ဖြစ်နိုင်ခြေကို မည်သည့်စမ်းသပ်မှုပြုလုပ်ရန် မလိုအပ်ဘဲ တွက်ချက်ပေးပါသည်။

ကျွန်ုပ်တို့တွေ့မြင်ခဲ့ရသည့်အတိုင်း၊ ဖြစ်ရပ်တစ်ခု၏ စမ်းသပ်မှုဖြစ်နိုင်ခြေကို တွက်ဆရန် များစွာသောစမ်းသပ်မှုများကို တုပရပါမည်။ သို့သော် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေကို တွက်ချက်ခြင်းသည် သီအိုရီနှင့် ယုတ္တိဗေဒတို့နှင့် ဆက်စပ်နေသည်။ ၎င်းကို ဤနေရာတွင် ကြည့်ရှုနိုင်သည်-