Sas တွင် scheffe စာမေးပွဲကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA ဇယား၏ စုစုပေါင်း p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ အနည်းဆုံး အုပ်စု၏ ဆိုလိုရင်းမှာ အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။

ဘယ်အဖွဲ့တွေက တစ်ခုနဲ့တစ်ခု မတူဘူးဆိုတာ အတိအကျသိဖို့အတွက် post hoc test လုပ်ဖို့လိုပါတယ်။

အသုံးအများဆုံး post hoc စာမေးပွဲများထဲမှ တစ်ခုသည် မိသားစုအလိုက် အမှားအယွင်းနှုန်းကို ထိန်းချုပ်နေစဉ် အုပ်စုတစ်ခုစီ၏ နည်းလမ်းများကြားတွင် အတွဲလိုက် နှိုင်းယှဉ်မှုများ ပြုလုပ်နိုင်စေသည့် Scheffe test ဖြစ်သည်။

အောက်ပါဥပမာသည် R တွင် Scheffe စာမေးပွဲကိုမည်သို့လုပ်ဆောင်ရမည်ကိုပြသထားသည်။

ဥပမာ- SAS တွင် Scheffe စမ်းသပ်မှု

သုတေသီတစ်ဦးသည် လေ့လာမှုတစ်ခုတွင် ပါဝင်ရန် ကျောင်းသား 30 ကို ခေါ်ယူသည်ဆိုပါစို့။ ကျောင်းသားများကို စာမေးပွဲအတွက် ပြင်ဆင်ရန် လေ့လာမှုနည်းလမ်း သုံးခုအနက်မှ တစ်ခုကို အသုံးပြုရန် ကျပန်းသတ်မှတ်ထားသည် ။

SAS တွင် ဤဒေတာအတွဲကို ဖန်တီးရန် အောက်ပါကုဒ်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;

ထို့နောက် တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ရန် proc ANOVA ကို အသုံးပြုပါမည်။

 /*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;

မှတ်ချက် – တစ်ကြောင်းတစ်ကြောင်း ANOVA မှ စုစုပေါင်း p-value သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါက Scheffe post-hoc စာမေးပွဲကို (ယုံကြည်မှုရှိသော ကြားကာလများနှင့်အတူ ) သတ်မှတ်ရန် Scheffe နှင့် Cldiff ရွေးချယ်မှုများနှင့်အတူ အဓိပ္ပါယ်ဖော်ပြချက်ကို ကျွန်ုပ်တို့အသုံးပြုထားပါသည်။

ပထမဦးစွာ ကျွန်ုပ်တို့သည် ရလဒ်တွင် ANOVA ဇယားကို ပိုင်းခြားစိတ်ဖြာပါမည်။

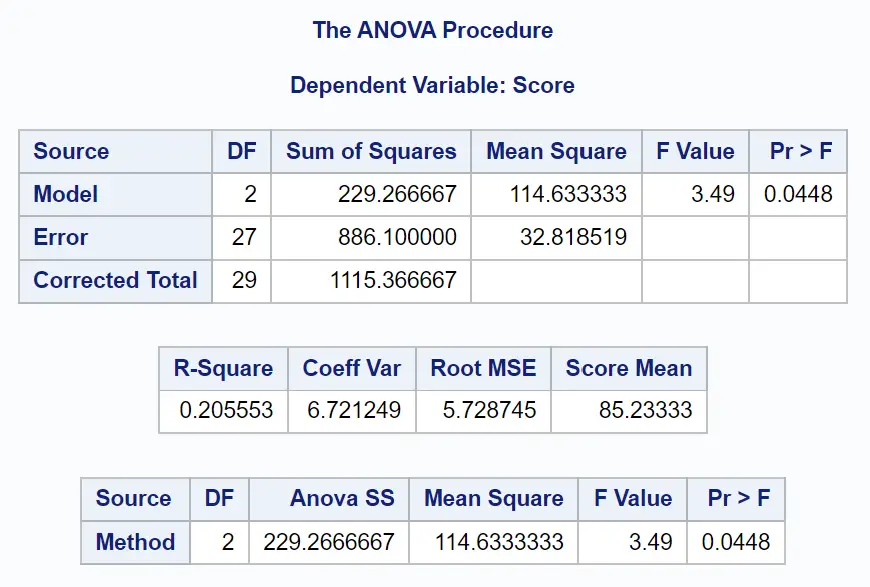
ဤဇယားမှ ကျွန်ုပ်တို့ မြင်နိုင်သည်-

• စုစုပေါင်း F-တန်ဖိုး- 3.49
• သက်ဆိုင်ရာ p-တန်ဖိုး- 0.0448

တစ်လမ်းသွား ANOVA သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုကြောင်း သတိရပါ။

• H ₀ : အုပ်စုဟူသည် အားလုံး ညီတူညီမျှဖြစ်သည်။
• H _A : အနည်းဆုံး အုပ်စုတစ်ခု၏ ပျမ်းမျှသည် မတူညီပါ။   အနားယူပါ။

ANOVA ဇယား၏ p-တန်ဖိုး (0.0448) သည် α = 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။

၎င်းသည် လေ့လာမှုနည်းလမ်းသုံးခုတွင် ပျမ်းမျှစာမေးပွဲရမှတ်သည် မညီမျှကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ဆက်စပ်- ANOVA တွင် F-Value နှင့် P-Value ကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုမည်နည်း။

မည်သည့်အုပ်စု၏ အဓိပ္ပါယ်သည် ကွဲပြားသည်ကို အတိအကျ ဆုံးဖြတ်ရန်၊ Scheffe ၏ post-hoc စာမေးပွဲများ၏ ရလဒ်များကို ပြသသည့် နောက်ဆုံးရလဒ်ဇယားကို ကိုးကားရန် လိုအပ်သည်-

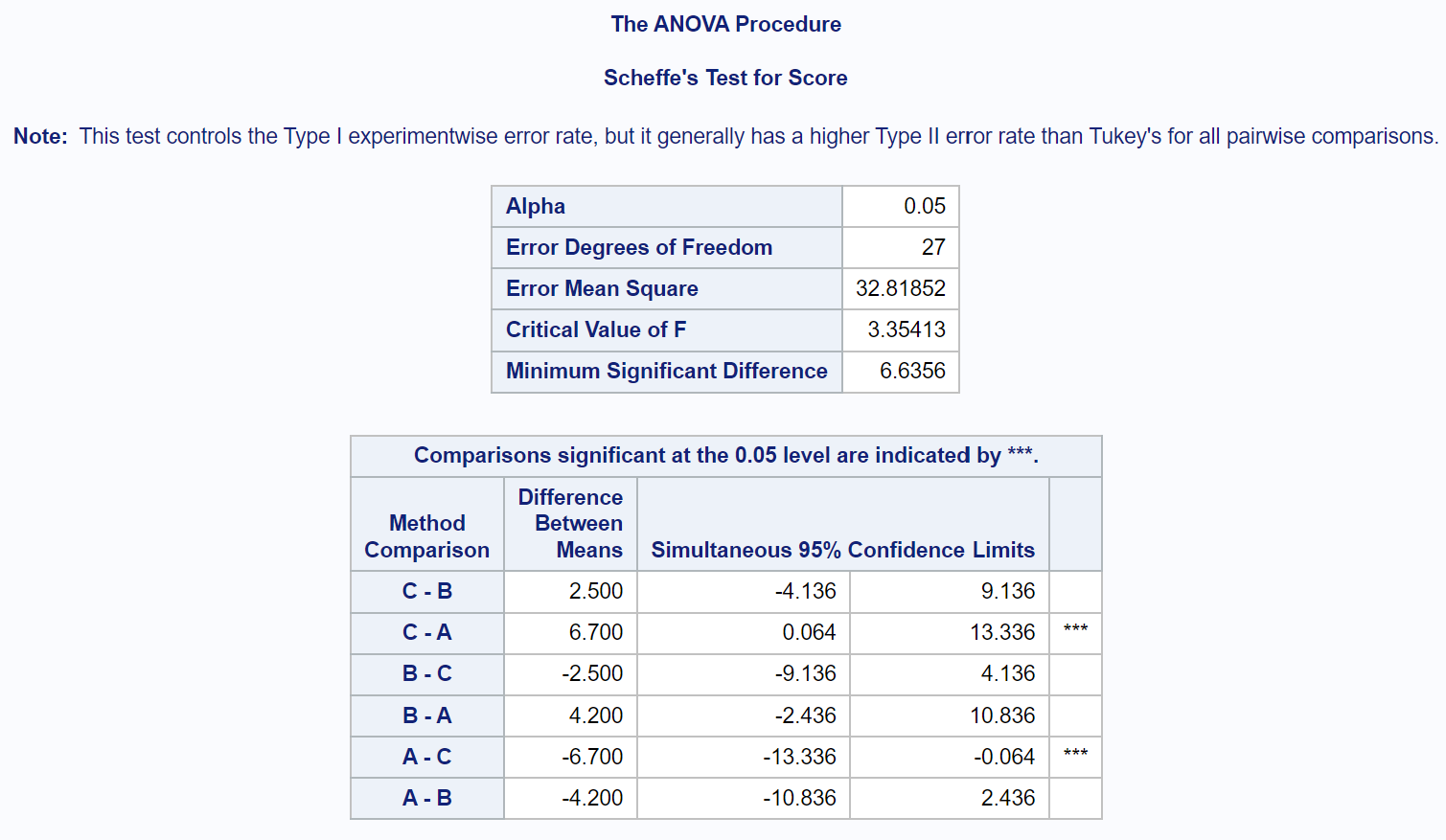
ဘယ်အဖွဲ့ရဲ့ အဓိပ္ပါယ်က ကွာခြားလဲဆိုတာကို သိချင်ရင် သူတို့ဘေးမှာ ကြယ်တွေ ( *** ) ပါနေတဲ့ အတွဲလိုက် နှိုင်းယှဉ်မှုတွေကို ကြည့်ဖို့ လိုပါတယ်။

Group A နှင့် Group C အကြား ပျမ်းမျှ စာမေးပွဲရမှတ်များတွင် ကိန်းဂဏန်း သိသိသာသာ ကွာခြားချက်ရှိကြောင်း ဇယားတွင် ပြသထားသည်။

အခြားအုပ်စုများ၏ နည်းလမ်းများကြားတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ကွာခြားချက်မရှိပါ။

အတိအကျအားဖြင့်၊ အုပ်စု C နှင့် အုပ်စု A အကြား စာမေးပွဲရမှတ်များတွင် ပျမ်းမျှ ကွာခြားချက်မှာ 6.7 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။

ဤအုပ်စုများအကြား ခြားနားချက်အတွက် 95% ယုံကြည်မှုကြားကာလသည် [0.064၊ 13.336] ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါသင်ခန်းစာများသည် ANOVA မော်ဒယ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ANOVA ဖြင့် Post-Hoc Testing ကိုအသုံးပြုခြင်းလမ်းညွှန်
SAS တွင် one-way ANOVA လုပ်ဆောင်နည်း
SAS တွင် နှစ်လမ်းသွား ANOVA လုပ်ဆောင်နည်း