Z-score သည် အနုတ်လက္ခဏာဖြစ်နိုင်ပါသလား။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ z-score သည် စံနှုန်း တစ်ခုမှ တန်ဖိုးတစ်ခုသွေဖည်မှုမည်မျှရှိသည်ကို ပြောပြသည်။ z-score ကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့အသုံးပြုသည်-

z = (X – μ) / σ

X သည် ကျွန်ုပ်တို့ ခွဲခြမ်းစိတ်ဖြာသော တန်ဖိုးဖြစ်ပြီး μ သည် ပျမ်းမျှဖြစ်ပြီး σ သည် စံသွေဖည်မှုဖြစ်သည်။

a z ရမှတ်သည် အပြုသဘော၊ အနှုတ် သို့မဟုတ် သုည ဖြစ်နိုင်သည်။

အပြုသဘော z ရမှတ်သည် သီးခြားတန်ဖိုးတစ်ခုသည် ပျမ်းမျှအထက်တွင်ရှိကြောင်း ညွှန်ပြသည်၊ အနုတ် z ရမှတ်သည် သီးခြားတန်ဖိုးတစ်ခုသည် ပျမ်းမျှအောက်တွင်ရှိကြောင်း ညွှန်ပြပြီး az ရမှတ်သည် သုည၏တန်ဖိုးတစ်ခုသည် ပျမ်းမျှနှင့်ညီမျှကြောင်းဖော်ပြသည်။

ဥပမာအချို့ကို ရှင်းရှင်းလင်းလင်း သိသင့်သည်။

ဥပမာများ- Z ရမှတ်ကို တွက်ချက်ခြင်း။

အပင်အုပ်စုတစ်စု၏ အမြင့် (လက်မဖြင့်) ကိုပြသသည့် အောက်ပါဒေတာအတွဲရှိသည် ဆိုကြပါစို့။

5၊ 7၊ 7၊ 8၊ 9၊ 10၊ 13၊ 17၊ 17၊ 18၊ 19၊ 19၊ 20

ဤဒေတာအတွဲ၏နမူနာပျမ်းမျှဆိုလိုသည်မှာ 13 ဖြစ်ပြီး နမူနာစံသွေဖည်မှုသည် 5.51 ဖြစ်သည်။

1. ဤဒေတာအတွဲတွင် “8” တန်ဖိုးအတွက် z-ရမှတ်ကို ရှာပါ။

ဤတွင် z-score တွက်ချက်နည်း။

z = (X – μ) / σ = (8 – 13) / 5.51 = -0.91၊

ဆိုလိုသည်မှာ “8” တန်ဖိုးသည် ပျမ်းမျှထက် 0.91 စံသွေဖည်မှု နိမ့် သည်ဟု ဆိုလိုသည်။

2. ဤဒေတာအတွဲတွင် “13” တန်ဖိုးအတွက် z-ရမှတ်ကို ရှာပါ။

ဤတွင် z-score တွက်ချက်နည်း။

z = (X – μ) / σ = (13 – 13) / 5.46 = 0၊

ဆိုလိုသည်မှာ “ 13” တန်ဖိုးသည် ပျမ်းမျှနှင့် အတိအကျတူညီပါသည်။

3. ဤဒေတာအတွဲတွင် “20” တန်ဖိုးအတွက် z-ရမှတ်ကို ရှာပါ။

ဤတွင် z-score တွက်ချက်နည်း။

z = (X – μ) / σ = (20 – 13) / 5.46 = 1.28

ဆိုလိုသည်မှာ “20” တန်ဖိုးသည် ပျမ်းမျှ ထက် 1.28 စံသွေဖည်မှုများဖြစ်သည်။

Z ရမှတ်များကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံ

AZ ဇယားသည် အချို့သော Z ရမှတ်များအောက် ကျရောက်သည့် တန်ဖိုးများ၏ ရာခိုင်နှုန်းကို ပြောပြသည်။ ဥပမာအချို့ကို ရှင်းရှင်းလင်းလင်း သိသင့်သည်။

ဥပမာ 1- အနုတ် Z ရမှတ်များ

ကျွန်ုပ်တို့၏ဒေတာအတွဲရှိ ကုန်ကြမ်းတန်ဖိုး “ 8” တွင် z-score သည် -0.91 ရှိသည်ကို အစောပိုင်းက တွေ့ရှိခဲ့သည်။ Z ဇယားအရ၊ တန်ဖိုးများ၏ 18.14% သည် ဤတန်ဖိုးထက်နိမ့်သည်။

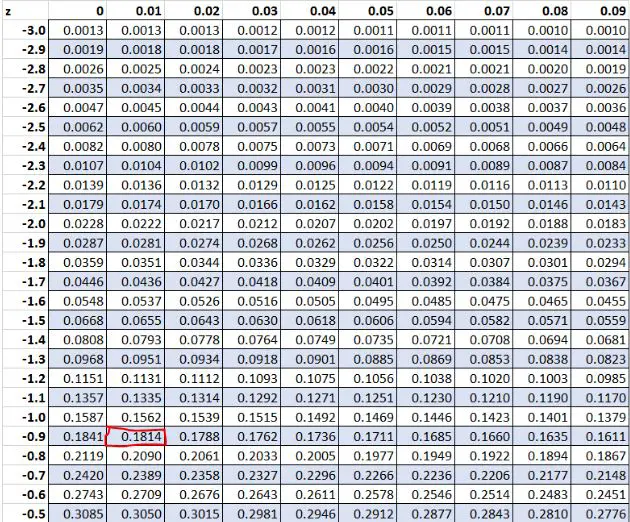
ဥပမာ 2- Z-ရမှတ်များသည် သုညနှင့်ညီသည်။

ကျွန်ုပ်တို့၏ဒေတာအတွဲရှိ ကုန်ကြမ်းတန်ဖိုး “ 13” တွင် z -score ရှိကြောင်း အစောပိုင်းတွင် ကျွန်ုပ်တို့တွေ့ရှိခဲ့သည်။ Z ဇယားအရ၊ တန်ဖိုးများ၏ 50.00% သည် ဤတန်ဖိုးထက်နည်းပါသည်။

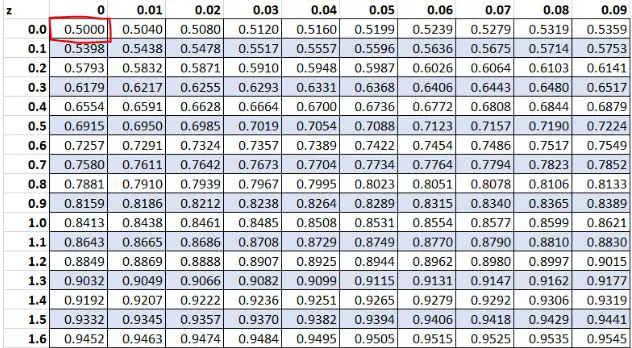
ဥပမာ 3- Positive Z ရမှတ်များ

ကျွန်ုပ်တို့၏ဒေတာအတွဲရှိ ကုန်ကြမ်းတန်ဖိုး “ 20” တွင် z-score 1.28 ရှိသည်ကို အစောပိုင်းက တွေ့ရှိခဲ့သည်။ Z ဇယားအရ၊ တန်ဖိုးများ၏ 89.97% သည် ဤတန်ဖိုးထက်နိမ့်သည်။

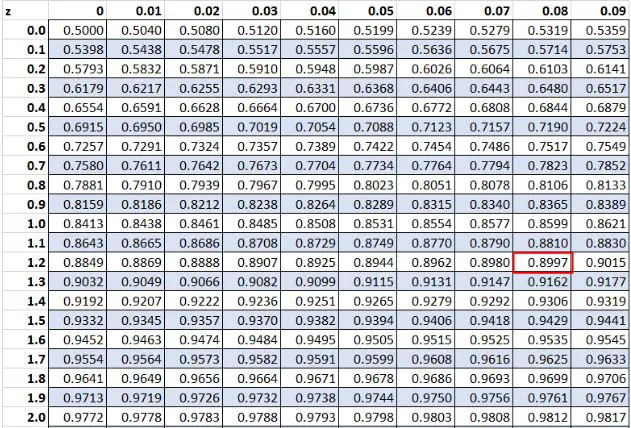
နိဂုံး

Z ရမှတ်များသည် အနုတ်လက္ခဏာ အဆုံးမရှိနှင့် အပြုသဘောဆောင်သော အဆုံးမရှိကြားရှိ မည်သည့်တန်ဖိုးကိုမဆို ယူနိုင်သော်လည်း z ရမှတ်အများစုသည် ပျမ်းမျှ၏စံသွေဖည်မှု 2 ခုအတွင်းဖြစ်သည်။ ပေးထားသော ဒေတာအတွဲအတွက် ပုံမှန်ဖြန့်ဝေမှုဖြင့် ဖော်ပြထားသည့် rule of thumb ဟုခေါ်သော ကိန်းဂဏန်းစာရင်းဇယားတွင် စည်းမျဉ်းတစ်ခု အမှန်တကယ်ရှိပါသည်။

• ဒေတာတန်ဖိုးများ၏ 68% သည် ဆိုလိုရင်း၏ စံသွေဖည်မှုတစ်ခုအတွင်းဖြစ်သည်။
• ဒေတာတန်ဖိုးများ၏ 95% သည် ဆိုလိုရင်း၏ စံသွေဖည်မှုနှစ်ခုအတွင်း ရှိပါသည်။
• ဒေတာတန်ဖိုးများ၏ 99.7% သည် စံသွေဖည်မှုသုံးမျိုးအတွင်း ကျရောက်သည်။

z-score ၏ ပကတိတန်ဖိုး မြင့်မားလေ၊ အကြမ်းထည်တန်ဖိုးသည် ဒေတာအစု၏ ပျမ်းမျှတန်ဖိုးမှ ဖြစ်သည်။ z-score ၏ ပကတိတန်ဖိုး နိမ့်လေ၊ ကုန်ကြမ်းတန်ဖိုးသည် ဒေတာအစု၏ ဆိုလိုရင်းနှင့် နီးကပ်လေဖြစ်သည်။

ဆက်စပ်အကြောင်းအရာများ-

လက်မဂဏန်းတွက်စက်၏စည်းမျဉ်းများ
Excel တွင် လက်မ၏ စည်းကမ်းကို မည်သို့ကျင့်သုံးမည်နည်း။