Excel တွင် conditional probability တွက်ချက်နည်း

အဆိုပါ ဖြစ်ရပ် B ဖြစ်ပေါ်လာခြင်းကြောင့် ဖြစ်ရပ် A ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေ ကို အောက်ပါအတိုင်း တွက်ချက်သည်-

P(A|B) = P(A∩B) / P(B)

ရွှေ-

P(A∩B) = ဖြစ်ရပ် A နှင့် ဖြစ်ရပ် B နှစ်ခုစလုံး ဖြစ်ပွားနိုင်ခြေ။

P(B) = အဆိုပါဖြစ်ရပ် B ဖြစ်ပေါ်လာနိုင်ခြေ။

ဤဖော်မြူလာသည် အမျိုးအစားခွဲကိန်းရှင်နှစ်ခုအတွက် ကြိမ်နှုန်းများ (သို့မဟုတ် “ အရေအတွက်” ) ကိုပြသသည့် ဇယားဖြစ်သည့် နှစ်လမ်းသွားဇယားတစ်ခုအတွက် ဖြစ်နိုင်ခြေများကို တွက်ချက်ရာတွင် အထူးအသုံးဝင်ပါသည်။

ဥပမာအားဖြင့်၊ ဘေ့စ်ဘော၊ ဘတ်စကက်ဘော၊ ဘောလုံး၊ ဘောလုံး သို့မဟုတ် ဘောလုံးတို့ နှစ်သက်သော လူ ၃၀၀ ကို မေးမြန်းသော စစ်တမ်းတစ်ခု၏ ရလဒ်ကို ဥပမာအားဖြင့်၊ အောက်ပါ နှစ်လမ်းသွားဇယားက ပြသည်။ အတန်းများသည် ဖြေဆိုသူ၏ လိင်အမျိုးအစားကို ပြသထားပြီး ကော်လံများက ၎င်းတို့ရွေးချယ်သည့် အားကစားကို ညွှန်ပြသည်-

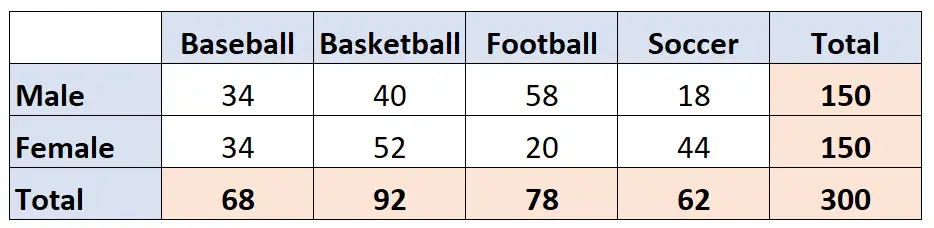
ကျွန်ုပ်တို့တွင် အမျိုးအစားခွဲခြားနိုင်သော ကွဲပြားချက် နှစ်ခု ရှိသည်ဖြစ်သောကြောင့် ကျား-မနှင့် အကြိုက်ဆုံးအားကစား။

ထို့နောက် Excel ရှိ two-way tables အတွက် conditional probability တွက်ချက်နည်းကို ပြသပါမည်။

Excel တွင် Conditional Probability တွက်ချက်နည်း

ဥပမာမေးခွန်းတွေကို ဖြေချင်တယ်ဆိုပါစို့။

“ သူအကြိုက်ဆုံး အားကစားက ဘေ့စ်ဘောလို့ ဖြေဆိုသူ အမျိုးသားက ဘယ်လောက် ဖြစ်နိုင်လဲ။” »

အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေဖော်မြူလာကို အသုံးပြု၍ အဖြေကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-

P(အမျိုးသား|ဘေ့စ်ဘော) = P(အမျိုးသား∩ဘေ့စ်ဘော) / P(ဘေ့စ်ဘော) = (34/300) / (68/300) = 0.5

ထို့ကြောင့်၊ သူအကြိုက်ဆုံးအားကစားမှာ ဘေ့စ်ဘောဖြစ်ပြီး ဖြေဆိုသူသည် အမျိုးသားဖြစ်နိုင်ခြေမှာ 0.5 (သို့မဟုတ် 50%) ဖြစ်သည်။

အလားတူ ဖော်မြူလာကို အသုံးပြု၍ ဇယားရှိ အခြားသော အခြေအနေများအတွက် အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေများကို တွက်ချက်နိုင်ပါသည်။ အောက်ဖော်ပြပါပုံသည် ဇယားရှိ အခြေအနေအလိုက် ဖြစ်နိုင်ခြေတစ်ခုစီကို အသုံးပြုထားသော ဖော်မြူလာနှင့်အတူ တွက်ချက်နည်းကို ပြသသည်-

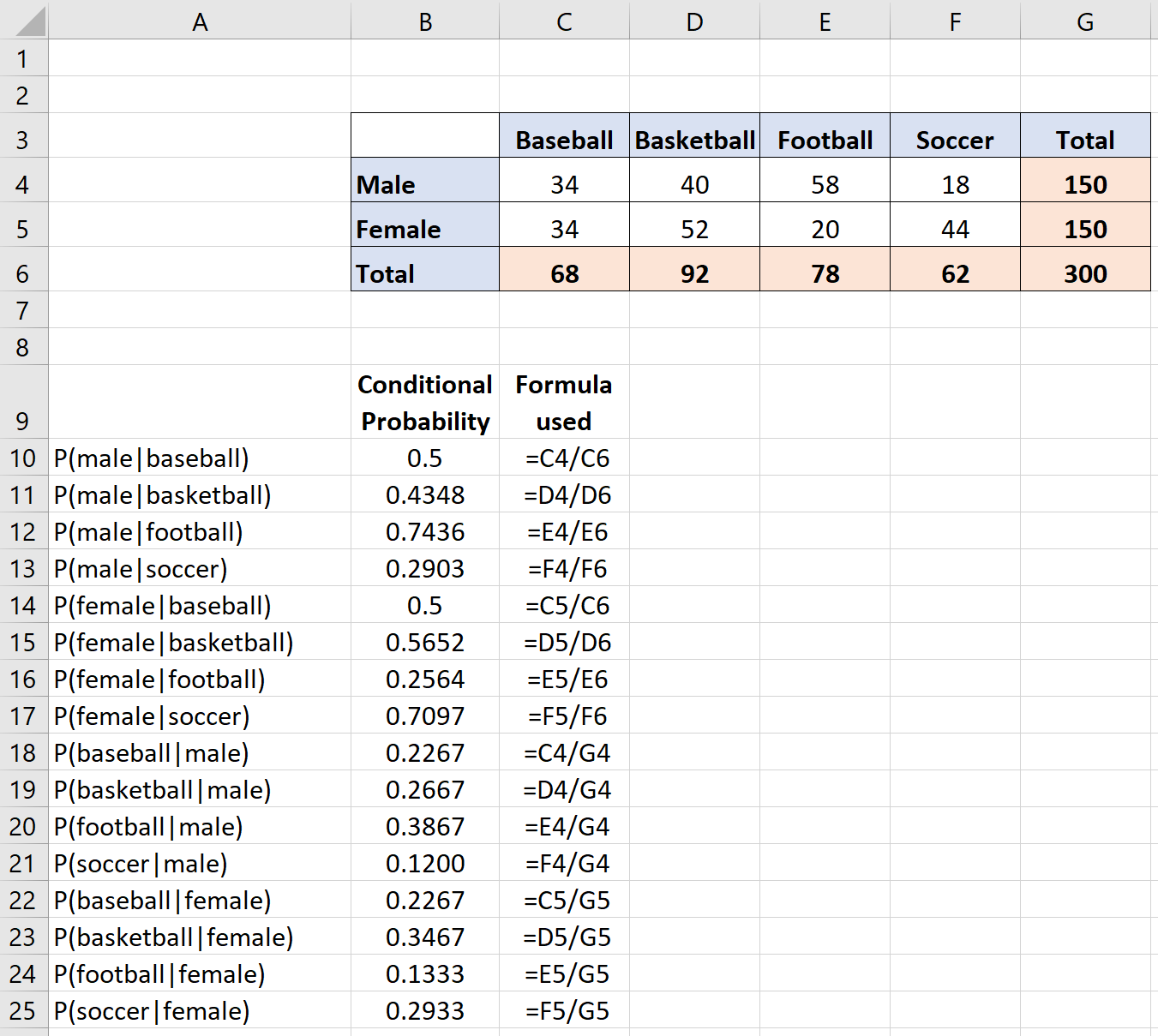
အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေတွက်ချက်မှုတစ်ခုစီအတွက်၊ ကျွန်ုပ်တို့သည် အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေဖော်မြူလာကို P(A|B) = P(A∩B) / P(B) ၏အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေဖော်မြူလာကို အသုံးပြုကြောင်း သတိပြုပါ။

ဥပမာအားဖြင့်၊ ဖြေဆိုသူ၏အကြိုက်ဆုံးအားကစားမှာ ဘောလုံးဖြစ်ပြီး၊ သူမသည် အမျိုးသမီးဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်သည်-

P(ဘောလုံး|အမျိုးသမီး) = P(ဘောလုံး∩female)/P(အမျိုးသမီး)

ဖြေဆိုသူ 300 တွင် အမျိုးသမီး 44 ဦး အတိအကျ ရှိပြီး ဘောလုံးကို ၎င်းတို့၏ အကြိုက်ဆုံး အားကစားအဖြစ် နှစ်သက်သောကြောင့် P(soccer∩female) = 44/300 ဖြစ်သည်။

ဖြေဆိုသူ ၃၀၀ တွင် အမျိုးသမီး ၁၅၀ ရှိပြီး P(အမျိုးသမီး) = 150/300 ဖြစ်သည်။

ထို့ကြောင့် P(soccer|female) = P(soccer∩female) / P(female) = (44/300) / (150/300) = 0.2933 ။

အခြေအနေတစ်ခုစီအတွက် ဖြစ်နိုင်ခြေအခြေအနေတစ်ခုစီအတွက် အလားတူတွက်ချက်မှုကို လုပ်ဆောင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

double entry table မှာ conditional relative frequency ကို ဘယ်လိုရှာမလဲ။
စာရင်းဇယားများတွင် အခြေအနေအရ ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။