နှိုင်းရကြိမ်နှုန်း ဟီစတိုဂရမ်- အဓိပ္ပါယ် + ဥပမာ
ကိန်းဂဏန်းစာရင်းဇယားများတွင် မကြာခဏဆိုသလို ကြိမ်နှုန်းများအကြောင်း အချက်အလက်ပြသသည့် ဇယားများကို သင်တွေ့လိမ့်မည်။ ကြိမ်နှုန်းများသည် အဖြစ်အပျက်တစ်ခု မည်မျှဖြစ်ပွားခဲ့သည်ကို ကျွန်ုပ်တို့အား ရိုးရှင်းစွာပြောပြပါသည်။
ဥပမာအားဖြင့်၊ အောက်ပါဇယားသည် ပစ္စည်း၏စျေးနှုန်းအပေါ်အခြေခံ၍ တစ်ပတ်အတွင်း ရောင်းချသည့်ပစ္စည်းအရေအတွက်ကို ပြသသည်-
| ပစ္စည်းစျေးနှုန်း | အကြိမ်ရေ |
|---|---|
| $1 – $10 | ၂၀ |
| $11 – $20 | ၂၁ |
| $21 – $30 | ၁၃ |
| $31 – $40 | ၈ |
| $41 – $50 | ၄ |
ဤဇယားအမျိုးအစားကို ကြိမ်နှုန်းဇယား ဟုခေါ်သည်။ ကော်လံတစ်ခုတွင် ကျွန်ုပ်တို့တွင် “အတန်း” ရှိပြီး အခြားကော်လံတွင် ကျွန်ုပ်တို့တွင် သင်တန်း၏အကြိမ်ရေရှိသည်။
ကျွန်ုပ်တို့သည် ကိန်းများကို မြင်ယောင်နိုင်သောအခါတွင် ဒေတာကို နားလည်ရန် ပိုလွယ်ကူသောကြောင့် ကြိမ်နှုန်းဇယားရှိ တန်ဖိုးများကို မြင်ယောင်ရန် ကြိမ်နှုန်းဟစ်စတိုဂရမ်များကို အသုံးပြုလေ့ရှိသည်။
ဟစ်စတိုဂရမ်တစ်ခုသည် ဂရပ်တစ်ခု၏ x ဝင်ရိုးတစ်လျှောက် အတန်းများကို စာရင်းပြုစုပြီး y ဝင်ရိုးတစ်လျှောက် အတန်းတစ်ခုစီ၏ ကြိမ်နှုန်းကို ကိုယ်စားပြုရန် ဘားများကို အသုံးပြုသည်။ အောက်ဖော်ပြပါ ကြိမ်နှုန်းဟစ်စတိုဂရမ်သည် အထက်ဖော်ပြပါ ကြိမ်နှုန်းဇယား၏ အမြင်အာရုံကို ဖော်ပြပေးသည်-
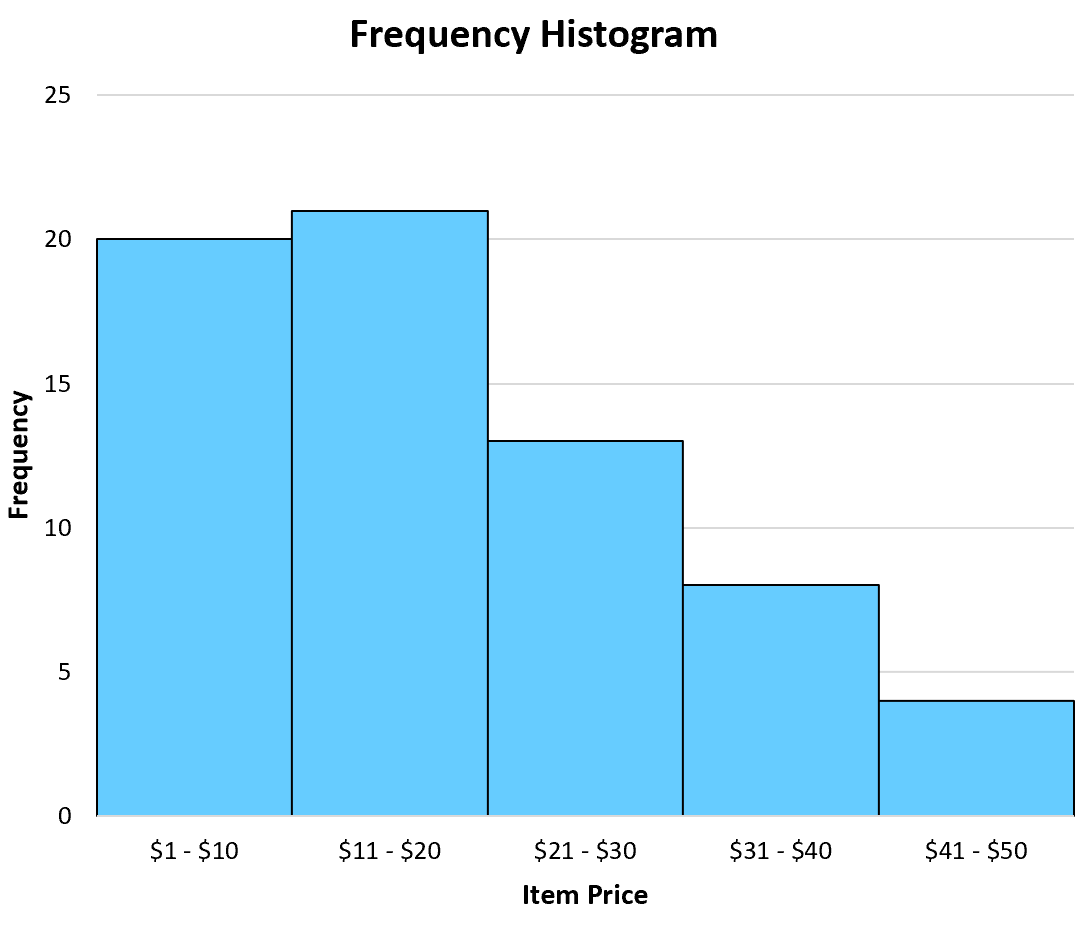
ကြိမ်နှုန်းဇယားတစ်ခု၏ ရင်းနှီးသောဝမ်းကွဲတစ်ဝမ်းကွဲသည် အတန်းအားလုံး၏ ရာခိုင်နှုန်းတစ်ခုအဖြစ် အတန်းတစ်ခုစီ၏ ကြိမ်နှုန်းများကို ရိုးရိုးရှင်းရှင်းဖော်ပြသည့် ဆွေမျိုးကြိမ်နှုန်းဇယားတစ်ခုဖြစ်သည် ။
အောက်ဖော်ပြပါဇယားသည် ယခင်က ကျွန်ုပ်တို့တွေ့မြင်ခဲ့သော တူညီသောဒေတာအစု၏ နှိုင်းရကြိမ်နှုန်းများကို ပြသသည်-
| ပစ္စည်းစျေးနှုန်း | အကြိမ်ရေ | နှိုင်းရကြိမ်နှုန်း |
|---|---|---|
| $1 – $10 | ၂၀ | ၀.၃၀၃ |
| $11 – $20 | ၂၁ | ၀.၃၁၈ |
| $21 – $30 | ၁၃ | ၀.၁၉၇ |
| $31 – $40 | ၈ | ၀.၁၂၁ |
| $41 – $50 | ၄ | ၀.၀၆၁ |
စုစုပေါင်း (၆၆) မျိုးကို ရောင်းချခဲ့သည်။ ထို့ကြောင့်၊ အတန်းတစ်ခုစီ၏ ကြိမ်နှုန်းကိုယူ၍ ရောင်းချသည့်ပစ္စည်းစုစုပေါင်းဖြင့် ပိုင်းခြားခြင်းဖြင့် အတန်းတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို တွေ့ရှိခဲ့သည်။
ဥပမာအားဖြင့်၊ ပစ္စည်း ၂၀ ကို ၁ ဒေါ်လာမှ ၁၀ ဒေါ်လာအထိ စျေးနှုန်းအကွာအဝေးဖြင့် ရောင်းချခဲ့သည်။ ထို့ကြောင့်၊ class $1 – $10 ၏ နှိုင်းရကြိမ်နှုန်းသည် 20 / 66 = 0.303 ဖြစ်သည်။
ထို့နောက် ပစ္စည်း ၂၁ မျိုးကို စျေးနှုန်း ၁၁ ဒေါ်လာမှ ဒေါ်လာ ၂၀ အတွင်း ရောင်းချခဲ့သည်။ ထို့ကြောင့် $11 – $20 အတန်း၏ နှိုင်းရကြိမ်နှုန်းသည် 21/66 = 0.318 ဖြစ်သည်။
ကျွန်ုပ်တို့သည် ဆွေမျိုးကြိမ်နှုန်းများရရှိရန် အတန်းတစ်ခုစီအတွက် တူညီသောတွက်ချက်မှုကို လုပ်ဆောင်သည်။
ကျွန်ုပ်တို့တွင် အတန်းတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို ရရှိပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် ထိုနှိုင်းရကြိမ်နှုန်းများကို မြင်သာစေရန် နှိုင်းရကြိမ်နှုန်း histogram တစ်ခုကို ဖန်တီးနိုင်သည်။
ကြိမ်နှုန်းဟစ်စတိုဂရမ်နှင့်ဆင်တူသည်၊ ဤဟစ်စတိုဂရမ်အမျိုးအစားသည် ဂရပ်၏ x-ဝင်ရိုးတစ်လျှောက် အတန်းများကိုပြသပြီး y-ဝင်ရိုးတစ်လျှောက်ရှိ အတန်းတစ်ခုစီ၏ဆွေမျိုးကြိမ်နှုန်းများကိုကိုယ်စားပြုရန် ဘားများကိုအသုံးပြုသည်။
တစ်ခုတည်းသော ကွာခြားချက်မှာ y-ဝင်ရိုးပေါ်တွင် အသုံးပြုသည့် တံဆိပ်များဖြစ်သည်။ ကြိမ်နှုန်းကြမ်းများကို ပြသမည့်အစား နှိုင်းရကြိမ်နှုန်း ဟီစတိုဂရမ်သည် ရာခိုင်နှုန်းများကို ပြသသည်။
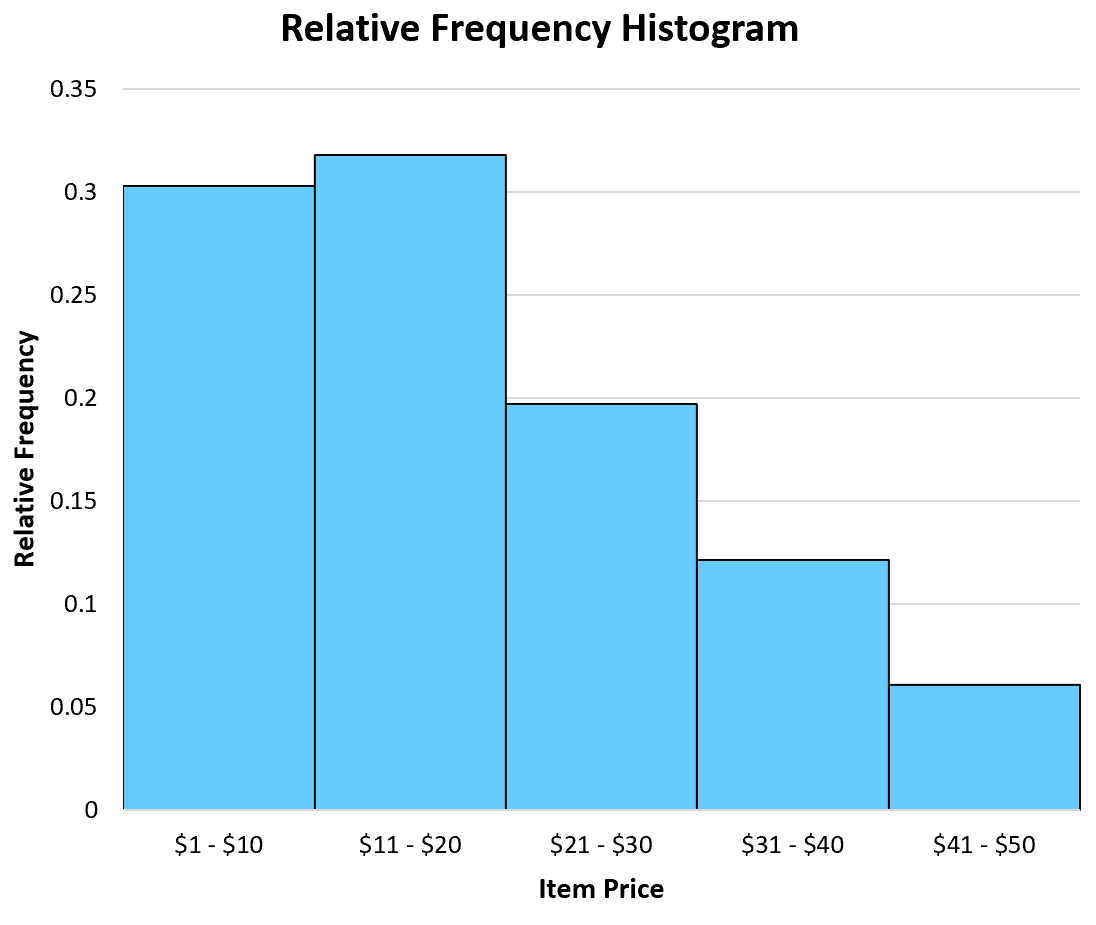
ဆွေမျိုးကြိမ်နှုန်း ဟီစတိုဂရမ်ကို ဘယ်အချိန်မှာ သုံးမလဲ။
ကုန်ကြမ်းဒေတာတန်ဖိုးများကို သင်စိတ်ဝင်စားသောအခါ ကြိမ်နှုန်း histogram သည် အသုံးဝင်နိုင်သည်။ ဥပမာအားဖြင့်၊ စတိုးဆိုင်တစ်ခုသည် $41 မှ $50 အကွာအဝေးအတွင်း တစ်ပတ်လျှင် အနည်းဆုံး ပစ္စည်း 10 ခု ရောင်းချရန် ရည်မှန်းထားသည်။
၎င်းတို့၏ဒေတာ၏ ကြိမ်နှုန်းဟစ်စတိုဂရမ်ကို ဖန်တီးခြင်းဖြင့်၊ ဤစျေးနှုန်းအကွာအဝေးတွင် တစ်ပတ်လျှင် ပစ္စည်း 10 ခုရောင်းချရန် ၎င်းတို့၏ပန်းတိုင်ကို မပြည့်မီကြောင်း အလွယ်တကူ သိနိုင်သည်-

အပြန်အလှန်အားဖြင့်၊ ရာခိုင်နှုန်းတန်ဖိုးများကို သင်စိတ်ဝင်စားသောအခါ နှိုင်းရကြိမ်နှုန်း histogram သည် အသုံးဝင်သည်။ ဥပမာအားဖြင့်၊ စတိုးဆိုင်တစ်ခုသည် ၎င်း၏စုစုပေါင်းပစ္စည်းများ၏ 5% ကို စျေးနှုန်းအကွာအဝေး $41 နှင့် $50 ကြားတွင် ရောင်းချရန် ရည်မှန်းချက်ရှိနိုင်သည်။
၎င်းတို့၏ဒေတာ၏ နှိုင်းရကြိမ်နှုန်း ဟီစတိုဂရမ်ကို ဖန်တီးခြင်းဖြင့်၊ ၎င်းတို့သည် ဤပန်းတိုင်ကို အရောက်လှမ်းနိုင်သည်ကို တွေ့မြင်နိုင်သည်-

ကြိမ်နှုန်းဟစ်စတိုဂရမ် နှင့် နှိုင်းရကြိမ်နှုန်းဟစ်စတိုဂရမ် နှစ်ခုလုံးသည် အတိအကျတူညီနေမည်ကို သတိပြုပါ။ တစ်ခုတည်းသော ခြားနားချက်မှာ y ဝင်ရိုးပေါ်တွင် ဖော်ပြထားသော တန်ဖိုးများဖြစ်သည်။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော ကိန်းဂဏန်းဆော့ဖ်ဝဲများတွင် နှိုင်းရကြိမ်နှုန်း ဟီစတိုဂရမ်များကို ဖန်တီးနည်းကို ရှင်းပြသည်-
R တွင် နှိုင်းရကြိမ်နှုန်း ဟီစတိုဂရမ် ဖန်တီးနည်း
Python တွင် Relative Frequency Histogram ဖန်တီးနည်း