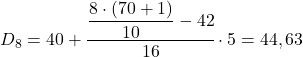Deciles

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါး၌ ကျွန်ုပ်တို့သည် စီစဥ်ပုံနှင့် တွက်ချက်ပုံကို ရှင်းပြထားပါသည်။ decile တွက်ချက်မှုများ၏ အဆင့်ဆင့်ဖြေရှင်းထားသော ဥပမာများစွာကိုလည်း သင်တွေ့နိုင်မည်ဖြစ်ပြီး ထို့အပြင်၊ အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် မည်သည့်ကိန်းဂဏန်းနမူနာ၏ deciles များကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

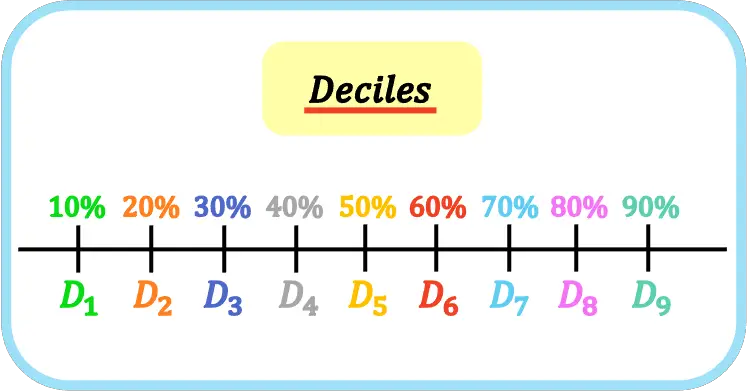
ဆုံးဖြတ်ချက်များ ဆိုသည်မှာ အဘယ်နည်း။

စာရင်းဇယားများတွင်၊ deciles များသည် မှာယူထားသောဒေတာအစုအဝေးကို ဆယ်ပိုင်းအညီအမျှ ပိုင်းခြားသည့် တန်ဖိုးကိုးခုဖြစ်သည်။ ထို့ကြောင့် ပထမ၊ ဒုတိယ၊ တတိယ၊… decile သည် နမူနာ သို့မဟုတ် လူဦးရေ၏ 10%, 20%, 30%,… ကိုကိုယ်စားပြုသည်။

ဥပမာအားဖြင့်၊ စတုတ္ထ decile တန်ဖိုးသည် ဒေတာ၏ 40% ထက် မြင့်မားသော်လည်း ကျန်ဒေတာများထက် နိမ့်သည်။

Decile များကို စာလုံးအကြီး D နှင့် decile index ၊ ဆိုလိုသည်မှာ ပထမ decile သည် D ₁ ဖြစ်ပြီး ဒုတိယ decile သည် D ₂ ၊ တတိယ decile သည် D ₃ စသည်တို့ဖြစ်သည်။

👉 မည်သည့်ဒေတာအတွဲအတွက်မဆို decis များကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

deciles များသည် quartiles၊ quintiles နှင့် percentiles များကဲ့သို့ပင် ဗဟိုအနေအထားမဟုတ်သော အတိုင်းအတာတစ်ခုဖြစ်ကြောင်း သတိပြုသင့်သည်။ ကျွန်ုပ်တို့၏ဝဘ်ဆိုဒ်တွင် ဤပမာဏအမျိုးအစားတစ်ခုစီ၏ အဓိပ္ပါယ်ကို သင်စစ်ဆေးနိုင်ပါသည်။

ထို့အပြင်၊ ပဉ္စမ decile သည် သတ်မှတ်ထားသော ဒေတာတစ်ခုလုံးကို အညီအမျှ နှစ်ပိုင်းခွဲထားသောကြောင့် ပျမ်းမျှနှင့် ဒုတိယ quartile နှင့် ညီမျှပါသည်။

စီစဥ်ပုံတွက်နည်း

ကိန်းဂဏန်းအချက်အလက်အတွဲလိုက်၏ decile အနေအထားကို တွက်ချက် ရန်၊ ကိန်းဂဏန်းကို ဒေတာစုစုပေါင်း၏ပေါင်းလဒ်နှင့် ပေါင်းထည့်ကာ ရလဒ်ကို ဆယ်ပြားဖြင့် ပိုင်းပါ။

ထို့ကြောင့် decile ဖော်မြူလာ မှာ-

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် decile ၏တန်ဖိုးမဟုတ်ဘဲ decile ၏ အနေအထားကို ပြောပြသည်။ decile သည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော ဒေတာဖြစ်လိမ့်မည်။

သို့သော်၊ တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်၊ ထို့ကြောင့် ရလဒ်သည် ဒဿမကိန်းဖြစ်ခြင်း ရှိ၊ မရှိအပေါ် မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ Decile သည် အထက်ဖော်ပြပါပုံသေနည်းမှ ပေးထားသည့် အနေအထားတွင်ရှိသော ဒေတာဖြစ်သည်။
ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ decile တန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$D=x_i+d\cdot (x_{i+1}-x_i)$

x _i နှင့် x _i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။

ကိန်းဂဏန်းနမူနာတစ်ခု၏ ဆယ်လီများကို ရယူခြင်းသည် ရှုပ်ထွေးသည်ဟု သင်ထင်ကောင်းထင်နိုင်သော်လည်း လက်တွေ့တွင်မူ အလွန်ရိုးရှင်းပါသည်။ အောက်ပါ ဥပမာနှစ်ခုကို သင်ဖတ်ပါက ၎င်းကို သင်ပိုမိုနားလည်လာမည်မှာ သေချာပါသည်။

မှတ်ချက် – သိပ္ပံပညာအသိုက်အဝန်းသည် စီစဥ်တွက်ချက်ပုံနှင့်ပတ်သက်၍ လုံးလုံးလျားလျားသဘောမတူသောကြောင့် ၎င်းကို အနည်းငယ်ကွဲပြားအောင် ရှင်းပြထားသည့် စာရင်းအင်းစာအုပ်များကို သင်ရှာတွေ့နိုင်ပါသည်။

decile တွက်ပုံဥပမာ

အထက်ဖော်ပြပါအတိုင်း သင်မြင်ခဲ့သည့်အတိုင်း၊ ဒိုင်ခွက်များ၏ တွက်ချက်မှုသည် ကျွန်ုပ်တို့အား ပထမဖော်မြူလာမှ ပေးသော ကိန်းဂဏန်းသည် ဒဿမဖြစ်မဖြစ်ပေါ်တွင် မူတည်သည်၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ ဖြေရှင်းချက်နမူနာနှစ်ခုကို ပြင်ဆင်ထားပြီး၊ ကိစ္စတစ်ခုစီအတွက် တစ်ခုစီကို ပြင်ဆင်ထားပါသည်။ မည်သို့ပင်ဆိုစေ၊ သင့်တွင် decis များ၏ဖွဲ့စည်းမှုနှင့်ပတ်သက်သည့်မေးခွန်းများရှိပါက၊ ၎င်းတို့ကို comment တွင်မေးနိုင်ကြောင်း သတိရပါ။

ဥပမာ ၁

အသေးဆုံးမှ အကြီးဆုံးအထိ အောက်ပါဒေတာများကို ပေးထားသည့်နမူနာ၏ ပထမ၊ တတိယနှင့် အဋ္ဌမမြောက် decile ကို ရှာပါ။

ဤလေ့ကျင့်ခန်းရှိ ဒေတာကို စီစစ်ပြီးဖြစ်သောကြောင့် အစဉ်လိုက်ပြောင်းရန် မလိုအပ်ပါ၊ သို့မဟုတ်ပါက ကျွန်ုပ်တို့သည် ဒေတာကို အငယ်ဆုံးမှ အကြီးဆုံးသို့ ဦးစွာစီရန် လိုအပ်ပါသည်။

အထက်တွင်ရှင်းပြထားသည့်အတိုင်း Deciles များ၏ ရာထူးများကို ရှာဖွေနိုင်စေမည့် ပုံသေနည်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

ဤလေ့ကျင့်ခန်းအတွက်နမူနာအရွယ်အစားသည် ရှုမြင်မှု 29 ဖြစ်သည်၊ ထို့ကြောင့် ပထမ decile ၏အနေအထားကိုတွက်ချက်ရန် 29 ကို n နှင့် k အတွက် 1 ကို အစားထိုးရပါမည်။

$\cfrac{1\cdot (29+1)}{10}=3\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_1=85$

ဖော်မြူလာ၏ရလဒ်သည် 3 ဖြစ်ပြီး၊ ထို့ကြောင့် ပထမ decile သည် မှာယူထားသောစာရင်း၏ တတိယနေရာ၌ ရှိနေမည်ဖြစ်ပြီး ဤတန်ဖိုးသည် 85 နှင့် သက်ဆိုင်သည်။

ယခု ကျွန်ုပ်တို့သည် တူညီသောလုပ်ထုံးလုပ်နည်းကို တဖန်တဖန် ကျင့်သုံးသော်လည်း တတိယအချက်ဖြင့် လုပ်ဆောင်ပါသည်။ ကျွန်ုပ်တို့သည် k ကို 3 ဖြင့် အစားထိုးသည့် ဖော်မြူလာကို အသုံးပြုသည်။

$\cfrac{3\cdot (29+1)}{10}=9\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_3=97$

ထို့ကြောင့် တတိယ decile သည် 97 တွင်နဝမအနေအထားရှိဒြပ်စင်ဖြစ်သည်။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် တူညီသောလုပ်ငန်းစဉ်ကိုလုပ်ဆောင်သော်လည်း အဋ္ဌမမြောက် decile ကိုဆုံးဖြတ်ရန် ဖော်မြူလာတွင် 8 ကိုထည့်ပါ။

$\cfrac{8\cdot (29+1)}{10}=24\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_8=131$

အဋ္ဌမမြောက် Decile သည် မှာယူထားသောဒေတာစာရင်း၏ အနေအထား 24 တွင် နံပါတ်ဖြစ်မည်ဖြစ်သောကြောင့် အဋ္ဌမမြောက် Decile သည် 131 ဖြစ်သည်။

ဥပမာ ၂

အောက်ပါဇယားရှိဒေတာမှ decles 4၊ 7 နှင့် 9 ကိုတွက်ချက်ပါ။

ယခင်ဥပမာတွင်အတိုင်း၊ decis များ၏ရာထူးများကိုရယူရန် အောက်ပါပုံသေနည်းကို အသုံးပြုရပါမည်။

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

ဤကိစ္စတွင်၊ နမူနာအရွယ်အစားမှာ 42 ဖြစ်ပြီး၊ ထို့ကြောင့် စတုတ္ထ decile ၏ အနေအထားကိုရှာဖွေရန် parameter n ကို 42 နှင့် k ဖြင့် 4 ဖြင့် အစားထိုးရပါမည်။

$\cfrac{4\cdot (42+1)}{10}=17,2$

ဒါပေမယ့် ဒီတစ်ခါမှာတော့ ဖော်မြူလာကနေ ဒဿမ ဂဏန်းတစ်ခု ရခဲ့ပါတယ်၊ ဒါကြောင့် decile အတိအကျကို တွက်ချက်ဖို့ အောက်ပါဖော်မြူလာကို အသုံးပြုရမှာ ဖြစ်ပါတယ်။

$D=x_i+d\cdot (x_{i+1}-x_i)$

ပထမဖော်မြူလာမှရရှိသော နံပါတ်သည် 17.2 ဖြစ်သောကြောင့် စတုတ္ထ decile သည် 109 နှင့် 112 အသီးသီး ပေးထားသော ဆယ့်ခုနစ်ခုနှင့် တစ်ဆယ့်ရှစ်ကြားဖြစ်သည်။ ထို့ကြောင့် x _i သည် 109၊ x _{i+ 1} သည် 112 ဖြစ်ပြီး d သည် ဒဿမအပိုင်းဖြစ်သည်။ ရရှိသော ကိန်းဂဏန်းများ၏ ဆိုလိုသည်မှာ 0.2 ဖြစ်သည်။

$D_4=109+0,2\cdot (112-109)=109,6$

သတ္တမမြောက် decile ကိုရှာရန် တူညီသောလုပ်ငန်းစဉ်ကို ကျွန်ုပ်တို့ပြန်လုပ်ပါသည်။ ပထမဦးစွာ decile ၏ အနေအထားကို တွက်ချက်သည် ။

$\cfrac{7\cdot (42+1)}{10}=30,1$

ဖော်မြူလာမှ ကျွန်ုပ်တို့ရရှိသော ဂဏန်း 30.1 ၊ ဆိုလိုသည်မှာ decile သည် ရာထူး 30 နှင့် 31 ကြားရှိမည်ဖြစ်ပြီး 154 နှင့် 159 ဖြစ်သည့် တန်ဖိုးများဖြစ်သည်။ ထို့ကြောင့် decile အတိအကျကို တွက်ချက်ခြင်းမှာ-

$D_7=154+0,1\cdot (159-154)=154,5$

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် နဝမမြောက် decile ကိုရရှိရန် တူညီသောနည်းလမ်းကို ထပ်မံကျင့်သုံးသည်။ ကျွန်ုပ်တို့သည် decile ၏အနေအထားကိုဆုံးဖြတ်သည်-

$\cfrac{9\cdot (42+1)}{10}=38,7$

ရရှိသောနံပါတ်သည် ဒဿမဖြစ်ပြီး ၃၈ နှင့် ၃၉ အကြားဖြစ်ပြီး၊ ၎င်း၏ရာထူးများသည် တန်ဖိုး ၁၈၉ နှင့် ၁၉၆ တို့နှင့် သက်ဆိုင်သည်။ ထို့ကြောင့် decile 9 ၏ တွက်ချက်မှုမှာ-

$D_9=189+0,7\cdot (196-189)=193,9$

Decile ဂဏန်းတွက်စက်

decis များကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်တွင် ကိန်းဂဏန်း အချက်အလက် သတ်မှတ် ချက်ကို ချိတ်ဆက်ပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာတွင် Deciles

ဒေတာများကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့်အခါ decile များကို တွက်ချက် ရန်၊ အောက်ဖော်ပြပါ ဖော်မြူလာကို အသုံးပြု၍ decile ကျရောက်သည့် ကြားကာလ သို့မဟုတ် bin ကို ဦးစွာရှာဖွေရန် လိုအပ်သည်-

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,3,4,5,6,7,8,9$

ထို့ကြောင့် decile သည် ယခင်ဖော်ပြချက်တွင်ရရှိသော ကိန်းဂဏန်းများထက် အကြွင်းမဲ့အကြိမ်ရေသည် ချက်ချင်းကြီးနေသည့်ကြားကာလတွင် ဖြစ်လိမ့်မည်။

decile ပိုင်ဆိုင်သည့် ကြားကာလကို ကျွန်ုပ်တို့ သိရှိပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် decile ၏ အတိအကျတန်ဖိုးကို ရှာဖွေရန် အောက်ပါပုံသေနည်းကို အသုံးပြုရပါမည်။

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4,5,6,7,8,9$

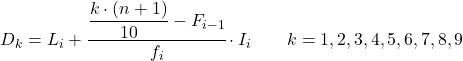
ရွှေ-

L _i သည် decile တည်ရှိသည့် ကြားကာလ၏ အနိမ့်ဆုံးကန့်သတ်ချက်ဖြစ်သည်။
n သည် စာရင်းအင်း အချက်အလက် စုစုပေါင်း အရေအတွက် ဖြစ်သည်။
F _i-1 သည် ယခင်ကြားကာလ၏ ပကတိအကြိမ်အရေအတွက်ဖြစ်သည်။
f _i သည် decile တည်ရှိသည့် ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
I _i သည် decile interval ၏ width ဖြစ်သည်။

၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို သင်မြင်နိုင်စေရန်၊ အောက်တွင် ကြားကာလအလိုက် စုဖွဲ့ထားသော အောက်ပါဒေတာများ၏ deciles 3၊ 5 နှင့် 8 တို့ကို အပြီးသတ်တွက်ချက်ထားသော လေ့ကျင့်ခန်းတစ်ခုရှိသည်။

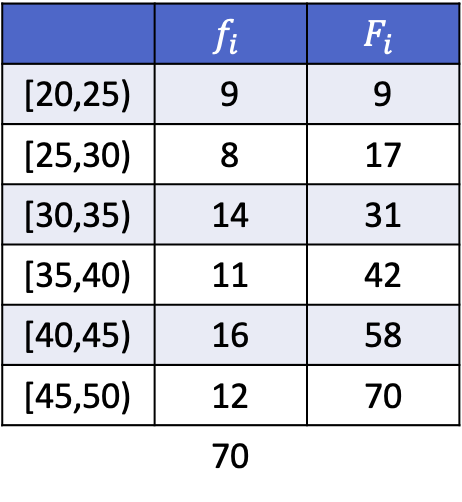
ဒေတာများကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ထားသည်။

ဒေတာကို အုပ်စုဖွဲ့ထားသောကြောင့်၊ decile တစ်ခုစီ၏တွက်ချက်မှုတွင် အဆင့်နှစ်ဆင့်ပါဝင်သည်- ပထမ၊ decile ကျရောက်သည့်ကြားကာလကိုရှာပါ၊ ထို့နောက် decile ၏တန်ဖိုးအတိအကျကို တွက်ချက်ပါ။ ထို့ကြောင့် တတိယ decile ၏ ကြားကာလကို ကျွန်ုပ်တို့ ရှာတွေ့သည် ။

$\cfrac{k\cdot (n+1)}{10}$

$\cfrac{3\cdot (70+1)}{10} =21,3 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [30,35)$

decile ကြားကာလသည် 21.3 ထက် အကြွင်းမဲ့ စုစည်းမှုအကြိမ်ရေ 21.3 ထက် ကြီးနေမည်ဖြစ်ပြီး ဤအခြေအနေတွင် ၎င်းသည် 31.35 ၏ absolute cumulative frequency ဖြစ်သည့် ကြားကာလဖြစ်သည်။ ယခု ကျွန်ုပ်တို့သည် decile ကြားကာလကို သိရှိသည့်အတွက် အောက်ပါဖော်မြူလာကို ရှာဖွေရန် အသုံးပြုပါသည်။ decile ၏အတိအကျတန်ဖိုး

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i$

$D_3=30+ \cfrac{\displaystyle\frac{3\cdot (70+1)}{10}-17}{14}\cdot 5=31,54$

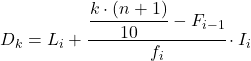
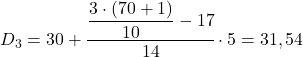
ပဉ္စမ decile ကိုရရှိရန် ယခုနည်းလမ်းကို ကျွန်ုပ်တို့ ပြန်လည်ကျင့်သုံးရမည်ဖြစ်သည်။ ကျွန်ုပ်တို့သည် ၎င်းတွင်တည်ရှိသည့် ကြားကာလကို ဦးစွာဆုံးဖြတ်သည်-

$\cfrac{5\cdot (70+1)}{10} =35,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [35,40)$

ရလဒ် 35 သည် ကြားကာလ [35,40) တွင်ရှိသည်ဟုဆိုလိုသော်လည်း ကြားကာလအသုံးအနှုန်းတွင် 35 ရှိသောကြောင့်မဟုတ်ဘဲ ၎င်း၏စုဆောင်းထားသော absolute frequency (42) သည် ချက်ချင်းအမြင့်မားဆုံးဖြစ်သောကြောင့်ဖြစ်သည်။ ကြားကာလကို ဖော်ထုတ်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် လုပ်ငန်းစဉ်၏ ဒုတိယဖော်မြူလာကို အသုံးပြုသည်-

$D_5=35+ \cfrac{\displaystyle\frac{5\cdot (70+1)}{10}-31}{11}\cdot 5=37,05$

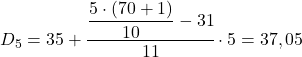
နောက်ဆုံးတွင် အဋ္ဌမမြောက် နိမိတ်ကို ရှာတွေ့သည်။ ဒါကိုလုပ်ဖို့၊ သူ့ရဲ့ကြားကာလကို ဦးစွာတွက်ချက်ပါ-

$\cfrac{8\cdot (70+1)}{10} =56,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [40,45)$

56.8 အထက် ချက်ချင်း စုစည်းနိုင်သော ပကတိကြိမ်နှုန်းသည် 58 ဖြစ်ပြီး၊ ထို့ကြောင့် အဋ္ဌမမြောက် ကိန်းဂဏန်းသည် [40.45) ဖြစ်သည်။ ထို့ကြောင့် decile ၏ တိကျသောတန်ဖိုးကို ဆုံးဖြတ်ရန် လုံလောက်ပါသည်။

$D_8=40+ \cfrac{\displaystyle\frac{8\cdot (70+1)}{10}-42}{16}\cdot 5=44,63$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။