Quintiles (စာရင်းအင်းများ)

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် quintiles သည် မည်ကဲ့သို့ တွက်ချက်သည်ကို ရှင်းပြပါသည်။ quintiles များကို တွက်ချက်ခြင်း၏ ဖြေရှင်းနိုင်သော ဥပမာများစွာကို သင်တွေ့ရှိနိုင်ပြီး ထို့အပြင်၊ မည်သည့်ကိန်းဂဏန်းနမူနာ၏ quintiles များကို အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် တွက်ချက်နိုင်မည်ဖြစ်သည်။

Quintiles တွေက ဘာတွေလဲ။

စာရင်းဇယားများတွင်၊ Quintiles သည် ဒေတာကို အပိုင်းငါးပိုင်းခွဲ၍ ညီမျှသောတန်ဖိုးလေးခုဖြစ်သည်။ ထို့ကြောင့်၊ ပထမ၊ ဒုတိယ၊ တတိယနှင့် စတုတ္ထ quintiles များသည် နမူနာဒေတာ၏ 20%, 40%, 60% နှင့် 80% တို့ကို ကိုယ်စားပြုပါသည်။

ဆိုလိုသည်မှာ၊ ဥပမာအားဖြင့်၊ တတိယ quintile ၏တန်ဖိုးသည် စုဆောင်းထားသောဒေတာအားလုံး၏ 60% ထက် မြင့်မားသော်လည်း ကျန်ဒေတာများထက် နိမ့်ပါသည်။

quintiles အတွက် သင်္ကေတမှာ quintile အညွှန်းနှင့်အတူ စာလုံးကြီး K ဖြစ်ပြီး ပထမ Quintile မှာ K ₁ ဖြစ်ပြီး ဒုတိယ Quintile မှာ K ₂ ဖြစ်ပြီး တတိယ Quintile မှာ K ₃ ဖြစ်ပြီး စတုတ္ထ Quintile မှာ K ₄ ဖြစ်သည်။ ၎င်းကို အက္ခရာ Q ဖြင့်လည်း ကိုယ်စားပြုနိုင်သော်လည်း (၎င်းသည် quartiles များနှင့် ရှုပ်ထွေးမှုကို ဖြစ်စေသောကြောင့် မထောက်ခံပါ)။

👉 မည်သည့်ဒေတာအစုံအတွက်မဆို quintiles တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

Quintiles များသည် quartiles၊ deciles နှင့် percentiles များနှင့်အတူ ဗဟိုမဟုတ်သော အနေအထားကို တိုင်းတာခြင်းဖြစ်သည်။ သင်ပိုမိုစိတ်ဝင်စားပါက၊ ဤပမာဏအမျိုးအစားတစ်ခုစီသည် ကျွန်ုပ်တို့၏ဝဘ်ဆိုက်တွင် ဘာကိုဆိုလိုကြောင်း စစ်ဆေးနိုင်ပါသည်။

Quintile သည် အခြားအဓိပ္ပါယ်ရှိနိုင်သည်ကို သတိပြုသင့်သည်။ ဘောဂဗေဒတွင်၊ quintiles သည် ဝင်ငွေဖြင့်သတ်မှတ်ထားသော လူဦးရေ၏ ရာခိုင်နှုန်းကို ကိုယ်စားပြုသည်၊ သို့မဟုတ် တစ်နည်းအားဖြင့် ၎င်းတို့သည် လူဦးရေကို ဝင်ငွေအဆင့်ဖြင့် အဆင့်သတ်မှတ်သည်။ ဥပမာအားဖြင့်၊ ပထမ quintile သည် လူဦးရေ၏ အဆင်းရဲဆုံး 20% နှင့် သက်ဆိုင်ပြီး၊ ဒုတိယ quintile သည် ၀င်ငွေအနည်းဆုံး လူဦးရေ၏ 40% နှင့် ဆက်စပ်ပါသည်။

Quintiles တွက်နည်း

နမူနာ သို့မဟုတ် ကိန်းဂဏန်းလူဦးရေ၏ quintiles ၏ အနေအထားကို တွက်ချက် ရန်၊ သင်သည် အချက်အလက်စုစုပေါင်း၏ ပေါင်းလဒ်နှင့် quintiles အရေအတွက်ကို မြှောက်ပြီး ရလဒ်ကို ငါးဖြင့် ပိုင်းခြားရပါမည်။

ထို့ကြောင့်၊ quintiles အတွက်ဖော်မြူလာ မှာ-

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာ၏ရလဒ်သည် ၎င်း၏တန်ဖိုးမဟုတ်ဘဲ quintile ၏အနေအထားကို ကျွန်ုပ်တို့အားပြောပြသည်။ ထို့ကြောင့် quintile သည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော အချက်အလက်ဖြစ်လိမ့်မည်။

သို့သော်၊ တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်၊ ထို့ကြောင့် ရလဒ်သည် ဒဿမကိန်းဖြစ်ခြင်း ရှိ၊ မရှိအပေါ် မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ quintile သည် အထက်ဖော်ပြပါပုံသေနည်းမှ ပေးထားသည့် အနေအထားတွင်ရှိသော ဒေတာဖြစ်သည်။
ဖော်မြူလာရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း ဖြစ်ပါက၊ quintile တန်ဖိုးကို အောက်ပါစကားရပ်ဖြင့် တွက်ချက်သည်-

$K=x_i+d\cdot (x_{i+1}-x_i)$

x _i နှင့် x _i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။

ဒေတာအစုတစ်ခု၏ quintiles ကိုဆုံးဖြတ်ရန် အဆင့်များစွာကို သင်မြင်သောအခါ သင်ကြောက်ရွံ့နေပါက၊ စိတ်မပူပါနှင့်၊ ၎င်းသည် အမှန်တကယ်ရိုးရှင်းပါသည်။ အောက်ပါဥပမာနှစ်ခုကိုဖတ်ကြည့်လျှင် သင်ပိုမိုနားလည်လာမည်မှာ သေချာပါသည်။

မှတ်ချက် – ကိန်းဂဏန်းအသိုက်အဝန်းသည် quintiles များကို မည်ကဲ့သို့ တွက်ချက်သည်ကို လုံး၀ သဘောမတူသေးသောကြောင့် ၎င်းကို အနည်းငယ်ကွဲပြားစွာ ရှင်းပြထားသည့် စာအုပ်တစ်အုပ်ကို သင်ရှာတွေ့နိုင်ပါသည်။

quintiles တွက်ချက်ခြင်း ဥပမာများ

အောက်တွင် ကျွန်ုပ်တို့သည် သင့်အား ဒေတာစီးရီးတစ်ခုမှ quintiles ရယူနည်းအတွက် တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းနှစ်ခုကို ချန်ထားပေးပါသည်။ ဒါကြောင့် ဖြစ်နိုင်ခြေရှိတဲ့ ကိစ္စနှစ်ခုကို သင်မြင်နိုင်တယ်၊ ပထမလေ့ကျင့်ခန်းမှာ ရလဒ်တွေက ဒဿမမဖြစ်ပြီး ဒုတိယလေ့ကျင့်ခန်းမှာ အဲဒါတွေက ရလဒ်တွေပါ။

ဥပမာ ၁

အောက်ပါဒေတာစီးရီးများ၏ quintiles ကိုတွက်ချက်ပါ-

အထက်ဖော်ပြပါ ရှင်းလင်းချက်တွင် သင်တွေ့ခဲ့သည့်အတိုင်း၊ quintiles များ၏ အနေအထားကို ရှာဖွေရန် ဖော်မြူလာမှာ-

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ကန့်သတ်ချက် n သည် 49 ဖြစ်ပြီး ဒေတာစုစုပေါင်းအရေအတွက်ကို ရည်ညွှန်းသည်၊ ထို့ကြောင့် ပထမ quintile ၏အနေအထားကိုရှာဖွေရန် n ကို 49 နှင့် k ကို 1 ဖြင့် အစားထိုးရန်လိုအပ်သည်-

$\cfrac{1\cdot (49+1)}{5}=10 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_1=205$

ဖော်မြူလာမှ ကျွန်ုပ်တို့သည် နံပါတ် 10 ကိုရရှိခဲ့သည်၊ ဆိုလိုသည်မှာ quintile သည် ဒေတာ 205 နှင့် ကိုက်ညီသော မှာယူထားသောစာရင်း၏ ဒသမ အနေအထားတွင် ရှိနေပါသည်။

ဒုတိယ quintile ကို တွက်ချက်ရန် တူညီသော ဖော်မြူလာကို အသုံးပြုရမည်ဖြစ်ပြီး k ကို 2 ဖြင့် အစားထိုးခြင်း-

$\cfrac{2\cdot (49+1)}{5}=20 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_2=236$

ထို့ကြောင့် ဒုတိယ quintile သည် မှာယူထားသော စာရင်း၏ နံပါတ် 20 တွင် ဖြစ်သည်၊ ဆိုလိုသည်မှာ တန်ဖိုး 236 ကို ဆိုလိုပါသည်။

တဖန်၊ ကျွန်ုပ်တို့သည် quintile 3 ကိုဆုံးဖြတ်ရန် လုပ်ငန်းစဉ်ကို ထပ်ခါတလဲလဲ လုပ်ဆောင်သော်လည်း၊ ယုတ္တိနည်းအရ၊ ယခု ကျွန်ုပ်တို့သည် k ကို 3 ဖြင့် အစားထိုးသည်-

$\cfrac{3\cdot (49+1)}{5}=30 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_3=266$

ထို့ကြောင့် တတိယ quintile သည် position 30 တွင်ရှိသော data ဖြစ်ပြီး 266 နှင့် ကိုက်ညီပါသည်။

နောက်ဆုံးတွင်၊ စတုတ္ထမြောက် Quintile ကိုတွက်ချက်ရန် ဖော်မြူလာကို ထပ်မံအသုံးပြုသည်-

$\cfrac{4\cdot (49+1)}{5}=40 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_4=286$

စတုတ္ထ quintile သည် အနေအထား 40 တွင် ရှိသည်၊ ထို့ကြောင့် စတုတ္ထ quintile သည် 286 ဖြစ်သည်။

ဥပမာ ၂

အောက်ပါဇယားတွင် စုဆောင်းထားသော ကိန်းဂဏန်းအချက်အလက်များ၏ quintiles လေးခုကို တွက်ချက်ပါ။

ယခင်ဥပမာတွင်ကဲ့သို့ပင်၊ quintiles ၏ရာထူးများကိုရယူရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည်။

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ဤကိစ္စတွင်၊ နမူနာအရွယ်အစားသည် 42 ရှုမြင်ချက်များဖြစ်သည်၊ ထို့ကြောင့် ပထမ quintile ၏အနေအထားကိုရှာဖွေရန် parameter n ကို 42 နှင့် k ကို 1 ဖြင့်အစားထိုးရန်လိုအပ်သည်-

$\cfrac{1\cdot (42+1)}{5}=8,6$

သို့သော် ပထမဥပမာနှင့်မတူဘဲ၊ ဤအကြိမ်တွင် ဖော်မြူလာသည် ကျွန်ုပ်တို့အား ဒဿမဂဏန်းတစ်ခုပေးသည်၊ ထို့ကြောင့် အတိအကျ quintile ကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရန်လိုအပ်သည်-

$K=x_i+d\cdot (x_{i+1}-x_i)$

ပထမဖော်မြူလာမှရရှိသောနံပါတ်သည် 8.6 ဖြစ်ပြီး၊ ထို့ကြောင့် ပထမ quintile သည် 78 နှင့် 79 အသီးသီးဖြစ်သည့် အဋ္ဌမနှင့် နဝမဒေတာကြားတွင်ဖြစ်သည်။ ထို့ကြောင့် x _i သည် 78 ၊ x _{i + 1} သည် 79 ဖြစ်ပြီး d သည် ရရှိသော ဂဏန်းများ၏ ဒဿမ အပိုင်းဖြစ်သည် ၊ ဆိုလိုသည်မှာ 0.6 ဖြစ်သည်။

$K_1=78+0,6\cdot (79-78)=78,6$

ယခု ကျွန်ုပ်တို့သည် ဒုတိယ quintile ကိုရှာဖွေရန် တူညီသောလုပ်ငန်းစဉ်ကို ထပ်မံပြုလုပ်ပါသည်။ ကျွန်ုပ်တို့သည် ၎င်း၏ရာထူးကို ဦးစွာတွက်ချက်သည်-

$\cfrac{2\cdot (42+1)}{5}=17,2$

သို့သော် ဖော်မြူလာမှ ကျွန်ုပ်တို့သည် 17 နှင့် 18 ကြားတွင် ဒဿမ ဂဏန်းကို ရယူထားသောကြောင့် ဒုတိယ quintile သည် 17th နှင့် 18th ရာထူးများကြားတွင် ရှိနေမည်ဖြစ်ပြီး၊ တန်ဖိုးများသည် မှာယူထားသောစာရင်း၏ 109 နှင့် 112 တို့နှင့် အသီးသီး သက်ဆိုင်ပါသည်။ ထို့ကြောင့်၊ တိကျသော quintile တန်ဖိုးကို ဆုံးဖြတ်ရန် လုပ်ငန်းစဉ်တွင် ဒုတိယဖော်မြူလာကို အသုံးပြုပါသည်။

$K_2=109+0,2\cdot (112-109)=109,6$

တတိယအကြိမ် quintile ရရှိရန် နည်းလမ်းကို ထပ်ခါတလဲလဲ၊ ၎င်း၏ အနေအထားကို ဦးစွာ ဆုံးဖြတ်ပါသည်။

$\cfrac{3\cdot (42+1)}{5}=25,8$

တွက်ချက်ထားသော နံပါတ် 25.8 သည် quintile တန်ဖိုးသည် နှစ်ဆယ့်ငါးခုနှင့် နှစ်ဆယ့်ခြောက်ခုမြောက် အနေအထားကြားတွင် ရှိနေမည်ကို ဆိုလိုပြီး တန်ဖိုးများမှာ 134 နှင့် 141 ဖြစ်သည်။ အတိအကျ quintile တန်ဖိုးကို တွက်ချက်ခြင်းမှာ-

$K_3=134+0,8\cdot (141-134)=139,6$

နောက်ဆုံးတွင်၊ quintile 4 ကို တွက်ချက်ရန် နောက်ဆုံးအကြိမ် တူညီသောလုပ်ငန်းစဉ်ကို ထပ်လုပ်ပါသည်။ ၎င်း၏ အနေအထားကို ကျွန်ုပ်တို့ ပထမဆုံးရှာသည်-

$\cfrac{4\cdot (42+1)}{5}=34,4$

ထို့ကြောင့် စတုတ္ထ quintile ၏ အတိအကျတန်ဖိုးသည် 34 နှင့် 35 အကြားရှိမည်ဖြစ်ပြီး၊ တည်နေရာများသည် data 172 နှင့် 179 နှင့် သက်ဆိုင်ပါသည်။ စတုတ္ထ quintile ၏တွက်ချက်မှုသည်-

$K_4=172+0,4\cdot (179-172)=174,8$

Quintile ဂဏန်းပေါင်းစက်

quintiles များကိုတွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်များကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာတွင် Quintiles

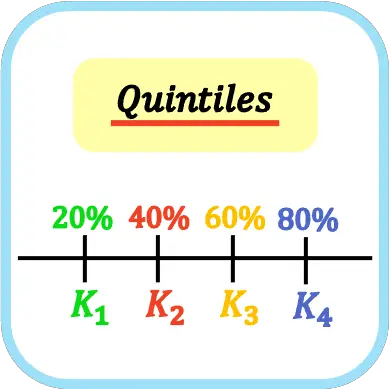
ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့လိုက်သောအခါ quintiles များကို တွက်ချက်ရန်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ ၎င်း၏ကြားကာလ သို့မဟုတ် အတန်းကို ဦးစွာရှာရပါမည်။

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ထို့ကြောင့် quintile သည် ယခင်ဖော်ပြချက်ဖြင့်ရရှိသော အကြိမ်အရေအတွက်ထက် သာလွန်သောကြိမ်နှုန်းသည် ချက်ချင်းကြီးနေသည့်ကြားကာလတွင် ဖြစ်လိမ့်မည်။

quintile ပိုင်ဆိုင်သည့် ကြားကာလကို ကျွန်ုပ်တို့သိသည်နှင့်၊ ကျွန်ုပ်တို့သည် quintile ၏အတိအကျတန်ဖိုးကိုရှာဖွေရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည်။

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4$

ရွှေ-

L _i သည် quintile တည်ရှိသည့်ကြားကာလ၏ အနိမ့်ဆုံးကန့်သတ်ချက်ဖြစ်သည်။
n သည် လေ့လာတွေ့ရှိချက် စုစုပေါင်း အရေအတွက်ဖြစ်သည်။
F _i-1 သည် ယခင်ကြားကာလ၏ ပကတိအကြိမ်အရေအတွက်ဖြစ်သည်။
f _i သည် quintile တည်ရှိသည့် ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
_{ငါသည်} quintile ကြားကာလ၏အကျယ်ဖြစ်သည်။

ဤအရာသည် မည်သို့ပြီးမြောက်သည်ကို သင်မြင်နိုင်သည်၊ ဤသည်မှာ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော အောက်ပါဒေတာစီးရီးများ၏ quintiles များကို တွက်ချက်ခြင်း၏ ဖြေရှင်းနိုင်သော ဥပမာတစ်ခုဖြစ်သည်။

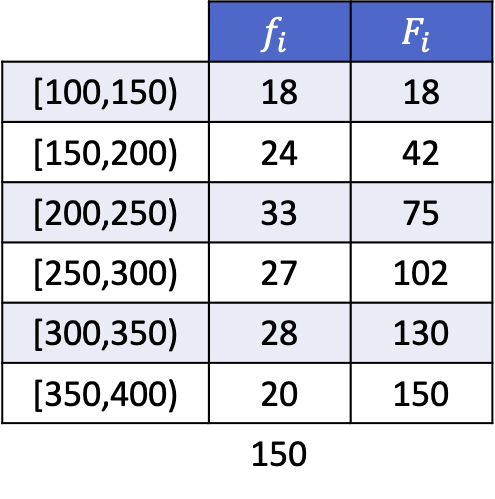
ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာအစု

ဒေတာကို အုပ်စုဖွဲ့ထားသောကြောင့်၊ quintiles များကို တွက်ချက်ရန် အောက်ပါနည်းလမ်းကို အသုံးပြုရပါမည်- quintile ကျရောက်သည့် အကွာအဝေးကို ဦးစွာဆုံးဖြတ်ပါ၊ ထို့နောက် quintile ၏ အတိအကျတန်ဖိုးကို ရှာပါ။

ထို့ကြောင့်၊ ပထမ quintile တည်ရှိသည့်ကြားကာလကိုရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာကို အသုံးပြုသည်-

$\cfrac{k\cdot (n+1)}{5}$

$\cfrac{1\cdot (150+1)}{5} =30,2 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [150,200)$

ပထမအကြိမ် quintile သည် 30.2 ထက် ချက်ချင်းပို၍ တိုးပွားလာသော အကြွင်းမဲ့ကြိမ်နှုန်းကြားကာလတွင် ဖြစ်လိမ့်မည်၊ ဤအခြေအနေတွင်၊ ၎င်းသည် တိုးပွားနေသော ပကတိအကြိမ်ရေ 42 ဖြစ်သည့် ကြားကာလ (150,200) ဖြစ်သည်။ ထို့နောက် quintile ကြားကာလကို ကျွန်ုပ်တို့သိသည်နှင့်၊ ကျွန်ုပ်တို့သည် ဒုတိယပုံသေနည်းကို အသုံးပြုပါသည်။ ၎င်း၏တန်ဖိုးအတိအကျကို ဆုံးဖြတ်ရန် လုပ်ငန်းစဉ်

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i$

$K_1=150+\cfrac{\displaystyle\frac{1\cdot (150+1)}{5}-18}{24}\cdot 50=175,42$

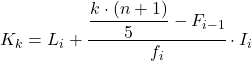
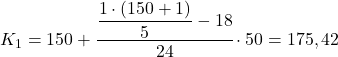
ယခု ကျွန်ုပ်တို့သည် ဒုတိယ quintile ကိုရရှိရန် တူညီသောလုပ်ငန်းစဉ်ကို ထပ်မံပြုလုပ်ပြီး ၎င်းတွင်ရှိသော ကြားကာလကို ဦးစွာတွက်ချက်ခြင်းဖြစ်သည်-

$\cfrac{2\cdot (150+1)}{5} =60,4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [200,250)$

60.4 အထက် ချက်ချင်း စုစည်းနိုင်သော အကြွင်းမဲ့ ကြိမ်နှုန်းသည် 75 ဖြစ်ပြီး၊ ထို့ကြောင့် ဒုတိယ quintile အပိုင်းသည် [200 250) ဖြစ်သည်။ ထို့ကြောင့်၊ အတိအကျ quintile တန်ဖိုးကိုတွက်ချက်ရန် သက်ဆိုင်ရာတန်ဖိုးများကို ဒုတိယဖော်မြူလာတွင် အစားထိုးသည်-

$K_2=200+\cfrac{\displaystyle\frac{2\cdot (150+1)}{5}-42}{33}\cdot 50=227,88$

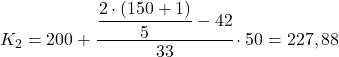
quintile 3 ကိုရရှိရန်ကျွန်ုပ်တို့သည်တူညီသောလုပ်ငန်းစဉ်ကိုတတိယအကြိမ်လုပ်ဆောင်သည်။

$\cfrac{3\cdot (150+1)}{5} =90,6 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [250,300)$

၎င်း၏ စုစည်းမှု ပကတိအကြိမ်ရေ (102) သည် 90.6 အထက် ချက်ချင်းဖြစ်သောကြောင့် quintile သည် ကြားကာလ [250,300) ဖြစ်သည်။ ထို့ကြောင့် တတိယ Quintile ၏ အတိအကျတန်ဖိုးကို တွက်ချက်ရာတွင် အောက်ပါအတိုင်းဖြစ်သည်။

$K_3=250+\cfrac{\displaystyle\frac{3\cdot (150+1)}{5}-75}{27}\cdot 50=278,89$

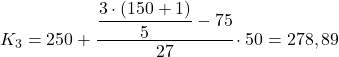
နောက်ဆုံးတွင်၊ စတုတ္ထ quintile ကိုတွေ့လိမ့်မည်။ အမြဲလိုလို၊ ကျွန်ုပ်တို့သည် ၎င်း၏ကြားကာလကို ဦးစွာရှာဖွေသည်-

$\cfrac{4\cdot (150+1)}{5} =120,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [300,350)$

အကြွင်းမဲ့ အကြိမ်ရေ 120.8 ထက် ချက်ချင်းကြီးသော ကြားကာလသည် [300.350) ဖြစ်ပြီး တန်ဖိုးသည် 130 ဖြစ်သည်။ ထို့ကြောင့် စတုတ္ထ quintile ၏ အတိအကျတန်ဖိုးသည်-

$K_4=300+\cfrac{\displaystyle\frac{4\cdot (150+1)}{5}-102}{28}\cdot 50=333,57$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

Quintiles တွေက ဘာတွေလဲ။

Quintiles တွက်နည်း

quintiles တွက်ချက်ခြင်း ဥပမာများ

ဥပမာ ၁

ဥပမာ ၂

Quintile ဂဏန်းပေါင်းစက်

အုပ်စုဖွဲ့ဒေတာတွင် Quintiles

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။