Ti-84 ဂဏန်းတွက်စက်ပေါ်တွင် quadratic regression လုပ်ဆောင်နည်း
ကိန်းရှင်နှစ်ခုသည် linear ဆက်ဆံရေးတစ်ခုရှိသောအခါ၊ ၎င်းတို့၏ဆက်နွယ်မှုကို တွက်ချက်ရန် ရိုးရှင်းသော linear regression ကို အသုံးပြုနိုင်သည် ။

သို့သော်၊ ကိန်းရှင်နှစ်ခုသည် လေးထောင့်ပုံစံ ဆက်နွယ်မှုရှိပါက၊ ၎င်းတို့၏ ဆက်နွယ်မှုကို တွက်ချက်ရန် လေးထောင့်ဆုတ်ယုတ်မှုကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဤသင်ခန်းစာသည် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။
ဥပမာ- TI-84 ဂဏန်းတွက်စက်ပေါ်ရှိ လေးပုံတပုံ ဆုတ်ယုတ်မှု
အလုပ်လုပ်တဲ့နာရီအရေအတွက်နဲ့ ပျော်ရွှင်မှုကြားက ဆက်နွယ်မှုကို နားလည်ချင်တယ်ဆိုပါစို့။ ကျွန်ုပ်တို့တွင် တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်နှင့် ပတ်သက်သည့် အောက်ပါဒေတာနှင့် မတူညီသောလူ 11 ဦးအတွက် ပျော်ရွှင်မှုအဆင့် (0 မှ 100 အထိ) အစီရင်ခံတင်ပြပါသည်-

TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို လိုက်နာပါ။
အဆင့် 1- ဒေတာကို မြင်ယောင်ကြည့်ပါ။
quadratic regression ကိုအသုံးမပြုမီ၊ ရှင်းပြထားသော variable (နာရီ) နှင့် response variable (happiness) သည် quadratic အမှန်ဖြစ်ကြောင်း သေချာစေရမည်။
ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် explanatory variable နှင့် response variable အတွက် ဒေတာတန်ဖိုးများကို ထည့်သွင်းပါမည်။ Stat ကိုနှိပ်ပြီး EDIT ကို နှိပ်ပါ။ ကော်လံ L1 တွင် ရှင်းလင်းချက်ကွဲလွဲချက် (အလုပ်ချိန်) အတွက် အောက်ပါတန်ဖိုးများနှင့် ကော်လံ L2 ရှိ တုံ့ပြန်မှုကိန်းရှင် (ပျော်ရွှင်မှု) အတွက် တန်ဖိုးများကို ထည့်သွင်းပါ-
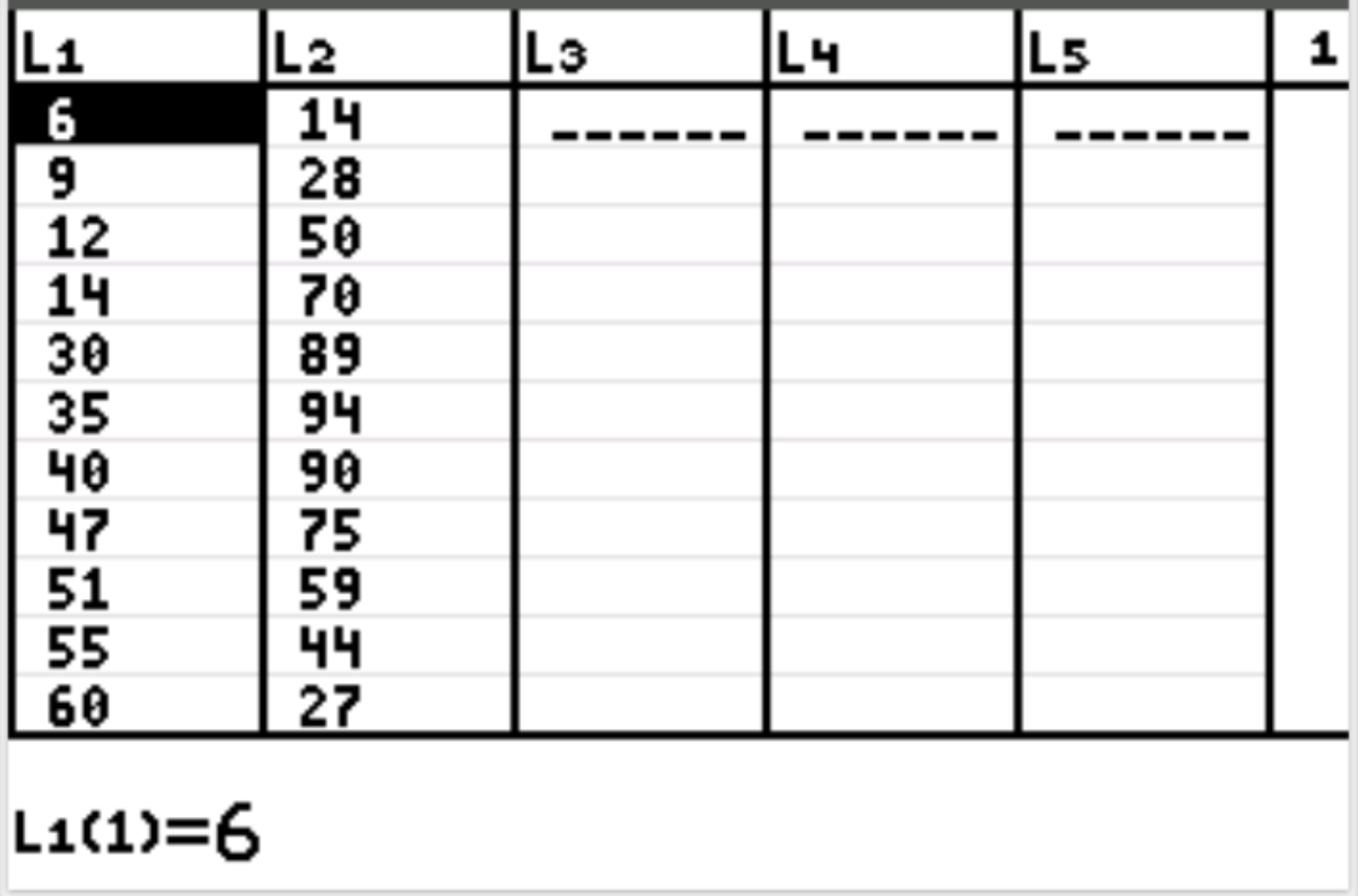
ထို့နောက် 2nd ကိုနှိပ်ပြီး statplot menu ကိုဝင်ရောက်ရန် y= ကို နှိပ်ပါ။ Plot1 ကို အသားပေး၍ Enter နှိပ်ပါ။ ပုံဆွဲခြင်းကို ဖွင့်ထားပြီး L1 နှင့် L2 ကို Xlist နှင့် Ylist အသီးသီးအတွက် ရွေးချယ်ထားကြောင်း သေချာပါစေ။
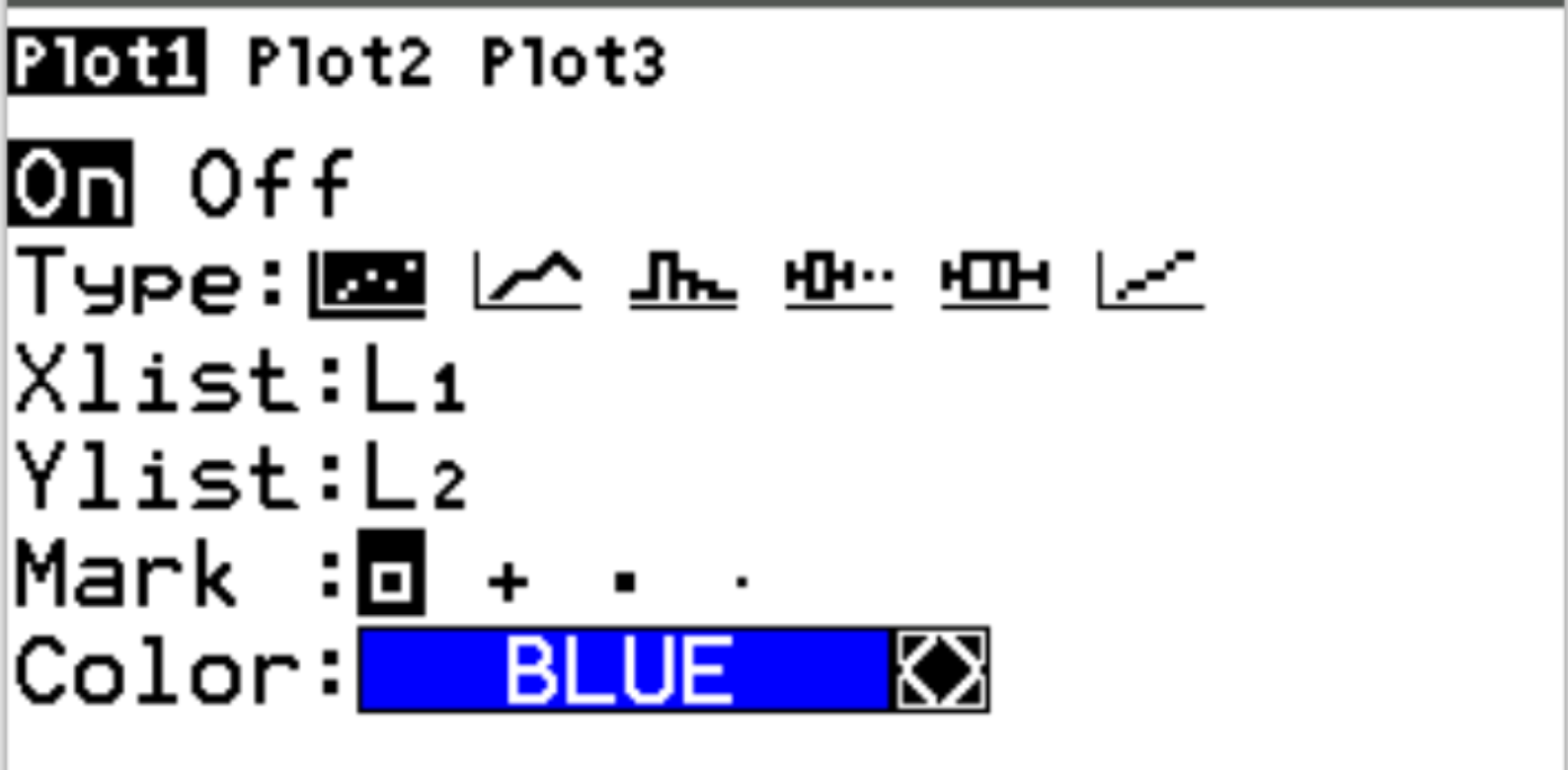
ထို့နောက် Zoom ကိုနှိပ်ပြီး 9:ZoomStat ကိုနှိပ်ပါ။ ၎င်းသည် အောက်ပါ point cloud ကို အလိုအလျောက် ထုတ်ပေးလိမ့်မည်-

အလုပ်ချိန် အရေအတွက် သုညမှ တစ်နေရာသို့ တိုးလာသည်နှင့်အမျှ ပျော်ရွှင်မှု တိုးလာတတ်သည်ကို ကျွန်ုပ်တို့ တွေ့မြင်နိုင်သော်လည်း အလုပ်ချိန်များ ပိုမိုများပြားလာသည်နှင့်အမျှ လျော့နည်းလာပါသည်။
scatterplot တွင် ပြောင်းပြန်ထားသော ဤ “ U” ပုံသဏ္ဍာန်သည် အလုပ်ချိန်နှင့် ပျော်ရွှင်မှုကြားတွင် လေးထောင့်ပုံသဏ္ဍာန် ဆက်စပ်မှုကို ညွှန်ပြသည်၊ ဆိုလိုသည်မှာ ဤဆက်ဆံရေးကို တွက်ဆရန် quadratic regression ကို သုံးသင့်သည်။
အဆင့် 2- လေးထောင့်ပုံစံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါ။
ထို့နောက်၊ ကျွန်ုပ်တို့သည် လေးထောင့်ပုံသဏ္ဍန်ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါမည်။ Stat ကိုနှိပ်ပြီး CALC သို့ ရွှေ့ပါ။ ထို့နောက် 5:QuadReg သို့ ရွှေ့ပြီး Enter နှိပ်ပါ။
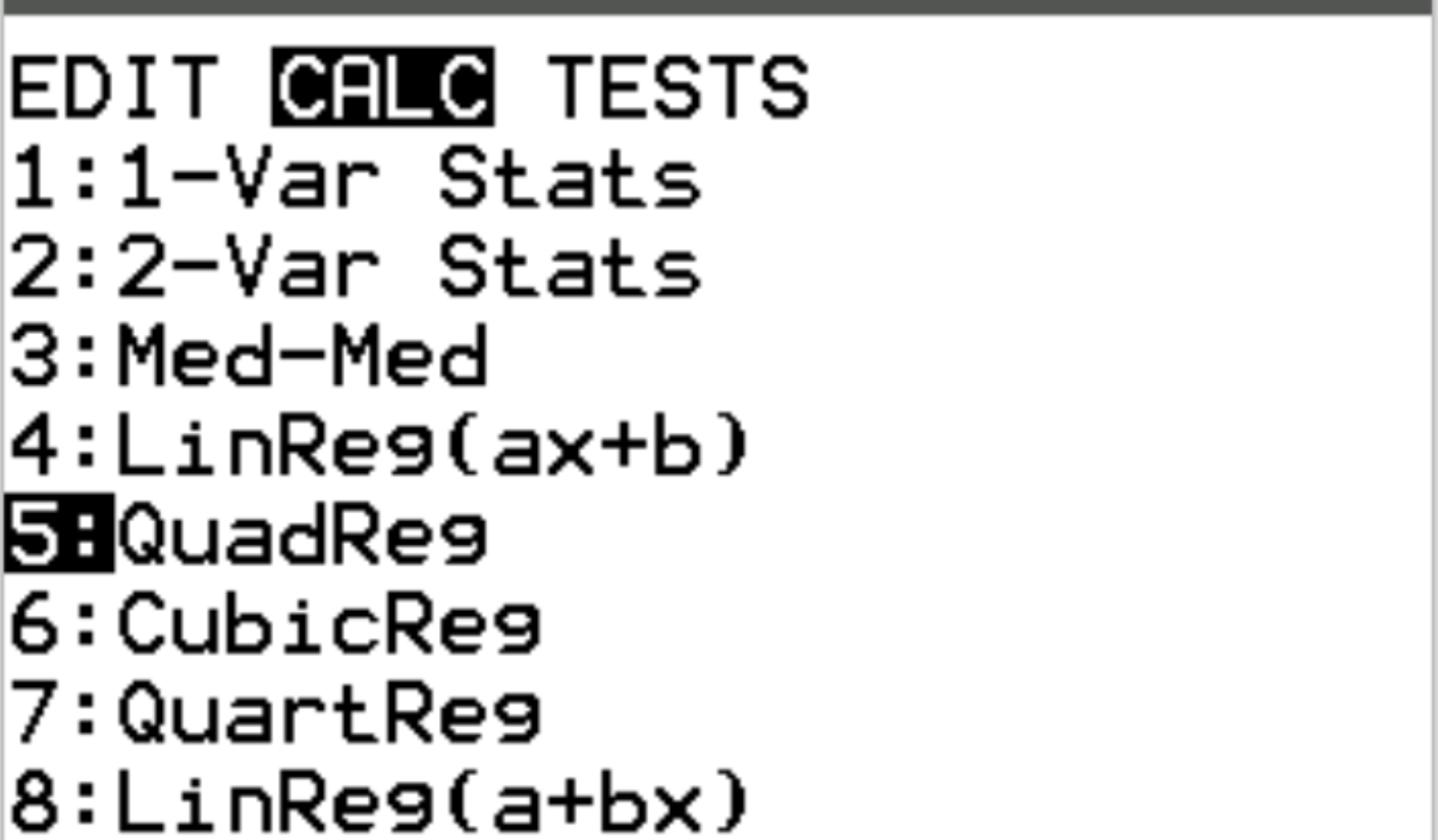
Xlist နှင့် Ylist အတွက်၊ ဤအရာများသည် ကျွန်ုပ်တို့၏ဒေတာထည့်သွင်းရန်အသုံးပြုသည့်ကော်လံများဖြစ်သောကြောင့် L1 နှင့် L2 ကို ရွေးချယ်ထားကြောင်း သေချာပါစေ။ FreqList ကို ကွက်လပ်ထားလိုက်ပါ။ တွက်ချက်ရန် အောက်သို့ဆင်းပြီး Enter နှိပ်ပါ။
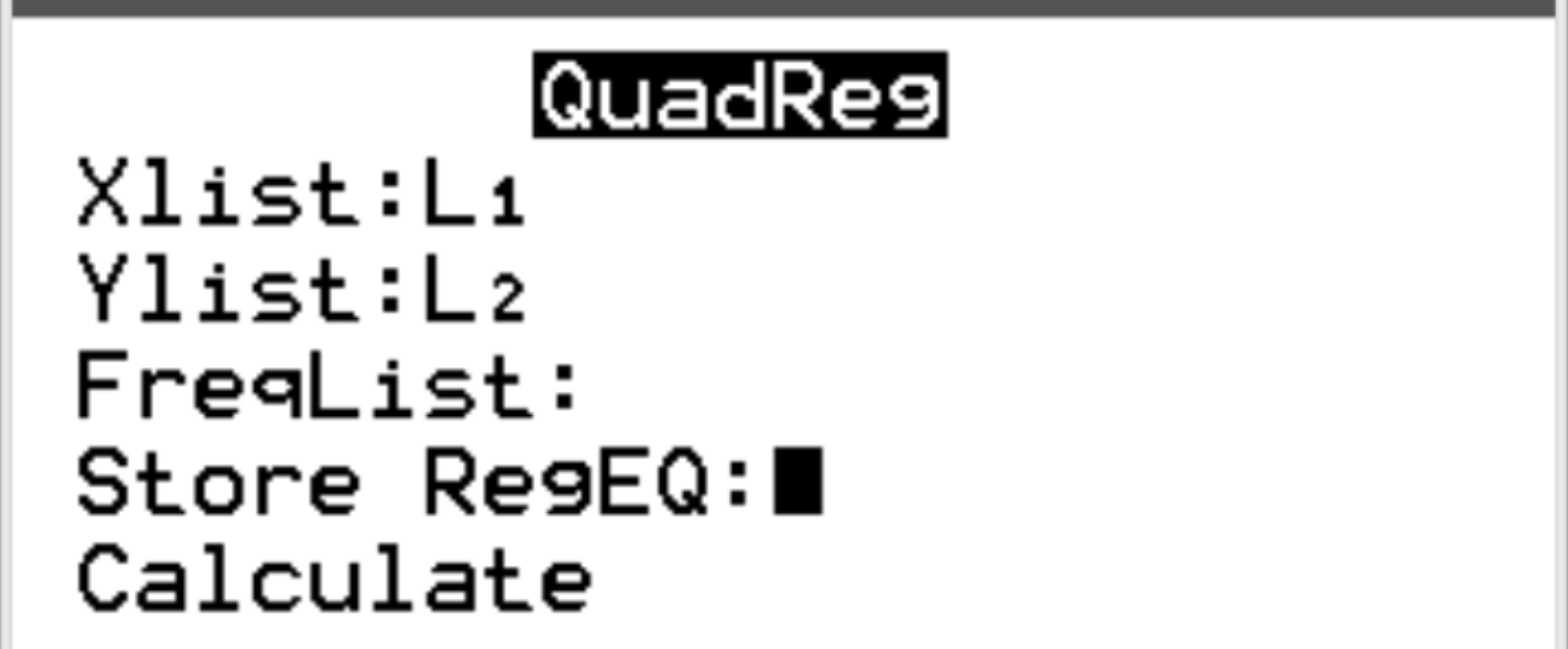
အောက်ပါ output သည် အလိုအလျောက် ပေါ်လာလိမ့်မည်-
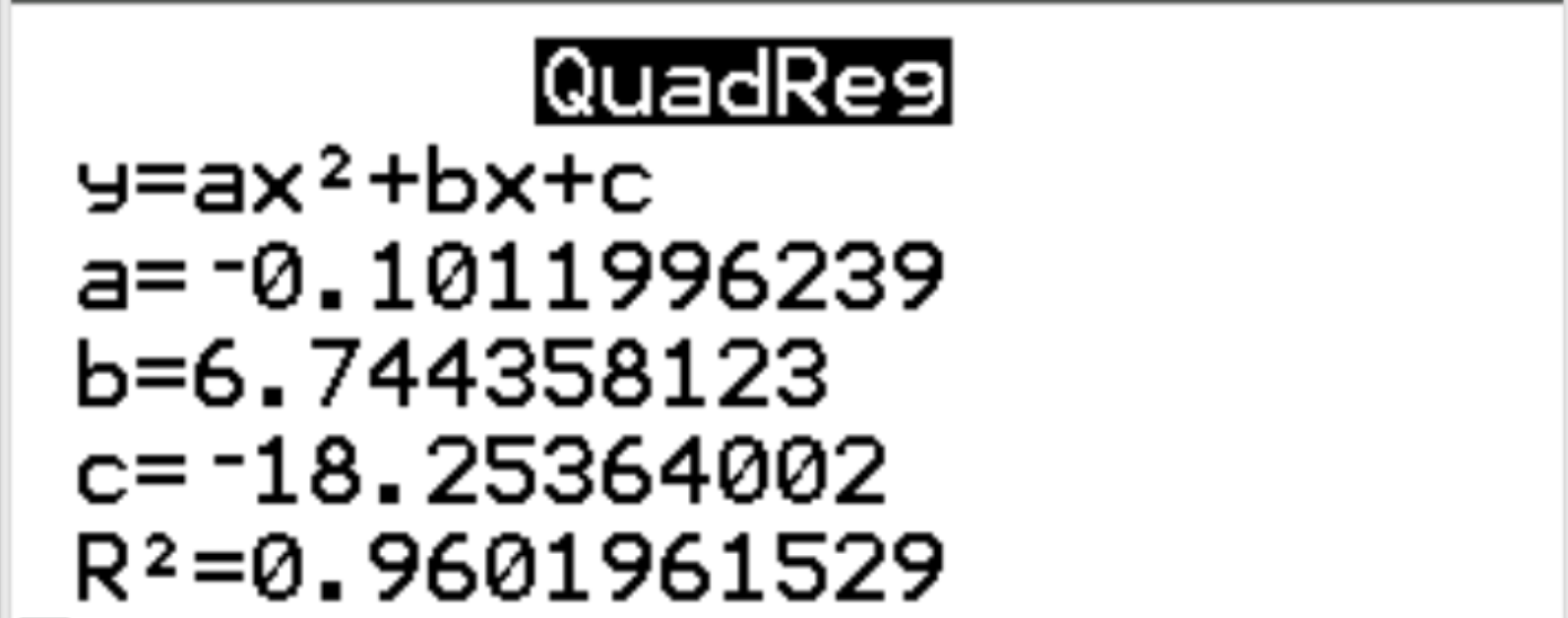
အဆင့် 3- ရလဒ်ကို ဘာသာပြန်ပါ။
ရလဒ်များမှ၊ ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-
ပျော်ရွှင်မှု = -0.1012 (နာရီ) 2 + 6.7444 (နာရီ) – 18.2536
တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်ဖြင့် လူတစ်ဦးချင်းစီ၏ ခန့်မှန်းထားသော ပျော်ရွှင်မှုကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။
ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် နာရီ 60 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 22.09 ရှိလိမ့်မည် ။
ပျော်ရွှင်မှု = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
အပြန်အလှန်အားဖြင့် တစ်ပတ်လျှင် နာရီ 30 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 92.99 ရှိသင့်သည် ။
ပျော်ရွှင်မှု = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99
ဆုတ်ယုတ်မှုပုံစံအတွက် r နှစ်ထပ်ကိန်းသည် r 2 = 0.9602 ဟုလည်း မြင်နိုင်သည်။ ဤသည်မှာ ရှင်းလင်းချက် ကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ ပျော်ရွှင်မှု၏ 96.02% ကွဲပြားမှုကို နာရီ နှင့် အကြိမ် 2 ဖြင့် ရှင်းပြနိုင်သည်။