Ti-84 ဂဏန်းတွက်စက်ပေါ်တွင် chi-square အံဝင်ခွင်ကျစမ်းသပ်မှု
Chi-square goodness-of-fit test ကို categorical variable သည် hypothetical distribution ကို လိုက်နာခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုပါသည်။
ဤသင်ခန်းစာသည် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် chi-square အံဝင်ခွင်ကျစမ်းသပ်နည်းကို ရှင်းပြထားသည်။
ဥပမာ- TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် Chi-square အံဝင်ခွင်ကျစမ်းသပ်မှု
စတိုးဆိုင်ပိုင်ရှင်တစ်ဦးက သူ့ဆိုင်ကို အပတ်စဉ် ဖောက်သည်အရေအတွက် တူညီစွာလာရောက်သည်ဟု ဆိုသည်။ ဤယူဆချက်ကို စမ်းသပ်ရန်အတွက် လွတ်လပ်သောသုတေသီတစ်ဦးသည် သတ်မှတ်ရက်သတ္တပတ်တစ်ခုအတွင်း စတိုးဆိုင်သို့လာရောက်သော ဖောက်သည်အရေအတွက်ကို မှတ်တမ်းတင်ပြီး အောက်ပါတို့ကို တွေ့ရှိသည်-
- တနင်္လာနေ့- ဖောက်သည် ၅၀
- အင်္ဂါနေ့- ဖောက်သည် ၆၀
- ဗုဒ္ဓဟူးနေ့- ဖောက်သည် ၄၀
- ကြာသပတေးနေ့: ဖောက်သည် 47
- သောကြာနေ့: ဖောက်သည် 53 ဦး
ဒေတာသည် စတိုးပိုင်ရှင်၏ တောင်းဆိုချက်နှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ရန် chi-square goodness-of-fit စမ်းသပ်မှုပြုလုပ်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါမည်။
အဆင့် 1: ဒေတာကိုထည့်ပါ။
ပထမဦးစွာ ကျွန်ုပ်တို့သည် နေ့စဥ်မျှော်လင့်ထားသော ဖောက်သည်အရေအတွက်နှင့် နေ့စဥ်စောင့်ကြည့်လေ့လာထားသော ဖောက်သည်အရေအတွက်အတွက် ဒေတာတန်ဖိုးများကို ထည့်သွင်းပါမည်။ Stat ကိုနှိပ်ပြီး EDIT ကို နှိပ်ပါ။ ကော်လံ L1 ရှိ သတိပြုမိသော ဖောက်သည်အရေအတွက်အတွက် အောက်ပါတန်ဖိုးများနှင့် ကော်လံ L2 ရှိ မျှော်မှန်းထားသော ဖောက်သည်အရေအတွက်အတွက် တန်ဖိုးများကို ထည့်သွင်းပါ-
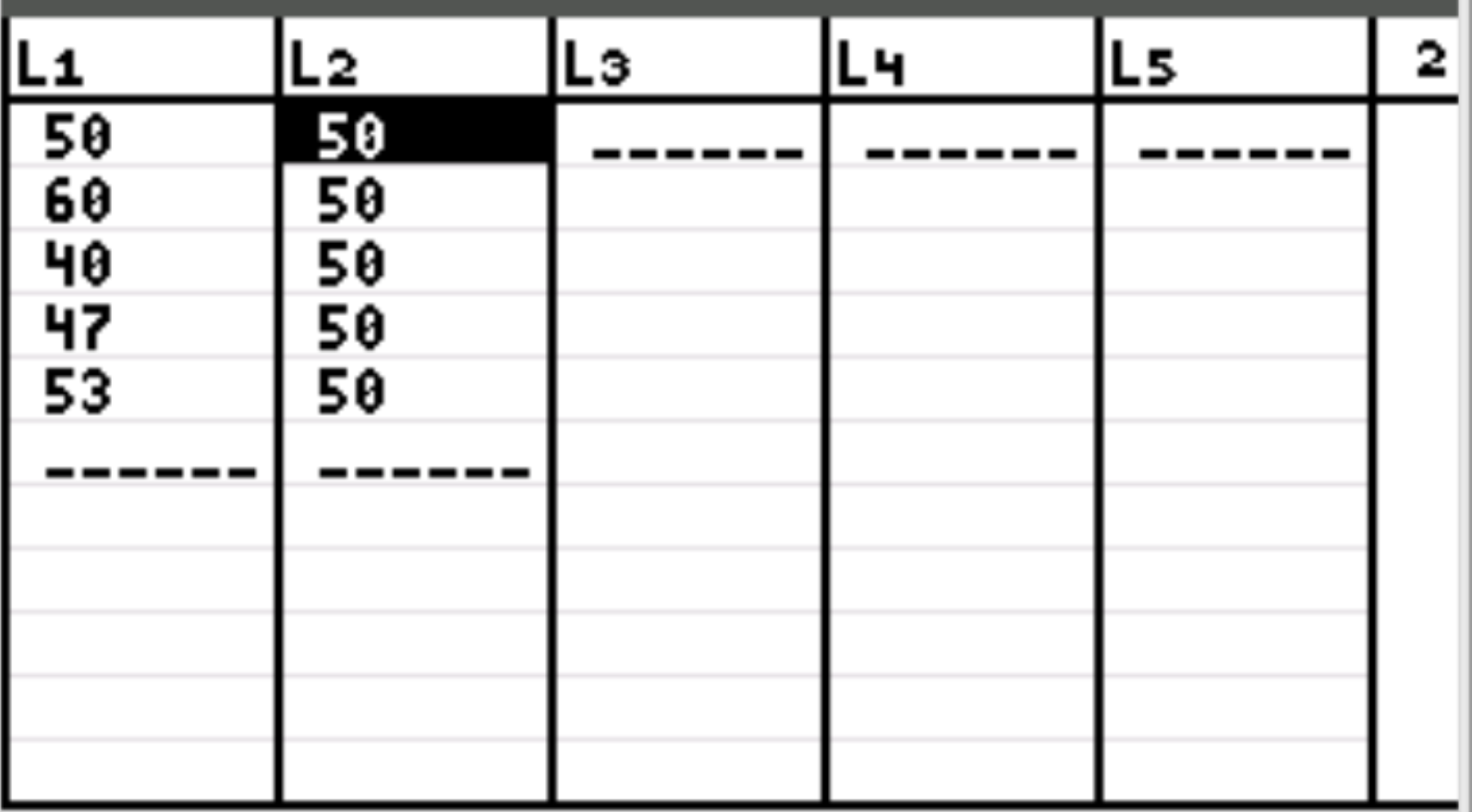
မှတ်ချက်- စုစုပေါင်း ဖောက်သည် 250 ရှိခဲ့သည်။ ဒါကြောင့် စတိုးဆိုင်ပိုင်ရှင်က တစ်နေ့ကို ဖောက်သည်အရေအတွက် ညီတူညီမျှ ဆိုင်ထဲကို ဝင်ဖို့ မျှော်လင့်ထားတယ်ဆိုရင် ဒါဟာ တစ်ရက်ကို ဖောက်သည် 50 ဖြစ်မှာပါ။
အဆင့် 2- chi-square goodness-of-fit စမ်းသပ်မှု ပြုလုပ်ပါ။
ထို့နောက်၊ ကျွန်ုပ်တို့သည် chi-square ကောင်းမွန်မှု-of-fit စမ်းသပ်မှုကို လုပ်ဆောင်ပါမည်။ Stat ကိုနှိပ်ပြီး TESTS သို့ ရွှေ့ပါ။ ထို့နောက် X 2 GOF-Test သို့ဆင်းပြီး Enter နှိပ်ပါ။
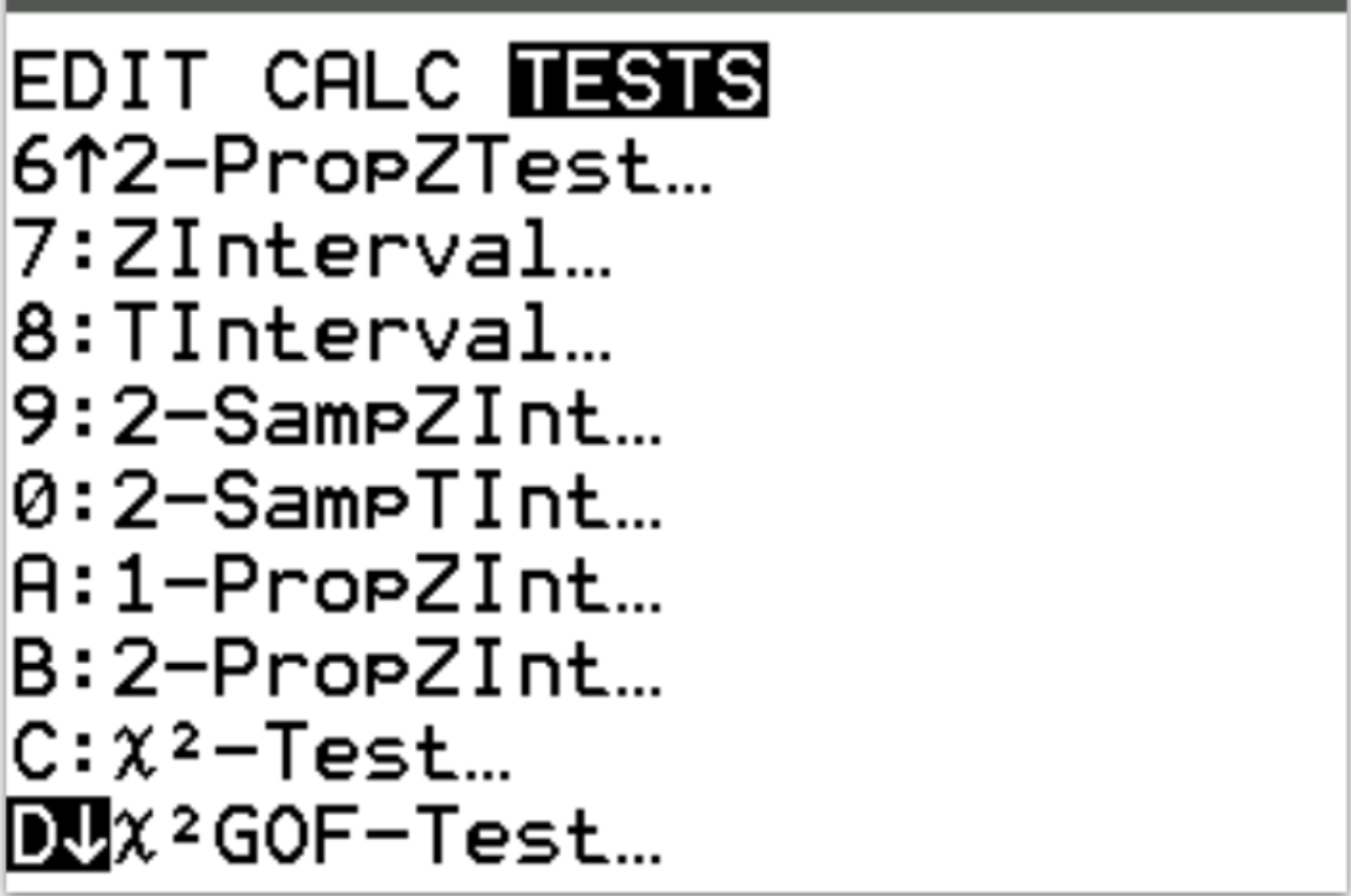
Observed အတွက် L1 စာရင်းကို ရွေးပါ။ မျှော်လင့်ထားသည့် အတွက်၊ L2 စာရင်းကို ရွေးပါ။ df (လွတ်လပ်မှုဒီဂရီအတွက်) #categories – 1 ကိုရိုက်ထည့်ပါ။ ကျွန်ုပ်တို့တွင် 5-1 = 4 ရှိသည်။ ထို့နောက် Calculate ကို အသားပေး၍ Enter နှိပ်ပါ။
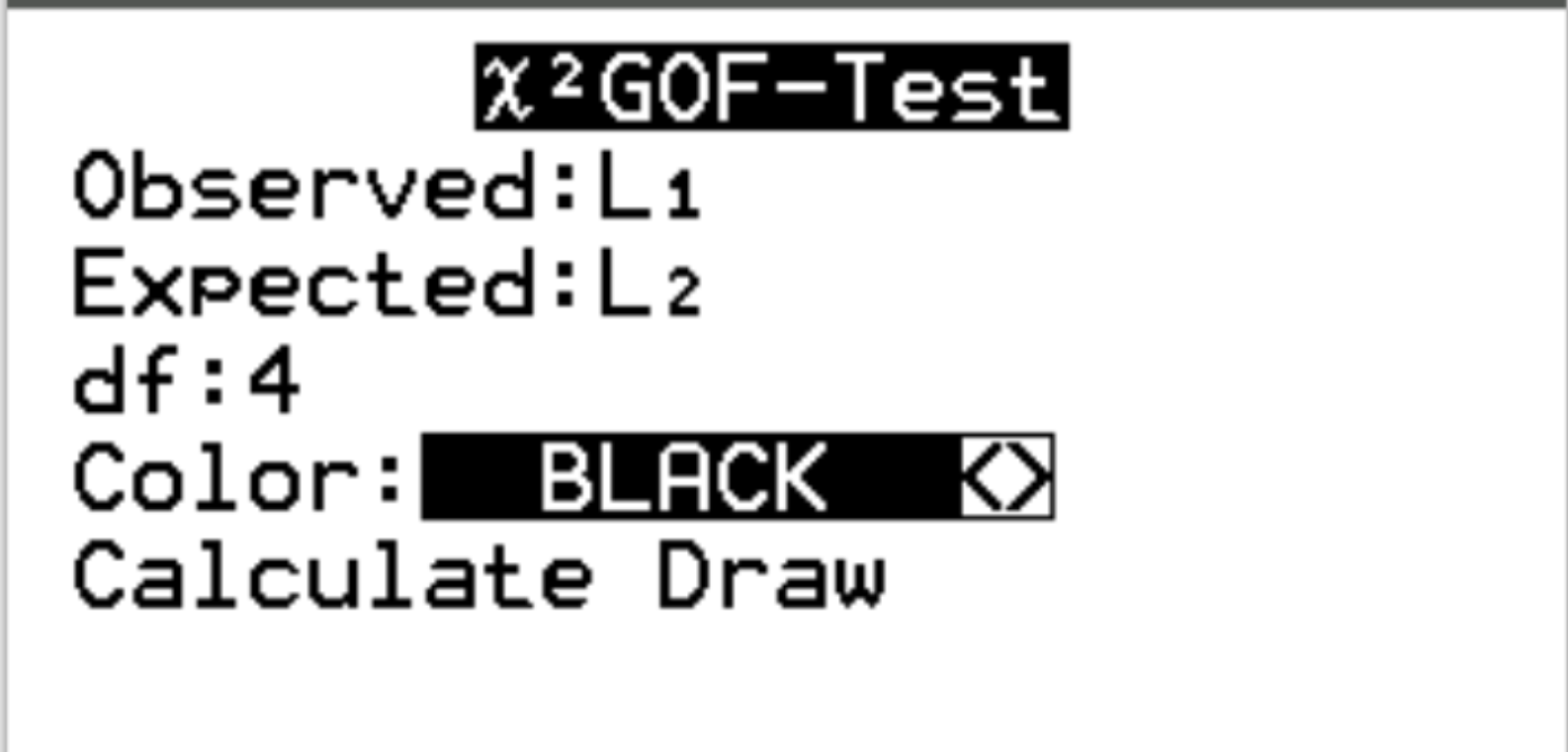
အောက်ပါ output သည် အလိုအလျောက် ပေါ်လာလိမ့်မည်-

အဆင့် 3- ရလဒ်များကို ဘာသာပြန်ပါ။
စစ်ဆေးမှုအတွက် X2 စမ်းသပ်မှုကိန်းဂဏန်းသည် 4.36 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် 0.3595 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဆိုလိုသည်မှာ စတိုးဆိုင်ပိုင်ရှင်မှ တင်ပြသော ဖောက်သည်များ၏ စစ်မှန်သော ဖြန့်ဖြူးမှုသည် ကွဲလွဲကြောင်း ပြောရန် လုံလောက်သော အထောက်အထား မရှိဟု ဆိုလိုပါသည်။