ရာခိုင်နှုန်းများ (စာရင်းအင်းများ)

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ရာခိုင်နှုန်းတစ်ခုသည် မည်သည့်အရာဖြစ်သည်နှင့် ၎င်းကို တွက်ချက်ပုံကို ရှင်းပြထားသည်။ ဖြေရှင်းနိုင်သော ရာခိုင်နှုန်းများလေ့ကျင့်ခန်းများကို သင်တွေ့နိုင်မည်ဖြစ်ပြီး ထို့အပြင်၊ သင်၏ဒေတာနမူနာ၏ မည်သည့်ရာခိုင်နှုန်းမဆိုကို အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် တွက်ချက်နိုင်မည်ဖြစ်သည်။

ရာခိုင်နှုန်းဆိုတာဘာလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင် ရာခိုင်နှုန်းများဆိုသည်မှာ မှာယူထားသောဒေတာအစုအဝေးကို အပိုင်းတစ်ရာစီခွဲထားသော တန်ဖိုးများဖြစ်သည်။ ထို့ကြောင့်၊ ရာခိုင်နှုန်းတစ်ခုသည် ဒေတာအစုတစ်ခု၏ ရာခိုင်နှုန်းတစ်ခုကျနေသည့် အောက်တန်ဖိုးကို ညွှန်ပြသည်။

ဥပမာအားဖြင့်၊ 35th ရာခိုင်နှုန်းတန်ဖိုးသည် လေ့လာတွေ့ရှိထားသည့်ဒေတာ၏ 35% ထက် မြင့်မားသော်လည်း ကျန်ဒေတာများထက် နိမ့်သည်။

Percentile များကို စာလုံးအကြီး P ဖြင့် ကိုယ်စားပြုပြီး ရာခိုင်နှုန်းအညွှန်းကိန်း၊ ဆိုလိုသည်မှာ 1st ရာခိုင်နှုန်းသည် P _1၊ 40th ရာခိုင်နှုန်းသည် P _40၊ 79th percentile သည် P ₇₉ စသည်တို့ဖြစ်သည်။

👉 မည်သည့်ဒေတာအတွဲ၏ ရာခိုင်နှုန်းများကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

အလားတူ၊ ရာခိုင်နှုန်းများသည် quartiles၊ quintiles နှင့် deciles တို့နှင့်အတူ ဗဟိုမဟုတ်သော အနေအထားကို တိုင်းတာခြင်းဖြစ်သည်။ ကျွန်ုပ်တို့၏ဝဘ်ဆိုဒ်တွင် ဤပမာဏအမျိုးအစားတစ်ခုစီ၏ အဓိပ္ပါယ်ကို သင်စစ်ဆေးနိုင်ပါသည်။

ကလေး၏ကိုယ်အလေးချိန်နှင့် အရပ်အမြင့်ကို အခြားကလေးများ၏ စံတန်ဖိုးများနှင့် နှိုင်းယှဉ်ရန် မှတ်သားထားသင့်သည်၊ အကြောင်းမှာ ကြီးထွားမှုဇယားများသည် ကလေးကြီးထွားမှုမှန်ကန်သည်ဖြစ်စေ မကြီးထွားသည်ဖြစ်စေ ဆုံးဖြတ်ရန် အထောက်အကူဖြစ်စေသော ကြီးထွားမှုဇယားများ ရှိနေသောကြောင့် သတိပြုသင့်သည်။ . .

ရာခိုင်နှုန်း တွက်ချက်နည်း

ကိန်းဂဏန်းအချက်အလက်စီးရီး တစ်ခု၏ ရာခိုင်နှုန်းတစ်ခု၏ အနေအထားကို တွက်ချက် ရန်၊ သင်သည် ဒေတာစုစုပေါင်း၏ ကိန်းဂဏန်းများ၏ ပေါင်းလဒ်နှင့် တစ်ရာခိုင်နှုန်းကို မြှောက်ပြီး ရလဒ်ကို ရာဂဏန်းဖြင့် ပိုင်းခြားရမည်ဖြစ်သည်။

ထို့ကြောင့် ရာခိုင်နှုန်းပြည့်ဖော်မြူလာ မှာ-

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ကျေးဇူးပြု၍ သတိပြုပါ- ဤဖော်မြူလာသည် ကျွန်ုပ်တို့အား ရာခိုင်နှုန်းအလိုက် အနေအထားကို ပြောပြသည်၊ သို့သော် ၎င်း၏တန်ဖိုးကို မဟုတ်ပါ။ ရာခိုင်နှုန်းသည် ဖော်မြူလာမှရရှိသော အနေအထားတွင်ရှိသော အချက်အလက်ဖြစ်လိမ့်မည်။

သို့သော်၊ တစ်ခါတစ်ရံတွင် ဤဖော်မြူလာ၏ရလဒ်သည် ကျွန်ုပ်တို့အား ဒဿမ နံပါတ်တစ်ခုပေးလိမ့်မည်၊ ထို့ကြောင့် ရလဒ်သည် ဒဿမကိန်းဖြစ်ခြင်း ရှိ၊ မရှိအပေါ် မူတည်၍ အမှုနှစ်ခုကို ခွဲခြားရပါမည်-

ဖော်မြူလာ၏ရလဒ်သည် ဒဿမအပိုင်းမရှိသော ဂဏန်းများ ဖြစ်ပါက၊ ရာခိုင်နှုန်းသည် အထက်ဖော်မြူလာမှပေးဆောင်သည့် အနေအထားရှိ ဒေတာနှင့် ကိုက်ညီပါသည်။
ဖော်မြူလာရလဒ်သည် ဒဿမအပိုင်းတစ်ခုပါရှိသော ဂဏန်း တစ်ခုဖြစ်ပါက၊ အတိအကျ ရာခိုင်နှုန်းတန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$P=x_i+d\cdot (x_{i+1}-x_i)$

x _i နှင့် x _i+1 သည် ပထမဖော်မြူလာမှရရှိသော နံပါတ်များကြားရှိ နံပါတ်များဖြစ်ပြီး d သည် ပထမဖော်မြူလာမှရရှိသော ဂဏန်းများ၏ ဒသမအပိုင်းဖြစ်သည်။

နည်းလမ်းသည် အဆင့်များစွာပါ၀င်သောကြောင့် ကိန်းဂဏန်းနမူနာတစ်ခု၏ ရာခိုင်နှုန်း သို့မဟုတ် လူဦးရေကိုရှာဖွေခြင်းသည် ရှုပ်ထွေးသည်ဟု ယခု သင်ထင်ကောင်းထင်နိုင်သော်လည်း ၎င်းမှာ အမှန်တကယ်လွယ်ကူပါသည်။ အောက်ဖော်ပြပါ ခိုင်မာသော ဥပမာနှစ်ခုကို ဖတ်ရှုပြီး ၎င်းကို သင်ပိုမိုနားလည်လာမည်မှာ သေချာပါသည်။

မှတ်ချက် – သိပ္ပံပညာအသိုက်အဝန်းသည် ရာခိုင်နှုန်းများကို တွက်ချက်နည်းနှင့်ပတ်သက်၍ ပြီးပြည့်စုံသောသဘောတူညီချက်မရသေးသောကြောင့် အနည်းငယ်ကွဲပြားကြောင်းရှင်းပြထားသည့် ကိန်းဂဏန်းစာရင်းစာအုပ်ကို သင်ရှာတွေ့နိုင်ပါသည်။

ရာခိုင်နှုန်းတွက်ချက်မှု ဥပမာများ

နမူနာတစ်ခု၏ ရာခိုင်နှုန်းများကို ရှာဖွေနည်း၏ ရှင်းလင်းချက်တွင် အထက်တွင် သင်တွေ့ခဲ့သည့်အတိုင်း၊ တွက်ချက်မှုသည် ပထမဖော်မြူလာ၏ ရလဒ်သည် ဒဿမ ဟုတ်မဟုတ် တွက်ချက်မှုအပေါ် မူတည်၍ ကွဲပြားသည်။ ထို့ကြောင့် အောက်တွင် ဖြေရှင်းထားသော ဥပမာနှစ်ခုကို တွေ့ရမည်ဖြစ်ပြီး အမှုတစ်ခုစီအတွက် တစ်ခုဖြစ်သည်။

ဥပမာ ၁

အောက်ပါဇယားတွင်ပြထားသည့်ဒေတာမှ 1st၊ 43 နှင့် 89th ရာခိုင်နှုန်းများကိုတွက်ချက်ပါ။

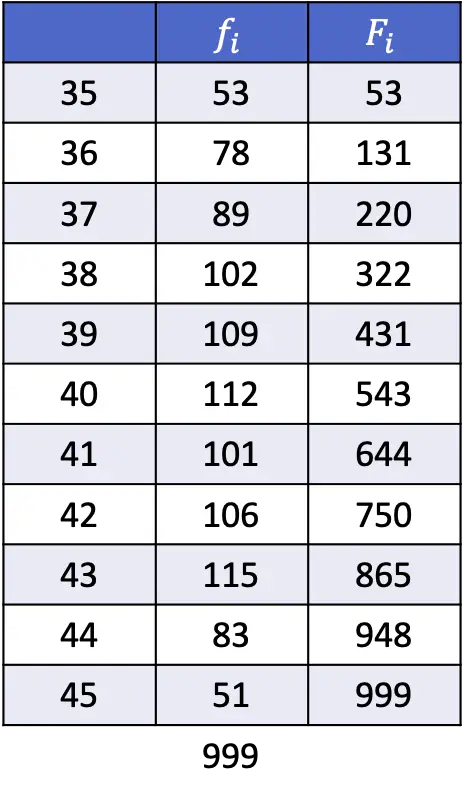
ယခင်အပိုင်းတွင် ရှင်းပြထားသည့်အတိုင်း ရာခိုင်နှုန်းတစ်ခု၏ အနေအထားကို ရှာဖွေရန် ဖော်မြူလာမှာ-

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ဤကိစ္စတွင်၊ ဤလေ့ကျင့်ခန်းအတွက်နမူနာအရွယ်အစားသည် 999 ကိန်းဂဏန်းအချက်အလက်များဖြစ်သောကြောင့်၊ ပထမရာခိုင်နှုန်းကိုတွက်ချက်ရန် 999 ကို n နှင့် 1 k အတွက် အစားထိုးရန်လိုအပ်ပါသည်။

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

ထို့ကြောင့် 1st percentile သည် 10 ထက် ပိုများသော စုစည်းမှု ပကတိအကြိမ်ရေဖြစ်ပြီး၊ ဤအခြေအနေတွင် 35 သည် 53 ရှိသော absolute frequency ဖြစ်သောကြောင့်ဖြစ်သည်။

43rd percentile ကို ဆုံးဖြတ်ရန် တူညီသော ဖော်မြူလာကို အသုံးပြုရမည်ဖြစ်သော်လည်း၊ ယခုတစ်ကြိမ်တွင် k ကို 43 ဖြင့် အစားထိုးပါသည်။

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

430 အထက်ရှိ အကြွင်းမဲ့ တိုးပွားနှုန်းသည် ဒေတာ 39 ၏ 431 ဖြစ်ပြီး၊ ထို့ကြောင့် 43rd ရာခိုင်နှုန်းသည် 39 နှင့် ညီမျှသည်။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် 89th ရာခိုင်နှုန်းရရှိရန် တူညီသောဖော်မြူလာကို အသုံးပြုသည်-

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

တန်ဖိုး 44 ၏ ပကတိကြိမ်နှုန်းသည် 948 ဖြစ်ပြီး ၎င်းသည် 890 ထက် ချက်ချင်းကြီးသည်။ ထို့ကြောင့် 89th ရာခိုင်နှုန်းသည် 44 ဖြစ်သည်။

ဥပမာ ၂

အောက်ပါဒေတာစီးရီးများ၏ 35th နှင့် 67th ရာခိုင်နှုန်းကို ရှာပါ-

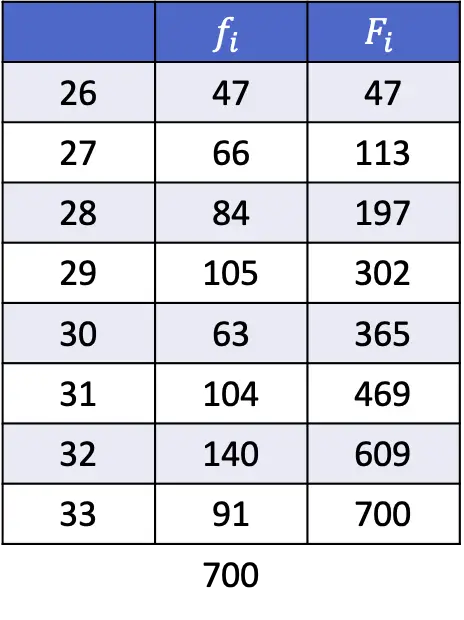
ဤလေ့ကျင့်ခန်းတွင် ကျွန်ုပ်တို့ ပိုမိုတွက်ချက်မှုများ ပြုလုပ်ရမည်ဖြစ်ပြီး နိယာမသည် အတူတူပင်ဖြစ်သည်- ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ စကားရပ်ဖြင့် ရာခိုင်နှုန်းရာခိုင်နှုန်းကို တွက်ချက်ရမည်ဖြစ်သည်။

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

ထို့ကြောင့် 35th ရာခိုင်နှုန်းကို တွက်ချက်ရန်အတွက် k ကို 35 နှင့် n ကို ဒေတာစုစုပေါင်းအရေအတွက်အားဖြင့် 700 ၊ ဆိုလိုသည်မှာ –

$\cfrac{35\cdot (700+1)}{100}=245,35$

သို့သော် ဤအကြိမ်တွင် ကျွန်ုပ်တို့သည် ဖော်မြူလာမှ ဒဿမဂဏန်းကို ရရှိသောကြောင့် ရာခိုင်နှုန်းအတိအကျတန်ဖိုးကို တွက်ချက်ရန် အောက်ပါ အက္ခရာသင်္ချာအသုံးအနှုန်းကို အသုံးပြုရန် လိုအပ်ပါသည်။

$P=x_i+d\cdot (x_{i+1}-x_i)$

ပထမဖော်မြူလာမှပေးသောနံပါတ်သည် 245.35 ဖြစ်ပြီး၊ ထို့ကြောင့် 35th percentile သည် ရာထူး 245 နှင့် 246 ကြားဖြစ်ပြီး တန်ဖိုး 29 နှင့် 29 အသီးသီးနှင့် သက်ဆိုင်သည်။ ထို့ကြောင့် x _i သည် 29 ဖြစ်ပြီး x _i+1 သည် 29 ဖြစ်ပြီး d သည် 0.35 ဖြစ်သည့် ဂဏန်း၏ ဒဿမအပိုင်းနှင့် ထိုက်တန်သည်။

$P_{35}=29+0,35\cdot (29-29)=29$

67th ရာခိုင်နှုန်းကိုရှာရန်၊ ကျွန်ုပ်တို့သည် တူညီသောနည်းလမ်းကို အသုံးပြုရန်လိုအပ်သည်။ ပထမဦးစွာ ကျွန်ုပ်တို့သည် ရာခိုင်နှုန်းအနေအထားကို တွက်ချက်သည်-

$\cfrac{67\cdot (700+1)}{100}=469,67$

ရလဒ်နံပါတ် 469.67 သည် ရာထူး 469 နှင့် 470 အကြားရှိ၊ 31 နှင့် 32 တန်ဖိုးများဖြစ်ကြောင်း ညွှန်ပြသည်။ ထို့ကြောင့်၊ ရာခိုင်နှုန်းအတိအကျတန်ဖိုးကိုရှာဖွေရန် လုပ်ငန်းစဉ်အတွင်းရှိ ဒုတိယဖော်မြူလာကို ကျွန်ုပ်တို့အသုံးပြုသည်-

$P_{67}=31+0,67\cdot (32-31)=31,67$

ရာခိုင်နှုန်းဂဏန်းတွက်စက်

အောက်ပါဂဏန်းတွက်စက်တွင် သင်တွက်ချက်လိုသော ကိန်းဂဏန်းအချက်အလက်အစုံနှင့် ရာခိုင်နှုန်းအရေအတွက်ကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာတွင် ရာခိုင်နှုန်းများ

ဒေတာများကို အုပ်စုများအဖြစ် အုပ်စုဖွဲ့လိုက်သောအခါ ရာခိုင်နူန်းများကို တွက်ချက် ရန်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ အုပ်စု သို့မဟုတ် အတန်းထဲတွင် ရာခိုင်နှုန်းပါရှိသည့် အတန်းကို ရှာဖွေရန် လိုအပ်သည်-

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ထို့ကြောင့် ရာခိုင်နှုန်းသည် ယခင်ဖော်ပြချက်တွင်ရရှိသော ကိန်းဂဏန်းထက် အကြွင်းမဲ့ ကြိမ်နှုန်းသည် ချက်ချင်းကြီးနေသည့် ကြားကာလတွင် ဖြစ်လိမ့်မည်။

ရာခိုင်နှုန်းအလိုက် ပိုင်ဆိုင်သည့် ကြားကာလကို ကျွန်ုပ်တို့ သိရှိပြီးသည်နှင့်၊ ရာခိုင်နှုန်းအတိအကျတန်ဖိုးကို ရှာဖွေရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည်။

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

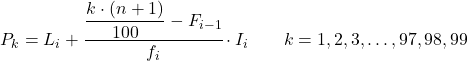
ရွှေ-

L _i သည် ရာခိုင်နှုန်းအလိုက် တည်ရှိနေသည့် ကြားကာလ၏ အနိမ့်ဆုံးကန့်သတ်ချက်ဖြစ်သည်။
n သည် လေ့လာတွေ့ရှိချက် စုစုပေါင်း အရေအတွက်ဖြစ်သည်။
F _i-1 သည် ယခင်ကြားကာလ၏ ပကတိအကြိမ်အရေအတွက်ဖြစ်သည်။
f _i သည် ရာခိုင်နှုန်းအလိုက် တည်ရှိနေသည့် ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
ငါ _i သည် ရာခိုင်နှုန်းအကွာအဝေး၏ အကျယ်ဖြစ်သည်။

အောက်တွင် ဒေတာများကို ကြားကာလများတွင် ဖော်ပြသည့်အခါ ရာခိုင်နှုန်းအလိုက် ရရှိရန် လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။ အတိအကျအားဖြင့်၊ 29th၊ 52nd နှင့် 98th ရာခိုင်နှုန်းများကို တွက်ချက်သည်။

ဤနမူနာရှိ ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသောကြောင့် ရာခိုင်နူန်းများကို ဆုံးဖြတ်ရန် အဆင့်နှစ်ဆင့်ကို လုပ်ဆောင်ရန် လိုအပ်သည်- ပထမဦးစွာ ကျွန်ုပ်တို့သည် ရာခိုင်နှုန်းအလိုက် ကျရောက်သည့် ကြားကာလကို ရှာဖွေရန် လိုအပ်ပြီး ရာခိုင်နှုန်းအတိအကျတန်ဖိုးကို တွက်ချက်ရန်အတွက် ဖော်မြူလာကို အသုံးပြုပါ။ ရာခိုင်နှုန်း။

ထို့ကြောင့်၊ 29th percentile ၏ အနေအထားကို အောက်ပါ စကားရပ်ဖြင့် ရှာတွေ့သည် ။

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

Percentile interval သည် 145.29 ထက် ချက်ချင်းကြီးသော စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းဖြစ်လိမ့်မည်၊ ယင်းတွင် ဤအခြေအနေတွင် ကြားကာလသည် [350.375) ဖြစ်သည့် စုဆောင်းမှု absolute frequency သည် 175 ဖြစ်သည်။ Percentile ကြားကာလကို ကျွန်ုပ်တို့သိသည်နှင့်၊ ၎င်းကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုပါသည်။ တန်ဖိုးအတိအကျ:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

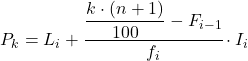
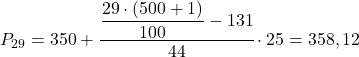
ယခု ကျွန်ုပ်တို့သည် 52nd ရာခိုင်နှုန်းကို တွက်ချက်ရန် တူညီသောလုပ်ငန်းစဉ်ကို ပြန်လုပ်ပါသည်။ ကျွန်ုပ်တို့သည် ၎င်း၏ကြားကာလကို ဦးစွာတွက်ချက်သည်-

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

၎င်း၏ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း (၂၉၈) သည် 260.52 အထက် ချက်ချင်းဖြစ်သောကြောင့် 52nd ရာခိုင်နှုန်းကြားကာလသည် [400.425) ဖြစ်သည်။ ထို့ကြောင့် ရာခိုင်နှုန်းအလိုက်တန်ဖိုးသည်-

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

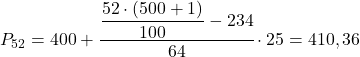
နောက်ဆုံးတွင်၊ 98th ရာခိုင်နှုန်းကိုတွေ့လိမ့်မည်။ အမြဲလိုလို၊ ကျွန်ုပ်တို့သည် ၎င်းတည်ရှိသည့် ကြားကာလကို ဦးစွာတွက်ချက်သည်-

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

ရာခိုင်နှုန်းအလိုက် တည်ရှိသည့် ကြားကာလကို ကျွန်ုပ်တို့ သိရှိသည်နှင့် ၎င်း၏တန်ဖိုးအတိအကျကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်ပါသည်။

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ရာခိုင်နှုန်းဆိုတာဘာလဲ။

ရာခိုင်နှုန်း တွက်ချက်နည်း

ရာခိုင်နှုန်းတွက်ချက်မှု ဥပမာများ

ဥပမာ ၁

ဥပမာ ၂

ရာခိုင်နှုန်းဂဏန်းတွက်စက်

အုပ်စုဖွဲ့ဒေတာတွင် ရာခိုင်နှုန်းများ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။