သေတ္တာနှင့် ပါးသိုင်းကွက်များ

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် box plot (သို့မဟုတ် boxplot) ဟုလည်းသိကြသော boxplot ကဘာလဲဆိုတာရှင်းပြထားသည်။ ဤစာရင်းအင်းပုံများ အမျိုးအစားများကို မည်ကဲ့သို့ပြုလုပ်ပုံနှင့် သေတ္တာတစ်လုံးနှင့် ပါးသိုင်းမွှေးပုံကြမ်းနှင့် ၎င်း၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်ကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်သည်။

သေတ္တာတစ်လုံးနှင့် ပါးသိုင်းမွှေးကွက်ဆိုသည်မှာ အဘယ်နည်း။

boxplot သို့မဟုတ် boxplot ဟုလည်း ခေါ်သည် ၊ သည် quartiles ကို အသုံးပြု၍ ကိန်းဂဏန်း အချက်အလက် အစုအဝေးကို အမြင်အားဖြင့် ကိုယ်စားပြုသည့် ဂရပ်တစ်ခု ဖြစ်သည်။

box နှင့် whisker plot ၏ အဓိကလက္ခဏာမှာ quartiles ၊ median ၊ extreme values နှင့် data ၏ outliers တို့ကို ညွှန်ပြသောကြောင့် ဒေတာစီးရီးများ၏ ပြန့်ကျဲမှုကို လျင်မြန်စွာမြင်ယောင်နိုင်စေပါသည်။

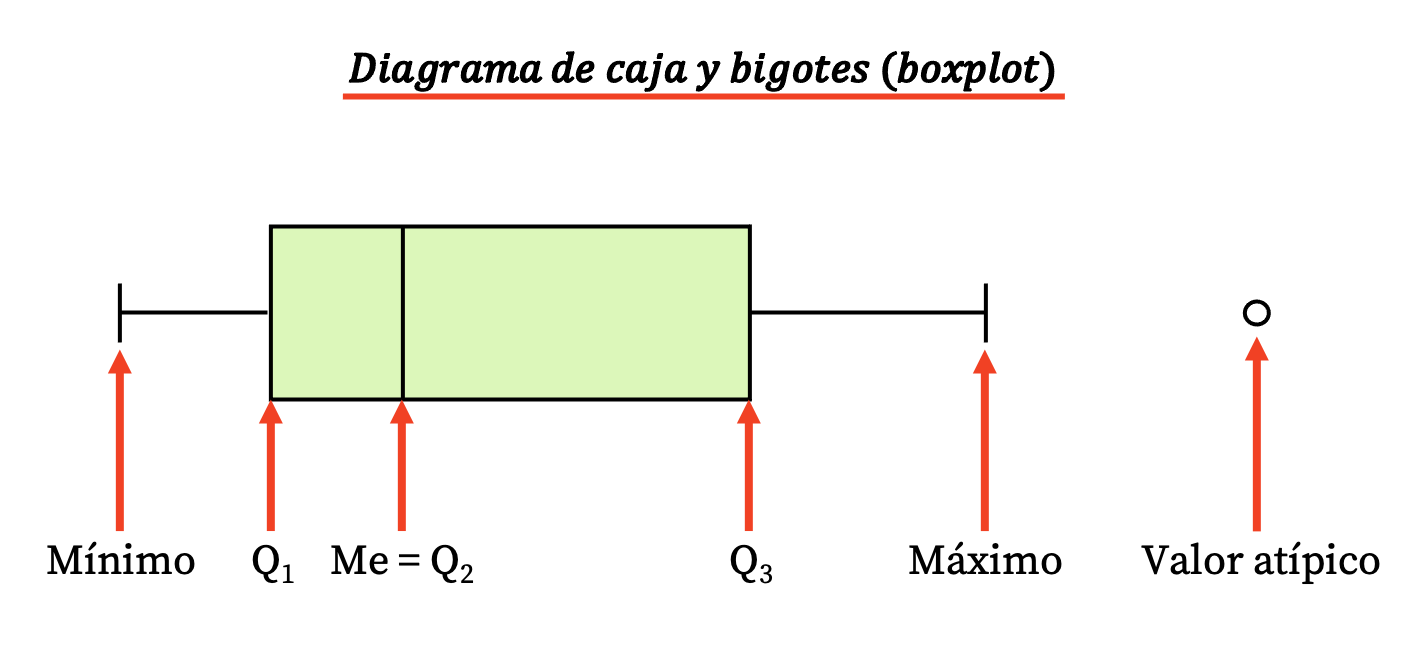
ထို့ကြောင့် ဤပုံကြမ်းအမျိုးအစားကို စတုဂံပုံသေတ္တာတစ်ခုနှင့် အောက်ပါတန်ဖိုးများ ထွက်ပေါ်လာသည့် လိုင်းအနည်းငယ် (သို့မဟုတ် ပါးသိုင်းမွှေး) ဖြင့် ဖွဲ့စည်းထားသည်။

အကွက်၏ နယ်နိမိတ်များသည် ပထမနှင့် တတိယ ကွာတားများ (Q ₁ နှင့် Q ₃ ) ကို ညွှန်ပြသည်။ အကွက်အတွင်းရှိ ဒေါင်လိုက်မျဉ်းသည် ပျမ်းမျှ (ဒုတိယ quartile _Q2 နှင့် ညီမျှသည်)။
ပါးသိုင်းမွှေးများ (သို့မဟုတ် လက်များ) ၏ ကန့်သတ်ချက်များသည် လွန်ကဲတန်ဖိုးများ ဖြစ်သည်၊ ဆိုလိုသည်မှာ ဒေတာစီးရီး၏ အနိမ့်ဆုံးတန်ဖိုးနှင့် အမြင့်ဆုံးတန်ဖိုးကိုဆိုလိုသည်။
ပါးသိုင်းမွှေးများ အပြင်ဘက်ရှိ အမှတ်များသည် အစွန်းအထင်းများ ဖြစ်သည် သို့မဟုတ် တစ်နည်းအားဖြင့် မှားယွင်းစွာ တိုင်းတာထားသော ဒေတာများ ဖြစ်သော ကြောင့် စာရင်းအင်းလေ့လာမှုတွင် ထည့်သွင်းစဉ်းစားရန် မသင့်ပါ။

တတိယနှင့် ပထမ quartile အကြား ခြားနားချက်မှာ interquartile အကွာအဝေး (သို့မဟုတ် interquartile range)၊ ကိန်းဂဏန်းဆိုင်ရာ ကွဲလွဲမှု၏ အခြားသော အတိုင်းအတာဖြစ်သည်ကို သတိပြုပါ။

Box နှင့် whisker ကွက်များသည် ကိန်းဂဏန်းကိန်းရှင်များကို နှိုင်းယှဉ်ရန်အတွက် အလွန်အသုံးဝင်ပါသည်။ သို့ရာတွင်၊ အမျိုးအစားအလိုက် ကိန်းရှင်များကို ကိုယ်စားပြုရန် ၎င်းသည် မသင့်လျော်ပါ။

Box နှင့် Whisker Plot ဖန်တီးနည်း

ဒေတာစီးရီးတစ်ခုမှ box နှင့် ပါးသိုင်းကွက်ကွက် (သို့မဟုတ် boxplot) ဖန်တီးရန်၊ အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

ကိန်းဂဏန်းအချက်အလက် ဥပမာများကို ခွဲထုတ်ပါ။
quartiles (Q ₁ ၊ Q ₂ နှင့် Q ₃ ) ကို တွက်ချက်ပြီး ပုံတွင်ပြထားသော အကွက်အဖြစ် ကိုယ်စားပြုသည်။ ပထမနှင့် တတိယမြောက် quartile များသည် box ၏ ကန့်သတ်ချက်များနှင့် ကိုက်ညီပြီး အလယ်အလတ် (ဒုတိယ quartile) ကို ကိုယ်စားပြုရန်အတွက် ၎င်း၏တန်ဖိုးတည်ရှိသည့် အကွက်အတွင်း မျဉ်းတစ်ကြောင်းဆွဲရပါမည်။
တတိယ quartile အနှုတ် ပထမ quartile နှင့် ညီမျှသည့် interquartile အပိုင်းအခြားကို တွက်ချက်ပါ။

$IQR=Q_3-Q_1$

ဖော်မြူလာများဖြစ်သည့် LI နှင့် LS တို့၏ လက်ခံနိုင်သောတန်ဖိုးများကို တွက်ချက်ပါ။

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

LI ထက်နည်းသောတန်ဖိုးများ သို့မဟုတ် LS ထက်ကြီးသောတန်ဖိုးများဖြစ်သည့် နမူနာအကွာအဝေးများကို ခွဲခြားသတ်မှတ်ပါ။ ဤတန်ဖိုးများကို ပါးသိုင်းမွှေးဘောင်အပြင်ဘက်တွင် အစက်များဖြင့် ကိုယ်စားပြုပါ။
LI နှင့် LS တို့ဖြင့် ဖွဲ့စည်းထားသော ကြားကာလတွင် အသေးငယ်ဆုံးတန်ဖိုးနှင့် အကြီးဆုံးတန်ဖိုးများဖြစ်သည့် လွန်ကဲတန်ဖိုးများကို ခွဲခြားသတ်မှတ်ပြီး ကိုယ်စားပြုသည်။ ဤတန်ဖိုးများသည် ပုံကြမ်းတွင် ပါးသိုင်းမွှေးနှစ်ချောင်း၏ အဆုံးကို ကိုယ်စားပြုသည်။

Box and Whisker Plot နမူနာ

box နှင့် whisker plot (သို့မဟုတ် boxplot) ၏ အဓိပ္ပါယ်နှင့် သီအိုရီကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် သဘောတရားကို ပိုမိုကောင်းမွန်စွာ နားလည်နိုင်ပြီး ဤစာရင်းအင်းကွက်အမျိုးအစားကို မည်သို့လုပ်ဆောင်သည်ကို ကြည့်ရှုရန် ခိုင်မာသော ဥပမာတစ်ခုအောက်တွင် သင်တွေ့ရပါမည်။

အောက်ပါစာရင်းအင်းဒေတာအစုံ၏ ကွက်လပ်တစ်ခုဆွဲပါ။

ဤကိစ္စတွင်၊ ဒေတာကို အသေးဆုံးမှ အကြီးဆုံးသို့ စီထားပြီးဖြစ်သောကြောင့် အပြောင်းအလဲများ မလိုအပ်ပါ။ မဟုတ်ပါက ကျွန်ုပ်တို့သည် နမူနာဒေတာကို ဦးစွာစီစစ်သင့်သည်။

ဒုတိယအနေဖြင့်၊ ကျွန်ုပ်တို့သည် နမူနာ၏ လေးပုံတစ်ပုံကို ထုတ်ယူပါသည်။

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ လေးပုံတစ်ပုံဂဏန်းတွက်စက်ကို ကြည့်ပါ။

quartile သုံးခုကို တွက်ချက်ပြီးသည်နှင့် quartile 3 အနှုတ် quartile 1 ကို နုတ်ခြင်းဖြင့် interquartile အပိုင်းအခြားကို ရှာတွေ့ပါသည်။

$IQR=Q_3-Q_1=4,66-4,06=0,6$

ယခု ကျွန်ုပ်တို့သည် LI နှင့် LS ကန့်သတ်ချက်များကို တွက်ချက်ပြီး ၎င်းတို့သည် ဒေတာကို ပုံမှန်ဟု ယူဆသည့် တန်ဖိုးများဖြစ်သည်။ ဒါကိုလုပ်ဖို့၊ အောက်ပါဖော်မြူလာတွေကို သုံးရပါမယ်။

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

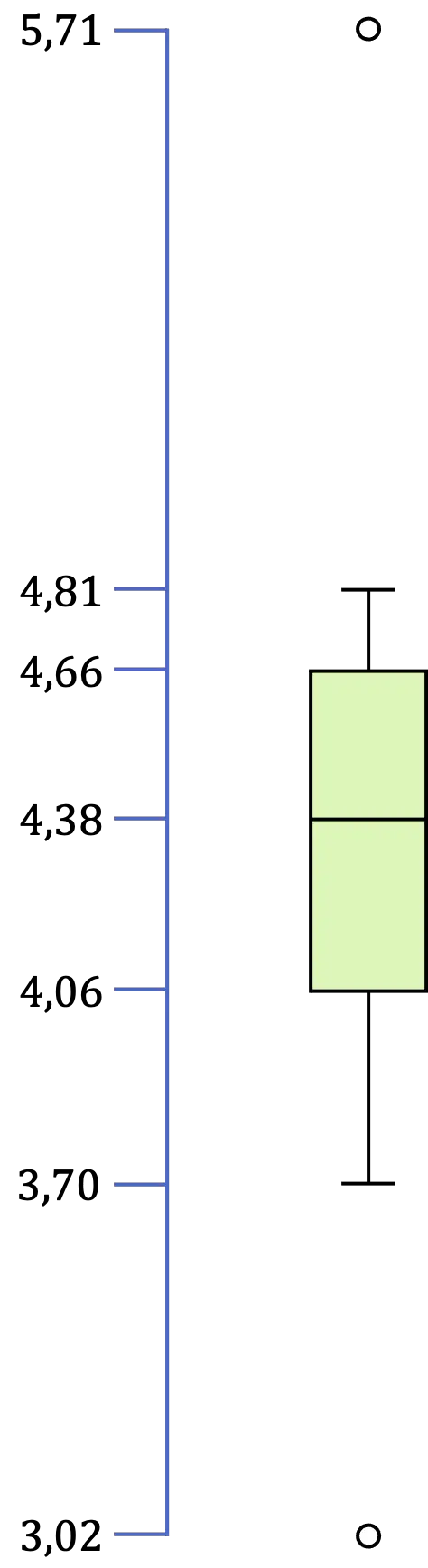
ထို့ကြောင့် ဤကိစ္စတွင် ကျွန်ုပ်တို့တွင် 3.02 သည် 3.16 ထက်နည်းသောကြောင့် 5.71 သည် 5.56 ထက်ကြီးသောကြောင့်ဖြစ်သည်။

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

နောက်ဆုံးတွင်၊ ၎င်းသည် ကြားကာလ [LI,LS] အတွင်းရှိ ဒေတာအားလုံး၏ အနိမ့်ဆုံးနှင့် အမြင့်ဆုံးဖြစ်သည့် လွန်ကဲတန်ဖိုးများကို ခွဲခြားသတ်မှတ်ရန် ကျန်နေသေးသည်။ ထို့ကြောင့် ကျွန်ုပ်တို့၏ဥပမာတွင် အနိမ့်ဆုံးတန်ဖိုးမှာ 3.70 ဖြစ်ပြီး အမြင့်ဆုံးတန်ဖိုးမှာ 4.81 ဖြစ်သည်။

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် box နှင့် whisker plot ၏တန်ဖိုးအားလုံးကိုဖော်ထုတ်ပြီးသည်နှင့်ကျန်ရှိနေသေးသည်အားလုံးကိုဂရပ်ဖစ်ကိုယ်စားပြုမှုပြုလုပ်ရန်ဖြစ်သည်-

သေတ္တာတစ်လုံးနှင့် ပါးသိုင်းမွှေးကွက်ကို ဘာအတွက်အသုံးပြုသနည်း။

နောက်ဆုံးအနေနဲ့၊ ဘောက်စ်နဲ့ ပါးသိုင်းကွက်ကွက် (သို့မဟုတ် boxplot) ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်ရမလဲဆိုတာ ကြည့်ကြရအောင်။

ထင်ရှားသည်မှာ၊ အကွက်နှင့် ပါးသိုင်းကွက်ကွက်များသည် ဒေတာစီးရီးတစ်ခု၏ quartiles၊ interquartile range၊ median၊ extreme values နှင့် outliers တို့ကို လျင်မြန်စွာသိရှိရန်အတွက် အလွန်အသုံးဝင်သောကြောင့်၊ ဤစာရင်းအင်းဆိုင်ရာတိုင်းတာမှုများကို ရိုးရိုးရှင်းရှင်းဖြင့် ဖော်ထုတ်နိုင်ပါသည်။

ထို့အပြင်၊ ၎င်းသည် ဒေတာအစုတစ်ခုလုံးကို အမြင်အားဖြင့် ကိုယ်စားပြုသောကြောင့် ကိန်းဂဏန်းနမူနာ၏ အချိုးညီမှုကို ခွဲခြမ်းစိတ်ဖြာရန် အကွက်နှင့် ပါးသိုင်းကွက်ကို အသုံးပြုထားသည်။ အလယ်အလတ်သည် အကွက်၏ အလယ်တွင် မရှိပါက၊ နမူနာသည် အချိုးမညီဟု ဆိုလိုသည်။

အလားတူ၊ အချိန်တိုအတွင်း အမြင့်ဆုံးတန်ဖိုး၊ အနိမ့်ဆုံးတန်ဖိုးနှင့် အလယ်အလတ်တန်ဖိုးများကို အချိန်တိုအတွင်း မြင်နိုင်စေသောကြောင့် စတော့ဈေးကွက်တွင် boxplots များကို ကျယ်ကျယ်ပြန့်ပြန့်အသုံးပြုကြသည်။ အချိန်နဲ့အမျှ ပိုမြန်တဲ့ ဆုံးဖြတ်ချက်တွေချပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။