အလယ်အလတ်ကွာခြားမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် အဓိပ္ပါယ်သွေဖည်ခြင်းဆိုသည်မှာ မည်ကဲ့သို့ တွက်ချက်သည်ကို ရှင်းပြထားသည်။ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ခြင်း၏ ခိုင်မာသော ဥပမာများကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ သင်သည် အွန်လိုင်း ဂဏန်းတွက်စက်ကို အသုံးပြု၍ မည်သည့် ကိန်းဂဏန်းအချက်အလက်များ၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

အဓိပ္ပါယ်သွေဖည်ခြင်းဆိုသည်မှာ အဘယ်နည်း။

Mean deviation , mean absolute deviation ဟုလည်း ခေါ်သည် ၊ သည် ကိန်းဂဏန်း ကွဲလွဲမှု ၏ အတိုင်းအတာ တစ်ခု ဖြစ်သည်။

ဒေတာအစုတစ်ခု၏ ပျမ်းမျှသွေဖည်မှုသည် ပကတိသွေဖည်မှုများ၏ပျမ်းမျှဖြစ်သည် ။ ထို့ကြောင့်၊ ပျမ်းမျှသွေဖည်မှုသည် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားသော ဂဏန်းသင်္ချာပျမ်းမျှမှ ဒေတာပစ္စည်းတစ်ခုစီ၏ သွေဖည်မှုပေါင်းလဒ်နှင့် ညီမျှသည်။

တစ်နည်းအားဖြင့် ပျမ်းမျှသွေဖည်မှုအတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

👉 မည်သည့်ဒေတာအတွဲ၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

စာရင်းဇယားများတွင် ပျမ်းမျှသွေဖည်မှုကို mean absolute deviation ဟုခေါ်သည်။

ပျမ်းမျှသွေဖည်ခြင်း၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်ကို အောက်ပါအတိုင်း လုပ်ဆောင်သည်- ပျမ်းမျှသွေဖည်မှုတန်ဖိုး ပိုများလေ၊ ဒေတာသည် ပျမ်းမျှအားဖြင့် ဂဏန်းသင်္ချာပျမ်းမျှထက် ပိုကွာသည်ဟု ဆိုလိုသည်။ ဆန့်ကျင်ဘက်အားဖြင့်၊ ပျမ်းမျှသွေဖည်မှု နိမ့်လေ၊ တန်ဖိုး နီးကပ်လေဖြစ်သည်။ data က။ ထို့ကြောင့် ပျမ်းမျှသွေဖည်မှုသည် ဒေတာစီးရီးတစ်ခု၏ ကွဲလွဲမှုကို ဖော်ပြသည်။

ဖြန့်ဝေသတ်မှတ်ထားသော အခြားအတိုင်းအတာများမှာ အပိုင်းအခြား၊ ကွာတားအကွာအဝေး၊ စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု)၊ ကွဲလွဲမှု နှင့် ကွဲလွဲမှု၏ကိန်းဂဏန်းများဖြစ်သည်။

ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်နည်း

ဒေတာစီးရီးတစ်ခု၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-

ကိန်းဂဏန်းအချက်အလက်အစုံ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ပါ ။
ဒေတာနှင့် ပျမ်းမျှအကြား ကွာခြားချက်၏ ပကတိတန်ဖိုးအဖြစ် သတ်မှတ်ထားသော ဒေတာအမှတ်တစ်ခုစီ၏ သွေဖည်မှုကို တွက်ချက်ပါ။
ယခင်အဆင့်တွင် တွက်ချက်ထားသော ကွဲပြားမှုအားလုံးကို ပေါင်းထည့်ပါ။
အချက်အလက် စုစုပေါင်း အရေအတွက်ဖြင့် ပိုင်းပါ။ ရရှိသောရလဒ်သည် ဒေတာစီးရီး၏ ပျမ်းမျှသွေဖည်မှုဖြစ်သည်။

အချုပ်အားဖြင့်၊ ပျမ်းမျှသွေဖည်မှုကို ရှာဖွေရန် အသုံးပြုရမည့် ဖော်မြူလာမှာ-

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ခြင်း ဥပမာ

ပျမ်းမျှသွေဖည်ခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့်၊ အောက်တွင် ကိန်းဂဏန်းနမူနာတစ်ခု၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ရာတွင် အဆင့်ဆင့်ဖြေရှင်းထားသော ဥပမာတစ်ခုဖြစ်သည်။ ဤနည်းအားဖြင့် သင်သည် ပျမ်းမျှသွေဖည်မှုကို မည်သို့ရယူရမည်ကို ကောင်းစွာနားလည်နိုင်မည်ဖြစ်သည်။

အကဲခတ်သူတစ်ဦးသည် လွန်ခဲ့သည့်နှစ်အတွင်း ကုမ္ပဏီတစ်ခု၏ စီးပွားရေးရလဒ်များကို လေ့လာပြီး ထိုနှစ်၏သုံးလပတ်တစ်ခုစီတွင် ကုမ္ပဏီမှရရှိသောအမြတ်ငွေများ- ဒေါ်လာ 2၊ 3၊ 7 နှင့် 5 သန်းရှိသည်။ ဒေတာ၏ ပျမ်းမျှသွေဖည်မှုကား အဘယ်နည်း။

ပထမဦးစွာ ကျွန်ုပ်တို့သည် ဒေတာကို ပျမ်းမျှထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် စုစုပေါင်းလေ့လာသုံးသပ်ချက် (၄) ခုဖြင့် ပေါင်းပြီး ပိုင်းခြားပါသည်။

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

ကျွန်ုပ်တို့သည် ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် ပျမ်းမျှသွေဖည်သော ဖော်မြူလာကို အသုံးပြုသည်-

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

ကျွန်ုပ်တို့သည် ဒေတာကို ဖော်မြူလာအဖြစ် အစားထိုးသည်-

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

ကျွန်ုပ်တို့သည် ပိုင်းဝေတွင် တွက်ချက်မှုများ ပြုလုပ်သည်-

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

နောက်ဆုံးအနေနှင့်၊ နမူနာ၏ပျမ်းမျှသွေဖည်မှုကိုရရှိရန် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားပါသည်။

$D_{\overline{x}}=1,75$

ပျမ်းမျှ Deviation ဂဏန်းတွက်စက်

၎င်း၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်အစုတစ်စုကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာအတွက် ပျမ်းမျှသွေဖည်ခြင်း။

ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာများ၏ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်ရန်၊ အောက်ပါအဆင့်များကို လိုက်နာရပါမည်။

ကိန်းဂဏန်းအချက်အလက်အစုံ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို ဆုံးဖြတ်ပါ။ ဒေတာကို အုပ်စုဖွဲ့ထားသောကြောင့်၊ ပျမ်းမျှတွက်ချက်ရန် စကားရပ်မှာ-

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

အတန်းအဆင့်နှင့် ပျမ်းမျှအကြားခြားနားချက်၏ ပကတိတန်ဖိုးနှင့် ညီမျှသည့် ကြားကာလတစ်ခုစီ၏ သွေဖည်မှုကို တွက်ချက်ပါ။

$|x_i-\overline{x}|$

ကြားကာလတစ်ခုစီ၏ သွေဖည်မှုကို ၎င်း၏ ပကတိကြိမ်နှုန်းဖြင့် မြှောက်ပါ။

$|x_i-\overline{x}|\cdot f_i$

ယခင်အဆင့်မှ ရလဒ်အားလုံးကို ပေါင်းထည့်ပြီးနောက် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းပါ။ ရရှိသောရလဒ်မှာ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော နမူနာ၏ ပျမ်းမျှသွေဖည်မှုဖြစ်သည်။

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

နိဂုံးချုပ်အားဖြင့်၊ အုပ်စုဖွဲ့ဒေတာမှ ပျမ်းမျှသွေဖည်မှုရရှိရန် ဖော်မြူလာ မှာ-

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

ဒေတာကို အုပ်စုဖွဲ့သောအခါတွင် ဒေတာများစွာရှိနေသည်ဟု ဆိုလိုပြီး ပျမ်းမျှသွေဖည်မှုကို ရှာဖွေရာတွင် အဆင့်များစွာပါဝင်ပါသည်။ ထို့ကြောင့် ကြိမ်နှုန်းဇယားများကို တွက်ချက်ရာတွင် အများအားဖြင့် အသုံးပြုကြသည်။

ဒေတာများကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့်အခါ ပျမ်းမျှသွေဖည်မှုကို တွက်ချက်နည်း အောက်တွင် အဆင့်ဆင့် လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။

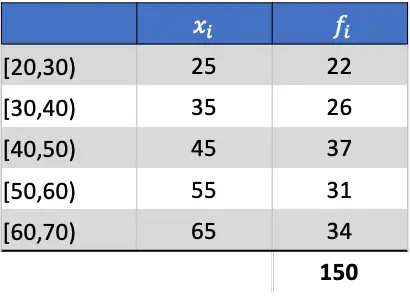
ပထမဆုံးလုပ်ရမည့်အချက်မှာ အုပ်စုဖွဲ့ထားသောဒေတာ၏ ပျမ်းမျှအား တွက်ချက်ရန်ဖြစ်သည်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် အတန်းမှတ်စုကို ၎င်း၏ကြိမ်နှုန်းဖြင့် မြှောက်ခြင်းဖြင့် ဇယားထဲသို့ ကော်လံတစ်ခုကို ပေါင်းထည့်သည်-

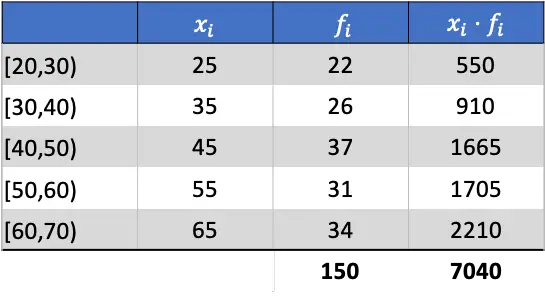
ထို့ကြောင့် ဂဏန်းသင်္ချာဆိုလိုရင်းသည် ပေါင်းထည့်ထားသော ကော်လံ၏ ပေါင်းလဒ်ကို ပကတိကြိမ်နှုန်းများ၏ ပေါင်းလဒ်ဖြင့် ပိုင်းခြားခြင်း၏ ရလဒ်ဖြစ်သည်-

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

ယခု ကျွန်ုပ်တို့သည် ဒေတာ၏ ဆိုလိုရင်းကို သိရှိပြီး ပျမ်းမျှသွေဖည်မှုကို ရှာဖွေရန် လိုအပ်သောကော်လံများအားလုံးကို ထည့်နိုင်သည်-

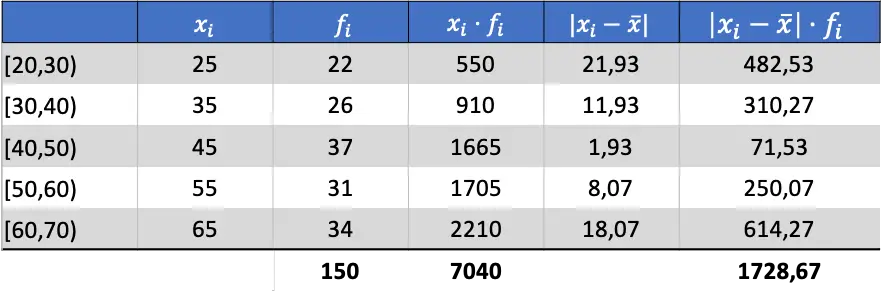
ထို့ကြောင့်၊ ပျမ်းမျှသွေဖည်မှုရရှိရန် နောက်ဆုံးကော်လံ၏ပေါင်းလဒ်ကို လေ့လာသုံးသပ်ချက်စုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။